二阶控制系统的Multisim建模与仿真
邵桂荣
(运城学院物理与电子工程系,山西运城044000)
二阶控制系统的Multisim建模与仿真
邵桂荣
(运城学院物理与电子工程系,山西运城044000)
针对现有基于Matlab的自动控制原理实验存在的建模、编程难,硬件电路缺乏等缺点,以典型二阶控制系统为例,采用Multisim12设计其硬件实现电路,推导出传递函数及系统处于不同阻尼状态下参数的取值范围。仿真分析了阶跃响应、频率响应及开环对数频率特性,并得到了较为形象、准确的实验结果。该实验过程即接近实际操作效果,又具有仿真的优点,有助于培养学生设计、调试系统的能力。
二阶控制系统;Multisim;时域;频域
运城学院“自动控制原理”课程实验采用Matlab进行仿真。该传统实验方法存在的不足有:①该方法以数学模型为基础,学生很难了解实际控制系统所涉及的各个环节;②部分学生理论知识欠缺,很难建立正确的数学模型;③部分学生编写程序困难。
基于此,在传统方法的基础上,采用Multi⁃sim12进行硬件模拟实验,充分利用Multisim元器件库中的元件(如集成运放、电阻、电容等)建立控制系统的硬件模拟电路,采用虚拟仪器(如示波器、波特图仪)等观察实验波形,进而分析实验结果[1]。以二阶控制系统为例进行说明。
1 二阶系统的数学模型
二阶系统的典型结构如图1所示[2]。
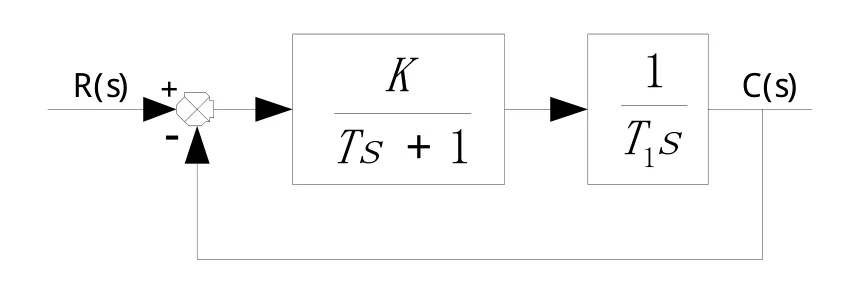
图1 二阶系统动态结构图
闭环传递函数为:

闭环特征方程为:

当ξ=0时,二阶系统有一对共轭虚根S1,2=±jωn,系统处于无阻尼状态;当0<ξ<1时,二阶系统有一对共轭复根,系统处于欠阻尼状态;当ξ=1时,二阶系统有一对相等的负实根S1,2=-ωn,系统处于临界阻尼状态;当ξ>1时,二阶系统有两个不同的负实数根,系统处于过阻尼状态。
2 二阶系统的Multisim建模
在Multisim12仿真环境中,建立二阶系统模拟电路如图2所示[3]。

图2 二阶系统Multisim建模图
当开关S1A闭合,U2、C1、R3、R4构成惯性环节,U3、C2、R5构成积分环节。利用复数阻抗法计算各环节的传递函数,经推导得系统的传递函数为:

二阶系统特征参数为:

经计算得:当开关S1A闭合,R4=50 K时,ξ=1;当0<R4<50 K时,ξ>1;当R4>50 K,0<ξ<1。当开关S1A断开,此时ξ=0。
3 二阶系统时域仿真分析
线性控制系统的时域分析具有直观、准确的优点,可以提供系统时间响应的全部信息。时域分析中常用到的输入信号有阶跃、斜坡、加速度及脉冲信号[4]。如图2中,输入采用直流电源V1和开关J1模拟单位阶跃输入信号,电源V1参数值为1V,开关J1的TON时间设为0.1 s[5],输出采用示波器来观测,仿真结果如图3所示。


图3 二阶系统的阶跃响应
从图3中可知:S1A断开,系统处于无阻尼状态,阶跃响应为等幅正弦振荡曲线。S1A闭合,R4为50 K时,系统处于临界阻尼状态,阶跃响应为单调上升的曲线;R4为450 K和200 K时,系统处于欠阻尼状态,阶跃响应为衰减振荡曲线,且R4阻值越大,振荡越厉害;R4为25 K和10 K时,系统处于过阻尼状态,阶跃响应为单调上升曲线,且R4值越大,达到稳态值的时间越短。
4 二阶系统频域仿真分析
4.1 频率响应仿真分析
频率响应是控制系统对正弦输入信号的稳态响应。一个稳定的线性系统,在正弦信号的作用下,稳态输出仍是一个与输入同频率的正弦信号,且输出的幅值与相位是输入正弦信号频率的函数。如图2中,输入采用幅值的有效值为1V,频率为50 Hz的正弦信号[6],示波器A通道为输入信号,B通道为输出信号,仿真结果如图4所示。

图4 二阶系统频率响应
从图4中可知:R4取不同值时,频率响应与输入信号的频率相同,且均滞后于输入信号。R4=400 K时,频率响应与输入信号的幅值比为0.11,频率响应滞后于输入信号170°;R4=10 K时,频率响应与输入信号的幅值比为0.01,频率响应滞后于输入信号98°。
4.2 开环对数频率特性仿真分析
将图2中的示波器用Bode Plotter代替[7],测量二阶开环系统的对数幅频特性与对数相频特性,IN接电路的输入端,OUT接电路的输出端。仿真结果如图5所示。
从图5中可知:R4取不同值时,对数相频特性曲线变化范围相同,对数幅频特性曲线在低频段与高频段对应斜率相同,且在转折频率处斜率均发生了变化。R4=300 K时,转折频率在4.79~7.85 Hz范围内,即30.1~49.3 rad/sec;R4=20 K时,转折频率在47.29~94.1 Hz范围内;均与理论计算值吻合。

图5 二阶系统开环对数频率特性
5 结论
本文以二阶系统为例,介绍了Multisim硬件模拟电路的建立方法,分析了二阶系统的时域、频域响应及频率特性,仿真结果与理论分析一致。采用Multi⁃sim进行建模仿真,有效结合了传统实验箱与Matlab仿真的优点,是我校拓宽实践教学方法的一种手段,意在逐步加强学生对理论知识的理解及应用。
[1]郭锁利,刘延飞.Multisim的电子系统设计、仿真与综合应用[M].北京:人民邮电出版社,2015.
[2]胡寿松.自动控制原理[M].北京:科学出版社,2001.
[3]陈俊英.基于Multisim的“自动控制原理”课程仿真实验研究[J].实验室科学,2012,15(3):120-122.
[4]孟庆明.自动控制原理[M].北京:高等教育出版社,2008.
[5]罗旭.Matlab和Multisim软件在教学中的应用[J].广东农工商职业技术学院学报,2010,26(2):79-81.
[6]李琳芳,刘艳畅,崔微微.基于Multisim与Matlab的二阶系统响应分析与仿真[J].河南科技学院学报,2015,43(4):59-63.
[7]黄智伟.基于NI Multisim的电子电路计算机仿真设计与分析[M].北京:电子工业出版社,2015.
Multisim Modeling and Simulation of Second-order Control System
SHAO Gui-rong
(Department of Physics and Electronics Engineering,Yuncheng University,Yuncheng Shanxi,044000)
For the faults of the existing Automatic Control Principle’s experiments,such as modeling and programming difficulty and the lack of hardware circuit.The paper designs the hardware circuit of typical second-order control system using Multisim12,the transfer function are deduced and parameters’value scope are calculated based on different damping state.Step and Frequency re⁃sponse and open-loop logarithmic frequency characteristics are simulated.At last,visual and accurate experimental results are ob⁃tained.The experiment process is close to the actual operation effect and has the advantages of the simulation.The Multisim can help to cultivate students’ability about designing and debugging system.
second-order control system;multisim;time domain;frequency domain
TP1
A
1674-0874(2016)05-0031-03
2016-07-15
山西省教育厅重点教学研究改革项目[J2014104]
邵桂荣(1979-),女,山西运城人,副教授,研究方向:电力电子、自动控制课程的教学及研究。
〔责任编辑 高彩云〕

