矩阵相似在微分方程组中的应用

张海涛

（山西大同大学数学与计算机科学学院，山西大同037009）

矩阵相似在微分方程组中的应用

张海涛

（山西大同大学数学与计算机科学学院，山西大同037009）

在高等代数的研究范围内，计算矩阵的特征值与特征向量是一个基本问题。矩阵的相似性会关系到特征值与特征向量的计算,同时也会关系到矩阵对角化问题。主要探讨了矩阵的相似在微分方程组中的应用。

矩阵相似；特征向量；特征多项式；微分方程组

1 矩阵相似的定义及有关性质

1.1 矩阵相似的定义

定义1设B，D为数域P上两个m级矩阵，假如能找到数域P上的m级可逆矩阵X，使得D=X-1BX，就说B相似于D，记作B～D[1-4]。

1.2 矩阵相似的性质

矩阵相似的基本性质：

自反性：A～A。这是因为A=E-1AE;

对称性：A～B则B～A。如果A～B，从而有可逆矩阵X，使B=X-1AX。令Y=X-1,那么有A=XBX-1=Y-1BY，所以B～A;

传递性：A～B及B～C,那么可以得到A～C。已知有X，Y使得B=X-1AX，C=Y-1BY。令Z=XY，就有C=Z-1AZ，因此A～C。

2 矩阵相似在微分方程组中的应用

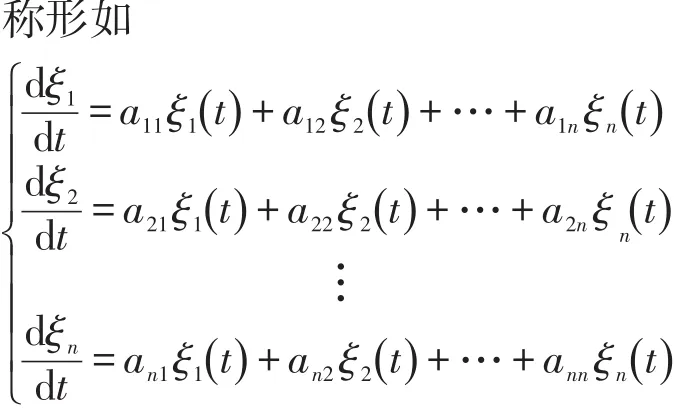
的方程组为常系数线性齐次微分方程组，简称微分方程组，其中ξi=ξi(t)(i=1,2,…,n)是自变量t的函数，aij(i,j=1,2,…,n)是复数。

若矩阵A相似于一个对角矩阵

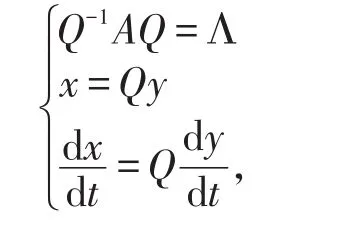
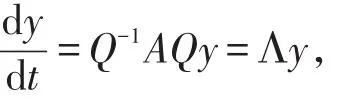
那么（1）可简化为下列形式：

从而简化了问题的求解。

例1解微分方程组

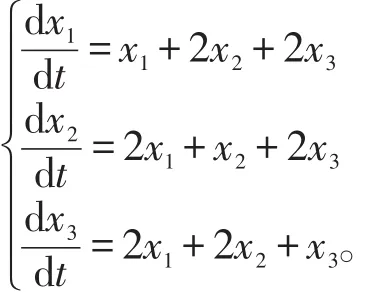
矩阵A的特征多项式,矩阵A的特征值为λ1=5,λ2=λ3=-1，对应于λ1=5的特征向量为,而对应于二重特征根λ2=λ3=-1，有两个线性无关的特征向量，故A可对角化。则存在可逆矩阵,使得=Λ。

其中y=(y1,y2,y3)T，则，代入式（1）得，即，写成分量形式有，，解出

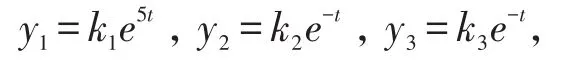
故由（3）得原方程组的解x1=k1e5t-k2e-t-k3e-t，

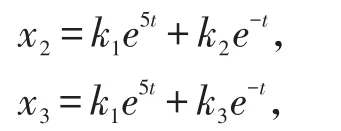
式中ki(i=1,2,3)为任意常数。

例2解线性微分方程组

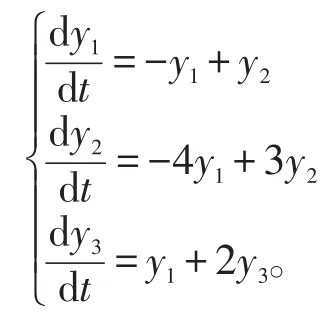
解方程组右边的系数矩阵为

A的特征多项式

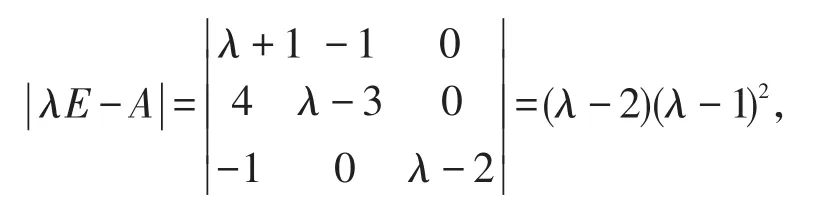
由此必然存在一个非奇异矩阵C和若当矩阵J，使得

现在求非奇异矩阵C，设C=(x1,x2,x3)。由于λ1=2，λ2=1分别为单特征值和二重特征值，所以有

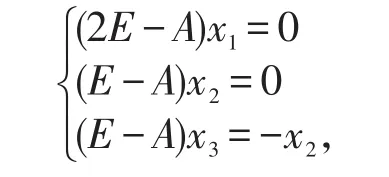
因此可知x1和x2为对应于两个相异特征值2和1的特征向量，且，而x3是广义特征向量，故非奇异矩阵C为：可得到故可以做变换y=Cz，，则由可以得到，即，那么上面的方程的坐标写法为:，。

显然可以直接解得z1=k1e2t，z3=k3et,那么也就可以得到z2=et(k3t+k2)，再由y=Cz，即得y1=et(k3t+k2)，y2=et(2k3t+2k2+k3)，y3=k1e2t-et(k3t+k2+k3),式中ki(i=1,2,3)为任意常数。

文中探讨了矩阵的相似在微分方程组中的应用，矩阵相似的特性使其应用范围十分广泛，文中主要将矩阵相似与可对角化矩阵、若当标准型矩阵紧密联系起来，简化了很多问题的求解。

[1]刘嘉.矩阵相似及其应用[J].中国西部科技,2010,9（26):46-48.

[2]王萼芳,石生明.高等代数（第三版）[M].北京：高等教育出版社,2003:288-325.

[3]崔文君.矩阵相似的相关研究[J].科技致富向导,2013(15）:32.

[4]谢启鸿.秩在矩阵相似中的应用[J].高等数学教育,2012,15(1):30-32.

The Application of Similar Matrix in System of Differential Equations

ZHANG Hai-tao
(School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009)

Within the scope of the study of Higher Algebra,computing matrix’s eigenvalue and eigenvector is a basic problem.The similarity of matrix is related to the calculation about eigenvalues and eigenvectors,and it is also closely linked to the diagonaliza⁃tion of matrix.This paper mainly discusses the similarity of matrices and its applications in system of differential equations.

similar;eigenvector;characteristic polynomial;system of differential equations

175.14

A

1674-0874(2016)05-0005-02

2016-07-08

张海涛（1974-），女，山西阳高人，硕士，副教授，研究方向：常微分方程。

〔责任编辑 高海〕