时间模上四-点边值问题两个正解的存在性

乔世东

(山西大同大学数学与计算机科学学院，山西大同037009)

时间模上四-点边值问题两个正解的存在性

乔世东

(山西大同大学数学与计算机科学学院，山西大同037009)

多点边值问题至少有一个正解的存在性已经解决，讨论多点边值问题至少有两个正解的存在性。

边值问题；正解；时间模；锥；不动点定理

边值问题（1）至少有一个正解[1]的存在性已经给出。本文讨论

至少有两个正解的存在性。其中T是一个时间模,

（A1）q∈Crd([0,1],[0,∞))且存在t0∈[0,1]，使得q(t0)＞0;

（A2）f:(0,∞)⊂T→[0,∞)是连续的且f(y)＞0;

首先我们给出几个引理。这些引理基于下面的边值问题

引理1设条件（A1）成立,则y(t)是方程（2）的唯一解

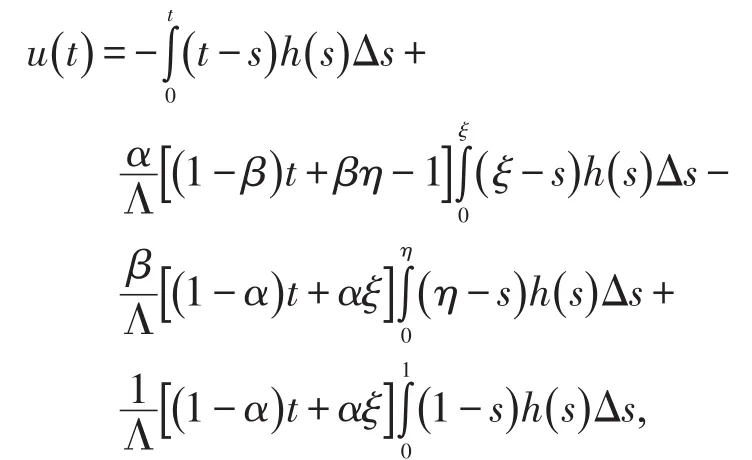
这里，Λ=αξ(1-β)t+(1-α)(1-βη)。

证明 由uΔΔ(t)+h(t)=0,

利用边值条件,有

引理2设条件（A1）、（A2）成立,则y(t)是方程（2）的解u(t)满足u(t)≥0,t∈[0,1]⊂T。

证明 事实上，uΔΔ(t)=-h(t)≤0，显然有u(t)在t∈[0,1]⊂T是凸的，因此，分以下三种情况证明。

情况（1）若min{u(0),u(1)}≥0，由u(t)的凸性知道，u(t)≥(1-t)u(0)+tu(1)≥0，t∈[0,1]⊂T；

情况（2）若min{u(0),u(1)}＜0≤max{u(0),u(1)}，

设u(0)=min{u(0),u(1)}＜0，

则u(1)=max{u(0),u(1)}≥0，且u(ξ)＜0。

由u(t)的凸性知道，u(ξ)≥(1-ξ)u(0)+ξu(1)=α(1-ξ)u(ξ)+βξu(1),u(ξ)≥(1)≥0，矛盾。

如果u(1)=min{u(0),u(1)}＜0，

则u(0)=max{u(0),u(1)}≥0，且u(η)＜0。由u(t)的凸性知道，u(η)≥(1-η)u(0)+ηu(1)=(1-η)u(0)+βηu(η),所以，u(η)≥(0)≥0，矛盾；

情况（3）若max{u(0),u(1)}＜0，则u(ξ)＜0，u(η)＜0。由u(t)的凸性知道，u(ξ)≥(1-ξ)u(0)+ξu(1)=α(1-ξ)u(ξ)+βξu(1)和u(η)≥(1-η)u(0)+ηu(1)=(1-η)u(0)+βηu(η)有

记E=Crd[0,1]为一个B-空间，，锥P⊂E,

边值问题(1)有解u=u(t)当且仅当u是下列算子方程的解。

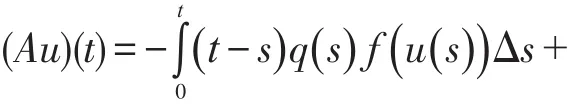
引理3设u∈P,则

u(t)≥(1-t)‖u‖,t∈[0,1]⊂T，

其中‖u‖=|u(t)|。

证明因为u(t)在t∈[0,1]⊂T上非负的和减少的，因此有u(0)≥u(t)≥u(1)，在t∈[0,1]⊂T。从而。

由（4）和（5）知u(t)≥(1-t)‖u‖,t∈[0,1]⊂T。

证毕。

定理1(Avery-Henderson[2-3])设P是实巴拿赫空间E的一个锥,集合

P(Φ,r)={u∈P:Φ(u)＜r}。

如果η,Φ是定义在P上的增加的,非负的连续函数,让θ是一个定义在P上非负的连续函数且有θ(0)=0满足对一些正的常数r,M及所有的,Φ(u)≤θ(u)≤γ(u),‖u‖≤MΦ(u)。又假设存在常数0＜p＜q＜r满足下列条件,θ(λu)≤λθ(u),0≤λ≤1,u∈∂P(θ,q)。假设A:P是P上的一个全连续算子满足下列条件:

（1）Φ(Au)＞r对所有的u∈∂P(Φ,r)；

（2）θ(Au)＜q对所有的u∈∂P(θ,q)；

（3）P(γ,p)≠φ和γ(Au)＞p对所有的u∈∂P(γ,p)。

则A至少有两个不动点u1,u2,满足p＜γ(u1),θ(u1)＜q和q＜θ(u2),Φ(u2)＜r。

定义非负连续增函数Φ,θ,γ满足

对每一个u∈P,有Φ(u)=θ(u)≤γ(u)。另外,对每一个u∈P,由引理3知Φ(u)=u(η)≥(1-η)‖u‖。

同样0≤λ≤1,有θ(λu)≤λθ(u)，u∈∂P(θ,q)。记

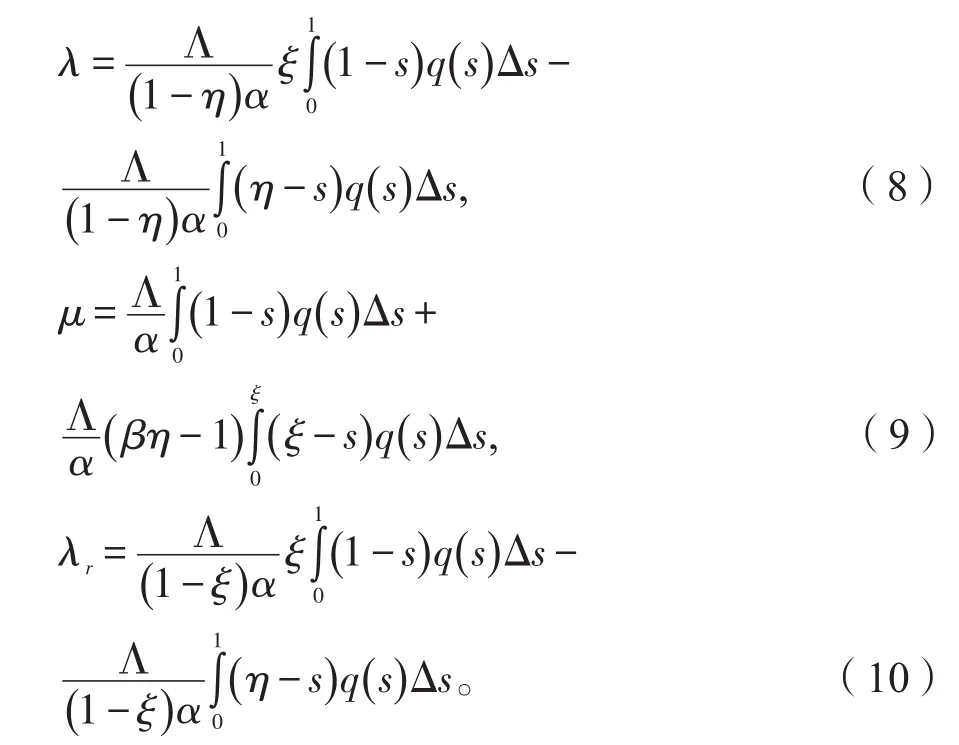
定理2设条件(A1)～(A2)成立,又设存在常数,满足:

则边值问题(1)至少有两个正解u1,u2,满足γ(u1)＞p,θ(u1)＜q,和q＜θ(u2),Φ(u2)＜r。

证明验证定理1的所有条件都满足。

定义一个全连续积分算子A:P→E满足:

其中u∈P,t∈[0,1]⊂T,.对于u∈P,t∈[0,1]⊂T,.易知(Au)(t)满足方程(1)。令u∈∂P(Φ,r)满足。

由假设条件(c1)知。

因为Au∈P，由引理3得到

设u∈∂P(θ,q),则

由假设条件(c2)知

故定理1的条件（2）满足。

定义u(t)=，t∈[0,1]⊂T，则γ(t)=＜p，所以，P(γ,p)≠φ。

令u∈∂P(γ,p),则γ(u)==u(ξ)=p，0≤u(t)≤p，t∈[ξ,1]⊂T,由假设条件(c3)知f(u(t))＞,t∈[ξ,1]⊂T。

又因为Au∈P，由引理3得到

因此(1)至少有两个正解u1,u2,满足γ(u1)＞p,θ(u1)＜q,和q＜θ(u2),Φ(u2)＜r。

[1]乔世东，张英.时间模上四-点边值问题正解的存在性[J].山西大同大学学报(自然科学版)，2014,30（3）：1-3.

[2]AVERY R I,HENDERSON J.Two positive Fixed Points of Nonlinear Operators on Ordered Banach spaces[J].Comm Appl Nonlin⁃ear Anal,2001（8）:27-36.

[3]乔世东，张英.时间模上非线性两-点边值问题的研究[J].山西大同大学学报(自然科学版)，2010，26(2):1-3.

Existence of Two Positive Solutions to a Four-point Boundary Value Problems on Time Scales

QIAO Shi-dong
(School of Mathematics and Computer Sciences,Shanxi Datong University,Datong Shanxi，037009)

Some results are obtained for the existence of at least one positive solutions of theabove problem by using fixed point theorem.In this paper,we study the existence of at least two positive solutions of a nonlinear boundary value problem.

boundary value problem;positive solution;time scales;cone;fixed point theorem

175.14

A

1674-0874(2016)05-0001-04

2015-12-08

乔世东(1963-)，男，山西左云人，硕士，教授，研究方向：代数与方程。

〔责任编辑 高海〕