基于相平面方法的车辆稳定性控制

柳　江， 陈　朋， 李道飞

(1.青岛理工大学 汽车与交通学院， 山东 青岛 266520；2.浙江大学 动力机械及车辆工程研究所， 浙江 杭州 310027)



基于相平面方法的车辆稳定性控制

柳江1， 陈朋1， 李道飞2

(1.青岛理工大学 汽车与交通学院， 山东 青岛 266520；2.浙江大学 动力机械及车辆工程研究所， 浙江 杭州 310027)

相平面方法； 边界函数； 稳定性； 横摆力矩控制

1　车辆模型的建立

1.1整车模型

针对某紧凑型轿车，建立二自由度扩展的整车模型，如图1所示.忽略空气阻力以及转向系统和悬架系统的影响，考虑4个车轮在非线性域内的侧偏角和垂直载荷的变化，分别计算各个轮胎的侧向力．

图1　整车模型Fig.1　The vehicle model

由整车模型可以得到系统运动方程：

(1)

(2)

β=arctan(v/u).

(3)

各个轮胎的侧偏角如下：

(4)

(5)

(6)

(7)

为了研究轮胎非线性，考虑到载荷的转移，4个轮胎的垂直载荷分别是：

(8)

(9)

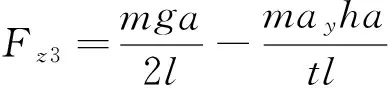
(10)

(11)

式(1)至式(11)中：δ是前轮转角，u是整车的纵向速度，v是整车的侧向速度，β是质心侧偏角，r是横摆角速度，αi(i=1，2，3，4)分别是4个轮胎的侧偏角，Fyi(i=1，2，3，4)分别是4个轮胎的侧向力，整车的其他参数如表1．

表1　整车的部分参数

1.2轮胎模型

由于稳定性控制是在轮胎的非线性区域内发生，需要对轮胎实际的侧向力进行拟合.考虑轮胎力的有效性和计算的简洁性，采用简化的MF公式进行拟合[6]．

轮胎侧向力由下式给出：

Fy=μFzsin(Darctan(Bαi))，

(12)

式中：Fy是轮胎的侧向力，μ是路面的附着系数，Fz是轮胎的垂直载荷，B和D是待拟合系数.拟合结果如图2．

图2　不同垂直载荷下轮胎侧向力的拟合Fig.2　The fitting of tire lateral force at different vertical loads

在μ=1时，通过对不同垂直载荷下轮胎侧向力的拟合，发现随着轮胎侧偏角的变化，可得到公式(12)的拟合系数：B=1.438，D=0.210 8．

拟合的轮胎侧向力最大偏差为2%，但是经过估算，单个轮胎的主要垂直载荷工作区域是在5 000 N之内，所以通过拟合而得到的参数能够满足相平面的要求．

2　相平面边界

由于路面附着系数和车速对相平面的边界影响很大，故需计算不同车速和路面附着系数下的稳定性边界，再根据此结果拟合出能够随着车速和路面附着系数变化的边界函数．

2.1相平面稳定边界

所建立的整车模型方程可以表示为公式(13)和(14)所示的二阶自治系统：

(13)

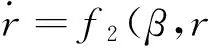
(14)

图相平面图Fig.

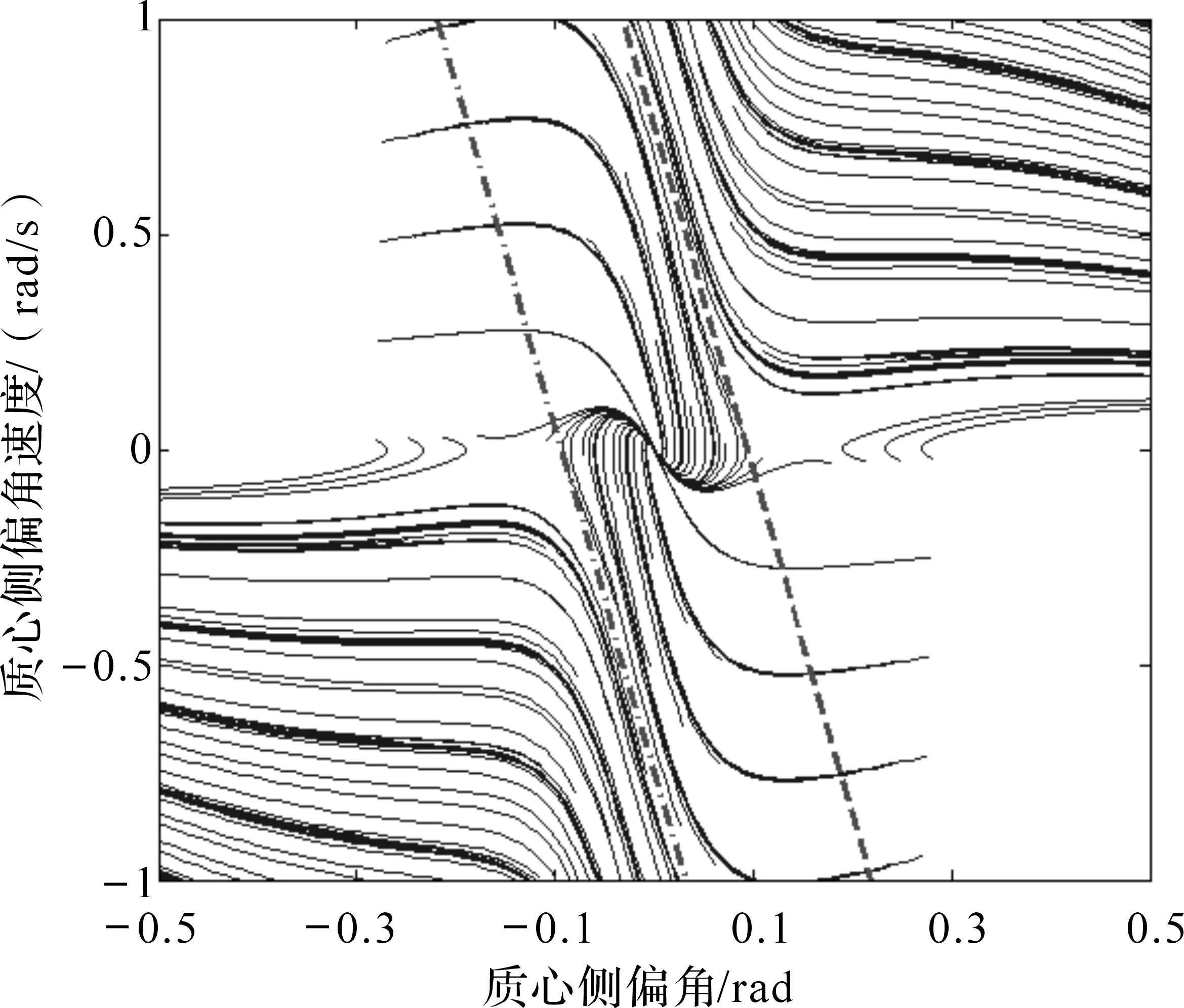
图相平面图稳定区域Fig. phase plane with stability region

通过观察图3相平面的轨迹线变化，根据能回到稳定相点(0，0)的轨迹线划分稳定区域，划分的相平面稳定区域为图5中的2条对称虚直线包围的区域，这2条虚直线可以用方程(15)表示：

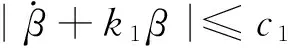
(15)

式中k1，c1为边界系数．

类似地，根据图4能够回到原点的相轨迹，用2条对称的双折线划分稳定区域，如图6中的虚线所示，并可用方程(16)和(17)同时表示：

|r+k2β|≤c2，

(16)

|r|≤c3，

(17)

式中k2，c2和c3都是此稳定域的边界系数．

图6　β-r相平面图稳定区域Fig.6　β-r phase plane with stability region

2.2不同路面附着系数的影响

整车速度u0不变时，通过改变附着系数，获得2种相平面的稳定边界的参数，获得的数据对应表2和表3．

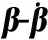
序号μk1c110.11.00.0820.22.40.1830.34.00.2240.45.00.2850.55.50.4060.66.60.4570.77.50.5580.88.00.6590.98.50.70101.09.80.85

表3不同路面附着系数下β-r相平面的边界参数

Table 3Boundary parameters ofβ-rphase plane under different road friction coefficients

序号μk2c2c310.10.70.080.021220.21.30.150.042430.32.00.250.063640.42.20.320.084850.52.70.420.106960.63.00.490.127170.73.80.500.148380.84.10.600.169590.94.50.700.1907101.05.00.800.2119

运用多项式拟合表2的数据，得到拟合公式(18)和(19)：

k1=-4.28μ2+13.83μ-0.1283，

(18)

c1=0.2197μ2+0.5814μ+0.03167.

(19)

拟合表3中的数据，得到拟合公式 (20)，(21)和(22)：

k2=4.618μ+0.38，

(20)

c2=0.757μ+0.0107，

(21)

c3=0.212μ.

(22)

2.3不同车速的影响

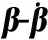
序号u/(km/h)k1c11608.050.752708.050.763808.010.754908.010.7751008.000.7561107.950.7671208.020.7481308.000.7491408.010.76101508.000.76

表5不同车速下β-r相平面的边界参数

Table 5Boundary parameters ofβ-rphase plane under different vehicle speeds

序号u/(km/h)k2c2c31605.01.00.28252704.80.900.24223804.50.800.21194904.30.700.188451004.10.600.169561103.90.550.154171203.70.560.141381303.50.500.130491403.00.450.1211101502.80.400.1130

从图表5可知，车速u与3个参数成反比关系，通过数据得到边界参数的拟合公式(23)，(24)和(25)：

(23)

(24)

(25)

2.4边界函数

β-r相平面边界方程的参数与μ成正比关系，而与车速成反比关系，通过路面附着系数和车速拟合的方程，可以得到β-r相平面的边界函数：

(27)

3　车辆主动稳定性控制器的设计

图7　车辆稳定性控制系统架构Fig.7　Framework of vehicle stability control system

对图5相平面中划分的稳定性区域进行处理，如图8．

图相图误差的计算Fig.8　Calculation of phase plane error

由图8得到相平面的误差计算公式：

(28)

(29)

(30)

运用PID控制算法得到横摆力矩：

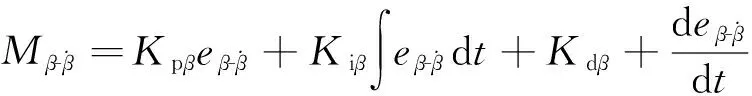
(31)

3.2基于β-r相平面的横摆力矩的计算

对图6相平面划分的稳定区域进行处理，得到简化的相平面图边界，如图9．

图9　β-r相图误差的计算Fig.9　Calculation of β-r phase plane error

通过图9获得β-r相平面的误差eβ-r：

e1=|r|-c3，

(32)

(33)

eβ-r=min(e1，e2)，

(34)

式中：e1是不稳定相点到水平线的距离且e1≥0，e2是不稳定相点到斜线的距离且e2≥0．

运用PID控制算法得到β-r相平面图的横摆力矩如下：

(35)

式中：Kpr是β-r相平面比例参数，Kir是积分的参数，Kdr是微分的参数．

3.3期望的横摆力矩的计算

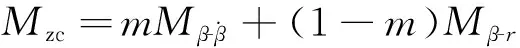
(36)

图10　分配系数m的变化Fig.10　Change of distribution coefficient m

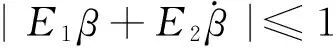
(37)

式中：

E1=1/c1，

(38)

E2=k1/c1.

(39)

4　仿真验证

图11　方向盘转角的输入Fig.11　Input of steer wheel angle

图12　质心侧偏角的变化Fig.12　Changes of vehicle sideslip angle

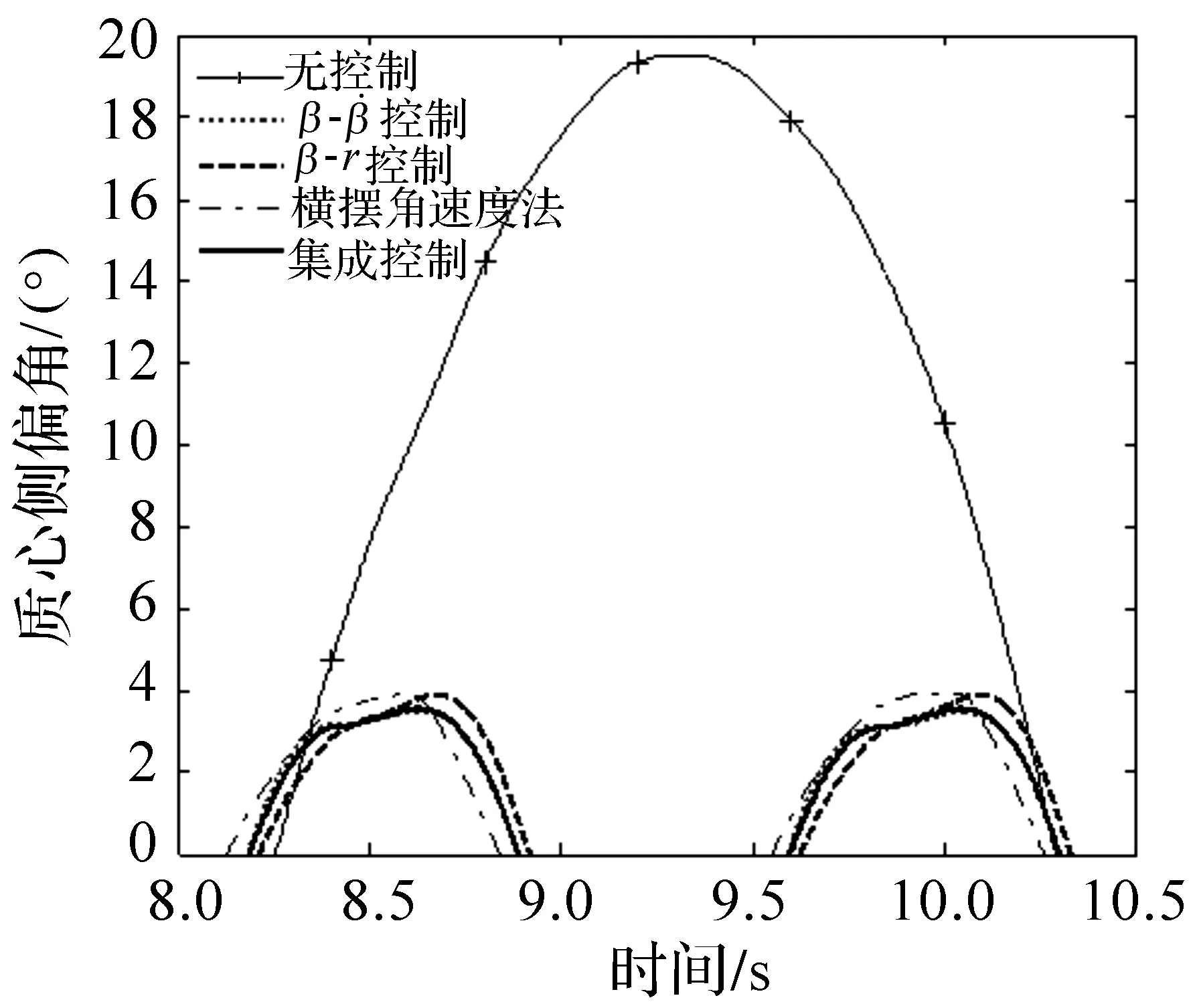
图13　图12中A区域放大图Fig.13　The enlarged drawing of A area in figure 12

图14　横摆角速度的变化Fig.14　Changes of yaw rate

图15　图14中B区域放大图Fig.15　The enlarged drawing of B area in figure 14

图16　分配系数m的变化Fig.16　The change of contribution coefficient m

图17　不同控制策略下相平面图相轨迹对比Fig.17　Comparison of phase trajectory for phase plane under different control strategies

图18　不同控制策略下β-r相平面图相轨迹对比Fig.18　Comparison of phase trajectory for β-r phase plane under different control strategies

5　结　论

[1] Van ZANTEN A T. Bosch ESP systems: 5 years of experience[J]. SAE Technical Paper， 2002, 2000-01-1633．

[2] NAOTO O， TAKEHIRO H， OSAMU Y， et al. Brake torque sensing for enhancement of vehicle dynamics control systems[J]. SAE Technical Paper， 2007, 2007-01-0867．

[3] ZHANG Lei， LIANG Yao-yu， PAN Ning， et al. Vehicle direct yaw moment control based on tire cornering stiffness estimation[C]//Procedings of the ASME 2014 Dynamics Systems and Control Conference.San Antonio， October 22-24，2014: 2-8．

[4] 胡延平，陈无畏，刘翔宇，等.基于非线性直接横摆力矩控制的ESP研究[J].汽车工程，2013， 35(5): 424-429．

HU Yan-ping， CHEN Wu-wei， LIU Xiang-yu， et al. A study on electronic stability program based on nonlinear direct yaw-moment control[J]. Automotive Engineering， 2013， 35(5): 424-429．

[5] SAMSUNDAR J， HUSTON J. Estimating lateral stability region of a nonlinear 2 degree-of-freedom vehicle[J]. SAE Technical Paper， 1988, 981172．

[6] PACEJKA H B. Tire and vehicle dynamics[M]. Oxford: Butterworth-Heinemann，2002: 46-50．

[7] 郭孔辉.汽车操纵动力学原理[M].南京:江苏科学技术出版社，2011: 42-57．

GUO Kong-hui. Vehicle handling dynamics[M]. Nanjing: Jiangsu Science Technology Press， 2011: 42-57．

[8] GUO K. A study of a phase plane representation for identifying vehicle behavior[J]. Vehicle Ststem Dynamics， 1986， 14(1): 152-167．

[9] ONO E， HOSEO S. Bifurcation in vehicle dynamics and robust front wheel steering control[J]. IEEE Transactions on Control Systems Technology， 1998， 6(3): 412-420．

[10] SHEN Shui-wen， WANG Jun. Nonlinear dynamics and stability analysis of vehicle plane motions[J]. Vehicle System Dynamics， 2007， 45(1): 15-23.

[11] INAGAKI S， KSHIRO I， YAMAMOTO M. Analysis on vehicle stability in critical cornering using phase plane method[J]. JSAE Review， 1995， 16(2): 287-292．

[12] KEN K， MASAKI Y. Vehicle stability control in limit cornering by active brake[J]. SAE Technical Paper， 1996, 960487．

[13] HE J， CROLLA D， LEVESLEY M， et al. Coordination of active steering， driveline and braking for integrated vehicle dynamics control[J]. Proc IMechE Part D: Journal of Automobile Engineering， 2006， 220(10): 1401-1421.

[14] 张晨晨，夏群生，何乐.质心侧偏角对车辆稳定性影响的研究[J].汽车工程，2011， 33(4): 277-282．

ZHANG Chen-chen， XIA Qun-sheng， HE Le. A study on the influence of sideslip angle at mass center on vehicle stability[J]. Automotive Engineering， 2011， 33(4): 277-282．

[15] 刘伟，丁海涛，郭孔辉，等.质心侧偏角相图在车辆ESC系统稳定性控制的应用[J].北京理工大学学报，2013， 33(1): 42-46．

LIU Wei， DING Hai-tao， GUO Kong-hui， et al. Application of side-slip angle phasigram to vehicle ESC system[J]. Transactions of Beijing Institute of Technology， 2013， 33(1): 42-46.

[16] 刘飞，熊璐，邓律华，等.基于相平面法的车辆行驶稳定性判定方法[J].华南理工大学学报，2014， 42(11): 63-70．

LIU Fei， XIONG Lu， DENG Lü-hua， et al. Vehicle stability criterion based on phase plane method[J]. Journal of South China University of Technology， 2014， 42(11): 63-70．

[17] 熊璐，曲彤，冯源，等.极限工况下车辆行驶的稳定性判据[J]. 机械工程学报，2015， 51(10): 103-111．

XIONG Lu， QU Tong， FENG Yuan， et al. Stability criterion for the vehicle under critical driving situation[J]. Journal of Mechanical Engineering， 2015， 51(10): 103-111．

[18] SLOTINE JJE， LI Wei-ping. Applied nonlinear control [M]. Englewood Cliff : Prentice Hall， 1991: 1-10．

Vehicle stability control based on phase-plane method

LIU Jiang1， CHEN Peng1， LI Dao-fei2

(1.School of Automobile and Transportation， Qingdao University of Technology， Qingdao 266520， China；2.Institute of Power Machinery and Vehicle Engineering， Zhejiang University， Hangzhou 310027， China)

phase-plane method； boundary function； stability； yaw moment control

2015-10-13.

国家自然科学基金资助项目(51575288，51205345)；中央高校基本科研业务费专项资金资助项目(2015QNA4014)；浙江省教育厅项目(Y201121739)；浙江省重点科技创新团队项目(2011R50008).

柳江(1976—)，男，山东青岛人，副教授，博士，从事车辆系统动力学与车辆控制研究，E-mail:zeh@163.com.

http://orcid.org//0000-0002-2541-7131通信联系人：李道飞(1981—)，男，浙江江山人，副教授，博士，从事车辆系统动力学与车辆控制研究，E-mail: dfli@zju.edu.cn.

10.3785/j.issn. 1006-754X.2016.05.002

U 46

A

1006-754X(2016)05-0409-08

本刊网址·在线期刊：http://www.zjujournals.com/gcsjxb