机器人主操作手力反馈模型误差补偿

宋莹莹，　邳志刚，　王宏民，　聂相举

(1.黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022；2.黑龙江工程学院 电气与信息工程学院， 哈尔滨 150050)



机器人主操作手力反馈模型误差补偿

宋莹莹1，邳志刚1，王宏民1，聂相举2

(1.黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022；2.黑龙江工程学院 电气与信息工程学院， 哈尔滨 150050)

根据骨科复位手术过程中医生的动作要求和从端机器人机构特点，建立了主操作手力反馈数学模型。通过测量从端实际的反馈力和主端输入力可知，力信息在主操作端的复现值与从端反馈值之间存在一定误差。 为了尽可能的减小力反馈误差，采用三层BP神经网络学习的方法对力反馈模型误差进行补偿。为验证补偿方法的有效性，建立了力反馈实验系统，实验数据表明：经过误差补偿后，力反馈误差均值降低为0.1 N，经过补偿后的力反馈数学模型，可以进一步提高力反馈的精度。

骨科复位； 主操作手； 力反馈； 误差补偿

0　引　言

骨科复位机器人手术系统是一个复杂的机器人外科手术系统，国内外专家学者对其作了大量的研究工作。外科手术机器人系统大多采用主从式遥操作结构，即由主操作端、信息通讯环节和从端执行机构组成。

当医生对患者进行相应的手术过程中，并非是直接与人体相接触，力反馈信息通常是缺失的[1-2]。可是，力觉反馈在医疗手术操作过程中非常重要，缺少它可能对患者造成严重的不良后果。因此，提供给医生灵敏的力反馈很有必要。

在遥操作骨科复位手术过程中，医生手术动作并不复杂，而且力反馈主操作手基本上处于低速的运行模式(<40 mm/s)，故可忽略系统动能的影响，可以采用静力学的方法建立主操作手力反馈数学模型[3]。在实际的控制系统中，由于数学模型的建立过程中，忽略了机构的摩擦以及系统的动能影响[4]，所以会导致力信息在主操作手上的复现值同从端力反馈值存在误差，对应用于遥操作骨科复位手术来说需要尽可能的减少力反馈的误差[5-6]。目前，借助于各类神经网络设计的补偿环节最为普遍[7]。BP神经网络可以逼近任意的非线性映射关系，具有较好的泛化能力[8]。笔者采用BP神经网络学习的方法,用于力反馈数学模型误差补偿环节，并通过搭建的力反馈控制系统实验平台，以期提高主操作手的力反馈的精度和手术的安全性。

1　力反馈型主操作手构型

1.1遥操作骨科复位手术结构

遥操作骨科复位手术系统采用位置-力(P-F)双通道主从控制体系，在主端将主操作手的空间位姿信息经过网络通道发送到从端的复位机器人系统。同时，将从端采集的接触力信息反馈到主端，经比例缩放后在力反馈主操作手上复现该反馈力，系统结构如图1所示。

1.2力反馈型主操作手机构设计

由图1可知,主操作手的设计工程中应当充分考虑操作对象的实际情况。断骨骨折后会形成近端(靠近人体心脏的一端)和远端两个骨折段，其相应的移位方式有六种类型 ，如图2所示。

针对上述骨折移位方式，复位过程中骨折的移位通常可以分解为六个自由度的简单运动，即在标准空间坐标系内x、y和z三个坐标轴上的移位和旋转。因此,对于任何骨折情况，都可以看作是骨折远近段之间进行的六自由度简单运动的集合，而复位过程则是骨折过程的逆过程。在主端医生操作主操作手控制从端复位机器人完成对断骨复位手术，需要涉及的主要动作为拔伸牵引、旋转屈伸、提按端挤、摇摆触碰等。

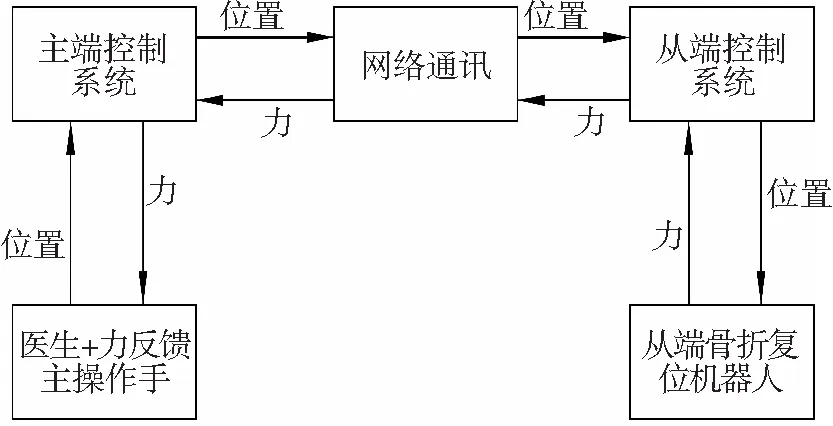
图1　遥操作骨科复位手术系统结构

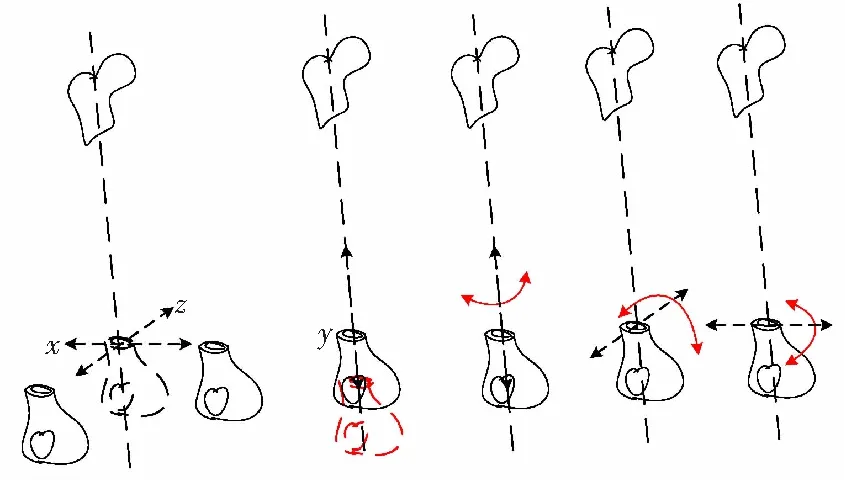
图2　骨折移位

主操作手平动机构选择与骨科复位机器人同构的并联构型，实现空间位置信息的采集，如图3a所示。采用改进的Delta机构，由上、下两个等边三角形平台及三条完全相同的支链组成。串联机构因其惯量大，将其安置在远端，用于空间姿态的调整，完成了主操作手的转动功能，实现人手腕部姿态的模拟。采用三轴汇交机构，如图3b所示。

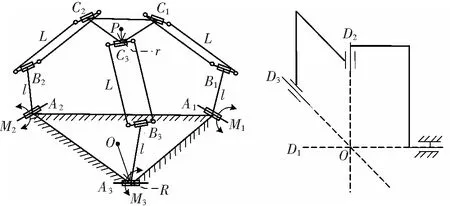
a　并联机构　　　　　　　　　　b　串联机构

2　主操作手力反馈模型

对应用于遥操作骨科复位手术的专科型力反馈主操作手而言，其操作宜人性及沉浸感是非常重要的。同时为了消除主操作手由于其自身重力对操作性能和力反馈性能的影响，有必要对主操作手的力反馈数学模型展开研究[5]。建立支链受力分析,如图4所示，支链包括主动连杆和被动连杆两部分。

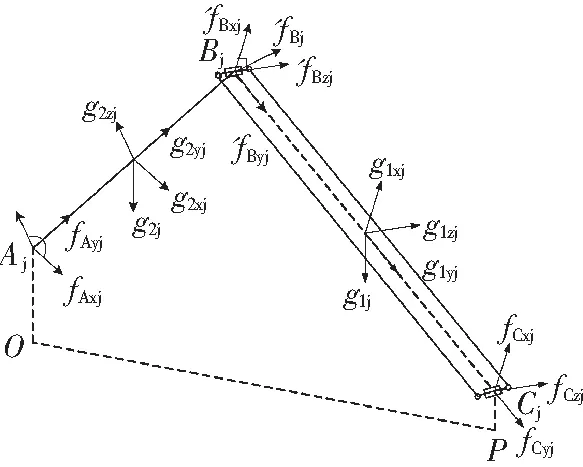
图4　主操作手支链受力分析

建立力反馈主操作手动平台中心点的力与各电机力矩之间关系：

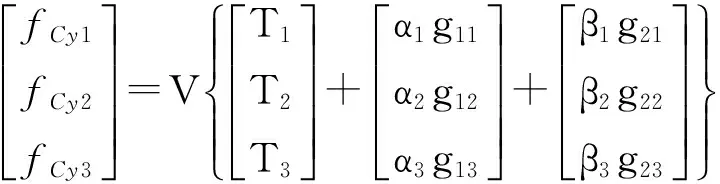
(1)

可以获得主操作手力反馈数学模型：

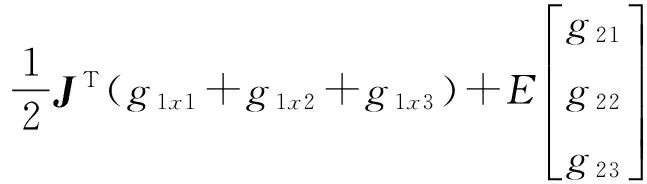
(2)

式中: g1xi——力g1j在XBj轴上的投影分量；

E——定义的中间变量；

JT——机构的力雅克比矩阵。

由式(2)可以看出,经过简化后的模型只需获取从端检测到的力、E、JT以及各杆件的重力项就可以快速计算各电机力矩值，计算的效率获得很大的提高。

利用建立的遥操作骨科复位手术系统，对比分析一组测量实际的反馈力和输入力，如图5所示，可知二者在实际系统上存在一定的误差。这主要是在数学模型的建立过程中忽略了机构的摩擦以及系统的动能影响，并对模型进行了简化，这必然会导致力信息在主操作端的复现值同从端反馈值存在一定误差，降低了骨科复位手术过程中的力反馈精度。

图5　输入力和反馈力曲线

3　BP神经网络学习的力反馈误差补偿

BP神经网络是一种单向传播的多层前向网络，一般具有三层或三层以上的神经网络，包括输入层、中间层(隐含层)和输出层。采用BP神经网络学习的方法对静力学下的力反馈数学模型进行误差校正，进一步提高力反馈精度。将式(2)进行修正：

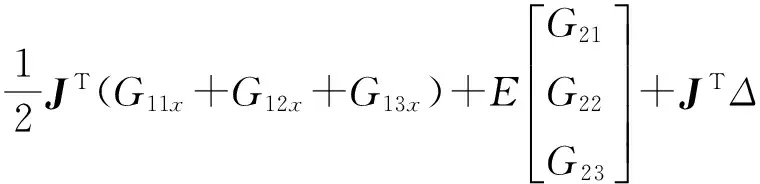
(3)

Fout=f(T),

式中:Fout——系统的输出力，可通过传感器检测获得；

T——电机输出的力矩值；

Δ——系统未知建模误差。

采用BP神经网络对Δ进行设计，选择神经网络的层数为三层，隐层和输出层的激活函数分别取为非线性Sigmoid型的tansig正切函数和线性Purelin函数。BP训练算法函数有很多种，总的来讲，基于共轭梯度法、拟牛顿算法和Levenberg-Marquardt法等数值优化算法训练函数的效率比基于启发式算法的效率要高，且基于Levenberg-Marquardt反传算法的trainlm函数具有收敛速度快的优点，故在设计中优选trainlm为训练函数，具体BP神经网络的设计过程[9]：

(1)确定输入变量P和目标变量T输入的是经过比例缩放后从端复位机器人采集的力信息，即输入的F采用值。输出的目标变量为e=Fout-F，这样只需知道Fout，就可以利用BP神经网络估计出Δ。设定BP神经网络的输入层和输出层的神经元个数都为1。

(2)确定隐层神经元个数隐层神经元个数没有明确的理论指导，在实际中只能通过对不同的神经元数进行训练比较，然后选择适当的个数。BP网络程序训练过程中采用的是训练样本中的1 400组数据。网络误差为1 400组真实值与BP网络计算值之差。通过误差比较，当误差值最小时，网络最准确，故可以确定最佳的隐层神经元个数为16。寻找最优神经元个数需要很长的训练时间，一般在一个小时左右。

(3)BP神经网络的仿真计算 利用MATLAB中的神经网络工具箱，建立好BP网络对模型进行了训练。

首先模拟手术牵引动作采集一组输入力和实际的反馈力，为了消除噪声干扰的影响，将给定输入、输出力信息利用Kalman filer滤波[10]，并经过BP神经网络学习后，给出200个测试数据的实际误差e曲线和网络学习后的误差曲线，如图6所示。

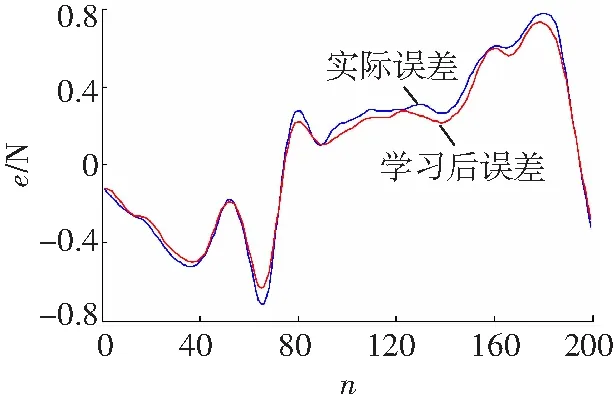
图6　力误差曲线

由图6可以看出，二者依然存在一定的偏差，但学习后的误差函数基本上能够跟踪实际误差的变化，因此将BP神经网络学习后的误差函数作为补偿添加到实际的力反馈系统中，可以进一步提高力反馈的精度。

4　主操作手力反馈实验

利用建立的力反馈数学模型并结合专科型力反馈主操作手搭建力反馈测量系统。为了测量出主操作手三维反馈力，实验中在动平台上中心点安装了ATI公司的mini45六维力传感器，如图7所示。

图7　主操作手力反馈实验平台

当医生操作主操作手时，若在自由空间运动，根据力反馈数学模型中将外力项设为零，即可得到补偿主操作手自身重力的重力补偿公式。该实验为了验证主操作手重力补偿算法的有效性，同时也可以验证误差补偿后模型算法的合理性。利用主操作手力反馈实验平台，直接测量主操作手在特定运动轨迹下人手输出力的情况，如图8所示。

图8　运动动平台输出力

Fig. 8Outputforceofmovingplatformwithleftlimbmovement

从图8可以看出，开启重力补偿的情况下末端人手克服重力所需作用力较小，误差均值在0.5 N左右。为了验证利用BP神经网络学习进行力误差补偿后算法的有效性,测量输入的外力,如图9所示。

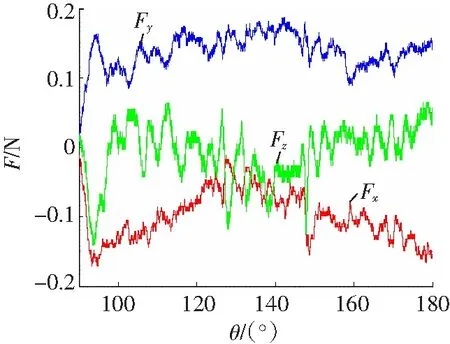
图9　误差补偿后自由空间运动所需的外力

由图9可以看出，在自由空间医生只需要输出0.13 N左右的力就可以控制主操作手在工作空间内运动，同补偿前对比减小了0.45 N左右的力。为了进一步验证在外力输入下力反馈效果，在保证重力补偿的前提下采集从端一组牵引力作为主端的输入力，并利用传感器检测动平台末端输出力的大小如图10所示，同时给出误差曲线如图11所示。

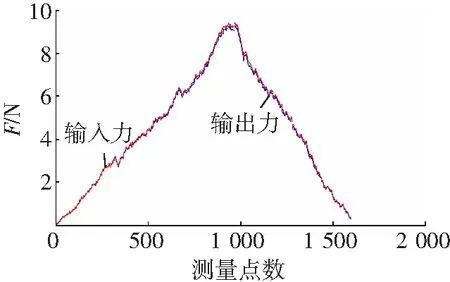
图10　误差补偿后力对比

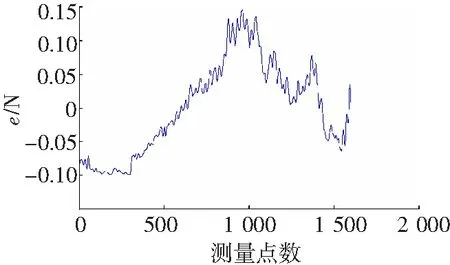
图11　力信息误差

由图10可以看出，输入的一组牵引力经过比例缩放后能够准确复现在主操作手上，使医生感受到该反馈力。图11中力的误差曲线分析可知二者误差较小，误差最大值不超过0.15 N，是符合医疗手术要求的。经过校正后的力反馈模型提升了力反馈精度，进一步保证了手术的顺利完成。

5　结束语

BP神经网络学习方法可以实现对力反馈模型误差的补偿。 在遥操作骨科复位手术的过程中，为了消除主操作手自身重力对操作者带来的疲劳感和弥补对从端接触力的缺失，根据骨科复位手术的特点，建立了基于主操作手力反馈数学模型。为了降低模型等效和机构简化对力反馈精度的影响，采用BP神经网络学习的方法对力反馈误差进行了补偿，并通过主操作手重力补偿实验，验证了经过补偿后的力反馈数学模型能够改善力反馈精度，提高了遥操作骨科复位手术中的安全性。实验中没有考虑时延的问题，但是在遥操作手术中，时延的影响同样会降低力反馈精度，因此，需要进一步展开研究。

[1]徐兆红, 宋成利, 闫士举. 机器人在微创外科手术中的应用[J]. 中国组织工程研究, 2011, 15(5): 6598-6601.

[2]宋爱国. 力觉临场感遥操作机器人: 技术发展与现状[J]. 南京信息工程大学学报: 自然科学版, 2013(1): 1-9.

[3]CUI B, JIN Z. Statics analysis and structure parameter design of robot shoulder joint based on orthogonal mechanism[J]. Optics and Precision Engineering, 2011, 21(1): 15-19.

[4]VU, MINH HUNG, UHN JOO NA. A new 6-DOF haptic device for teleoperation of 6-DOF serial robots[J]. Instrumentation and Measurement, IEEE Transactions on 2011, 11(6): 3510-3523.

[5]YU L, SONG H. A new asymmetrical mass distribution method on the analysis of universal force-sensing model for 3-DOF translational parallel manipulator[J]. Industrial Robot: An International Journal, 2014, 41(1): 56-69.

[6]王宏民, 吕雄飞. 主操作手重力补偿下的时延控制[J]. 黑龙江科技大学学报, 2014(3): 272-276.

[7]王宏民, 杜志江, 闫志远, 等. 混联式主操作手重力补偿算法[J]. 机器人， 2014， 36(1): 111-116.

[8]苏宇锋, 袁文信, 刘德平, 等. 基于 BP 神经网络的电主轴热误差补偿模型[J]. 组合机床与自动化加工技术, 2013 (1): 36-38.

[9]黄剑平. 基于 BP 神经网络的 PID 控制研究[J]. 计算机仿真, 2010 (7): 167-170.

[10]王松, 刘明光, 石双双, 等. 基于卡尔曼滤波和神经网络的 PMSM 参数辨识[J]. 北京交通大学学报, 2010, 34(2): 124-127.

(编辑李德根)

Error compensation for force feedback model of robot manipulator

SONGYingying1,PIZhigang1,WANGHongmin1,NIEXiangju2

(1. School of Electrical & Control Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China;2. School of Electrical & Information Engineering, Heilongjiang Institute of Techonology, Harbin 150050, China)

This paper proposes a force feedback mathematic model based on the surgeon’s action requirements during orthopedic surgery and the characteristics of the robot in the slave side. The error of force exists between master and slave side, as is suggested by the feedback force acquired by sensors in the slave side and the input force in the master side. Reducing the force feedback error as soon as possible is made possible by using an error compensation method based on three layers BP neural network. The validity of the error compensation method is validated by developing a force feedback experiments system. The experiment suggests that error compensation leaves the force feedback error mean reduced to 0.1 N. The compensation control algorithm could improve the accuracy of force feedback model.

orthopedic surgery; manipulator; force feedback; error compensation

2016-02-02

哈尔滨市应用技术研究与开发项目(2014RFQXJ30)；黑龙江省教育厅科学技术研究项目(12541723)

宋莹莹(1980-)，女，黑龙江省哈尔滨人，高级工程师，研究方向：自动控制、电气工程，E-mail：15937228@qq.com。

10.3969/j.issn.2095-7262.2016.02.018

TN953

2095-7262(2016)02-0197-05

A