旋转不变特征描述子的点云自动配准方法

黄欢欢，程　旭，钟　凯，李中伟，史玉升，何万涛,2

(1.华中科技大学 材料成形与模具技术国家重点实验室，武汉 430074；2.黑龙江科技大学 现代制造工程中心，哈尔滨 150022)



旋转不变特征描述子的点云自动配准方法

黄欢欢1，程旭1，钟凯1，李中伟1，史玉升1，何万涛1,2

(1.华中科技大学 材料成形与模具技术国家重点实验室，武汉 430074；2.黑龙江科技大学 现代制造工程中心，哈尔滨 150022)

针对不同视角下获取的三维点云数据，提出一种基于旋转不变特征描述子的点云自动配准方法。该方法通过引入旋转不变特征描述子，可以在不依赖点云初始空间姿态前提下，计算得到待匹配点云间的初始位置关系，完成粗配准；针对配准过程中可能存在的错误匹配，提出了一种刚性变换一致性检验算法，用于实时监督多视角三维重建过程，有效避免误匹配对于重建结果的影响；精配准阶段采用改进的迭代最近点算法完成二次配准。实验结果表明：该算法具有稳定性强、重建精度高的优点，能够满足多视点云配准的要求。

机器视觉； 自动配准； 特征描述子； 一致性检测

0　引　言

面结构光三维测量法作为一种测量速度快、精度高的非接触式光学测量方法，被广泛应用于工业零件检测、产品质量控制、生物医学和历史文物保护等领域[1-3]。在测量过程中，由于被测物自身和环境的遮挡以及测量范围的限制，单次测量结果通常只能得到部分表面三维数据，因此，需要从多个视角对被测物进行测量以获得完整三维数据。其中三维点云配准，即通过寻找点云之间正确的对应关系，将从不同视点测量得到的数据转换到统一的全局坐标系，成为解决被测物三维测量数据拼合与完整重建的关键。

点云配准采用最多的方法是Besl等[4]提出的ICP(Iterative closet point)算法，其核心思想是通过迭代寻找对应点集中的最近点作为对应点，不断优化刚性变换矩阵来逼近最佳配准结果。由于该方法要求两片点云存在包含关系且初始位置相近，故，目前点云配准方法通常采用粗配准与精配准相结合的方式。粗配准采用的方法主要四种：第一种手动配准,该方法通过人工选取两片点云之间的对应点实现配准，配准的效果往往依赖操作者的经验；第二种标志点配准[5],该方法通过在被测物体上人为地粘贴标志点，再将这些标志点进行辅助配准，计算简单，但粘贴的过程较为耗时，粘贴的标志点会干扰被测形貌的特征且有些特殊场合(如珍贵文物、精密零件等)不允许粘贴标志点；第三种运动定位装置辅助配准,该方法利用转台[6]、机械臂等装置来实现辅助配准，需要预先对运动装置进行标定，测量范围受定位装置运动范围的限制，并对环境的要求较高；第四种基于自身形貌特征的配准方法,利用被测物体自身的形貌、特征来实现点云的自动配准,针对基于自身形貌特征的配准方法，已有研究单位进行相关研究并取得了一定的成果。Huber等[7]引入旋转图像特征描述方法(Spin image)对待匹配点云进行几何特征点的查找和匹配，但对点云噪声以及点云密度变化较为敏感。Rusu等[8]利用特征点与周围邻域点的法向量夹角作为特征，构建了一种快速点特征直方图(Fast point feature histograms，FPFH)用于特征点的查找和匹配，该方法计算效率较高，但要求点云具有明显的几何特征。Mian等[9]使用包围盒选取局部区域，通过计算该区域的张量特征实现配准，抗噪声能力强，但要求待匹配点云之间有较高的重叠率。戴静兰等[10]采用主方向贴合法实现点云配准，但该方法只适用于初始位置差异较小的点云数据。

目前，点云配准方法对一定情况下的点云能够取得良好的配准效果，但有些方法需要额外辅助装置，有些方法对点云的几何形貌和点云的密度、噪声程度和初始位置等有一定的要求，否则很难得到满意的配准结果，因此，对特征点的描述构建及匹配还需进一步研究。在进行点云配准时，被测量物体的形状特征不同、相同条件下获取的点云数据也有较大区别且配准过程中可能存在错误的匹配，因此，如何增强点云配准算法的适用性和稳定性，以及对错误的点云配准进行有效检测也是值得进一步研究的方向。针对上述点云配准中存在的问题，笔者提出一种基于旋转不变特征描述子的三维点云自动配准方法，该方法从粗配准入手，利用点的旋转不变特征进行特征点匹配，点的特征描述子的构建及匹配过程不依赖点云初始空间姿态，能够实现视角相差较大具有部分重叠点云数据的自动准确配准；对粗配准过程中可能出现的错误配准，设计刚性变换一致性检测算法对配准结果进行检测，排除错误的配准，进而提高算法的稳定性，结合改进的ICP算法，进行点云的精配准。

1　点云的粗配准

基于旋转不变特征描述子的点云自动配准方法首先利用旋转投影统计[11-12](Rotational projection statistics，RoPS)方法提取两片点云中特征点的RoPS特征并进行匹配，得到点云之间的初始对应关系；采用随机采样一致算法(Random sample consensus，RANSAC)对初匹配点集中存在的误匹配点进行去除；此外，为提高自动配准算法的稳定性，使用刚性变换一致性的检测算法校验得到的粗配准结果是否正确；在精配准阶段，采用一种改进的ICP算法优化点云数据间的刚性变换关系。

1.1基于RoPS的特征点匹配

RoPS特征描述子是一种具有三维空间旋转平移不变性的特征描述子。 该计算思路是利用点云数据表面关键点及其邻域的整体三维形貌关系，建立以关键点为中心且具有旋转平移不变性的局部坐标系，在构建的局部坐标系中通过对局部点云进行绕轴旋转、投影至二维平面等操作，将多视角下点云数据的空间信息转化为高维统计向量，最终构成特征描述。该特征描述子对点云密度变化、环境遮挡等干扰因素具有较强的鲁棒性。

对待配准的两幅点云数据P和Q，三维点的数目分别为M和N。由于局部特征描述子的建立依赖特征点及其周围邻域点的空间信息，相近位置点的局部特征描述差异很小，为了避免特征信息冗余，同时减少不必要的计算，因此，在进行特征提取的过程中，不需要对点集中所有的点进行局部特征的计算。文献[11]中是对网格数据求取RoPS特征，笔者则是直接对三维点云数据求解，避免对点云进行网格划分，提高了效率。文中随机选取P、Q上的若干个点构成两组特征点集，对选取的特征点求解特征点的RoPS特征描述子[11]，求解过程，如图1所示。计算得到的某一特征点的RoPS特征直方图，如图2所示，其中横坐标表示直方图区间序号，纵坐标表示归一化后的特征值。

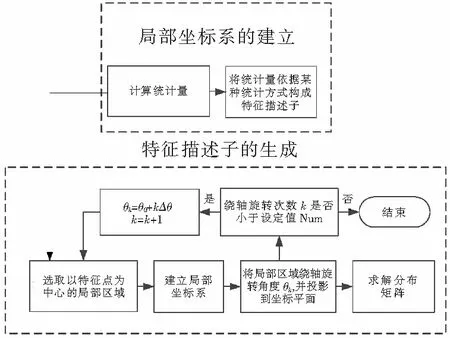
图1　RoPS特征描述子的构建

图2　点的RoPS特征直方图

Fig.2RoPS Feature histograms for one point of a point cloud

在计算得到两幅点云的一系列特征点的特征描述之后，可以对两幅点云进行特征点匹配。特征点匹配是指寻找点云特征点之间的正确对应关系。设F={f1,f2,…，fm}和F′={f1′,f2′,…，fn′}分别是点云P、Q中特征点的RoPS特征的集合，其中fi和fj′为特征点的RoPS特征描述子，m、n为P和Q中选取的特征点的个数i=1,2,…，m-1,m；j=1,2,…,n-1,n。在理想情况下，两幅点云之间互相重叠的区域具有相同的几何形貌，重叠区域内对应位置的特征点也具有相同的局部邻域，因此，两幅点云之间对应位置特征点的局部旋转不变特征描述也相同。由于该旋转不变特征的描述形式为高维向量，对应位置特征点的RoPS特征在高维空间中处于相同位置。因此，可以通过在高维特征空间中进行最近邻(Nearest neighbor)搜索来完成两幅点云间特征向量的大致匹配，即对点集P的特征点集中的任意一个特征点pi，其RoPS特征为fi，在由F′构成的特征空间中搜索满足式(1)的特征向量fj′：

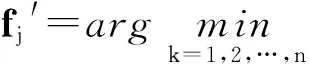
(1)

在实际过程中，测量结果可能会引入测量误差和噪声，环境遮挡也会造成点云数据的缺失，仅仅搜索相邻点云特征空间中的最近邻特征作为对应结果不能保证匹配结果的正确性。为了优化特征点的对应关系，文中引入特征空间距离比阈值以对匹配结果进行进一步的约束，通过将高维特征空间中最近邻与次近邻特征到待匹配特征之间的欧氏距离的比值作为指标，设立距离比阈值对上述匹配结果进行优化[13]。具体步骤，首先，找出与RoPS描述子fi欧氏距离最近的两个特征点描述子fj′和fj′′，然后，计算fi与fj′以及fi与fj′′两组特征向量的欧氏距离比值τ。如果比值τ小于设定的阈值ψ，则认为匹配成功，特征(fi,fj′)所对应的三维点(pi,qj′)视为一对初始匹配点；否则匹配失败。值得注意的是，在匹配的过程中，对特征fi在特征集合F′中，可能有若干个特征与其相匹配，需要对其进行进一步处理。为了降低查找匹配点的计算复杂度，提高计算的效率，文中采用ANN(Approximate nearest neighbors)来进行高维特征空间的快速最近邻点的查找。

采用上述方法提取两片点云中特征点的RoPS特征并进行特征点匹配后得到初匹配点集。RoPS特征描述子具有较强的描述性和鲁棒性，由于所选点的重复性不足，以及测量误差等因素的影响，会出现一对一或者一对多的误匹配。误匹配点的存在大大影响粗配准算法的稳定性以及刚体变换矩阵估计结果的精确性。为此，文中引入RANSAC算法[14]去除误匹配点，其基本思想是，对包含有异常值的输入数据构建数学模型，根据一定的相关评判标准，将数据分成内点和外点两种，利用内点比较准确的优点计算出当前最佳目标模型参数，经过一定次数的抽样迭代直至条件收敛，计算出最终的最佳目标模型参数。采用RANSAC算法进行误匹配点排除后，得到优化后的初匹配点集。

对熊猫模型从不同角度进行测量获得的共9幅点云数据，如图3a所示。任意选取其中两片相邻数据如图3b所示进行上述特征点匹配，然后进行误匹配点去除操作，结果如图3c所示。实验结果表明采用RANSAC算法可有效排除误匹配点，提高了RoPS特征对应点的匹配精度。

a　熊猫模型点云数据

b　未采用RANSAC算法

c　采用RANSAC算法

1.2刚性变换一致性检测

RoPS特征的匹配不依赖于点云初始空间的姿态关系，但若两片点云的重合区域较小，使特征匹配时得到的对应点数目较少或RoPS特征之间的差异较小时，采用RANSAC算法可能得到错误的变换矩阵，以致最终得到错误的配准结果。一般配准结果校验方法是计算对应点集之间的距离进行判定，但此方法对数据量较大的配准点云进行检验时，计算复杂程度高[15]。文中提出一种粗配准刚性变换一致性检测方法，即根据两片点云数据的重叠区域的整体形状与局部形状具有刚性变换不变性的特点，分别采用RANSAC算法估计点云整体的刚性变换关系，以及利用多对局部特征对应关系来求解点云局部区域的刚性变换关系，通过对上述两种方法估计得到的刚性变换关系进行互相验证，最终作为刚性变换估计是否正确的依据。此方法采用相互验证的方法具有较强的可靠性且计算的效率高，能够避免粗配准的错误配准结果对精配准过程的影响，具体步骤：

(1)对RANSAC算法优化后的初匹配点集中的匹配点(pnl,qnl) 计算匹配点之间的旋转平移矩阵(Rnl,Tnl)，其中nl=1,2,…，S-1,S;S为初匹配点集中匹配点的数目；将求解得到的旋转矩阵Rnl转换为欧拉角表示，即Rnl→(anl,βnl,γnl)。将采用RANSAC算法计算得到的旋转矩阵Rnr转化为欧拉角表示，即Rnr→(anr,βnr,γnr)；

(2)根据式(2)计算欧拉角之间的角度差值da:

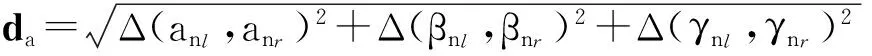
(2)

其中,Δ(η1,η2)2=(η1-η2)2,η1、η2为欧拉角。

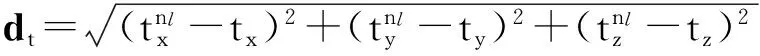
(3)

(4)若da和dt均小于给定的阈值σa和σt，则认为是两种方法求解出的旋转平移矩阵是相近的，统计满足该条件的点的数目s。

(5)计算s和S的一致性比值λ=s/S，若λ大于给定的阈值ω，则说明利用RANSAC求解得到的旋转矩阵和利用局部旋转不变坐标系计算得到的旋转矩阵是一致的，即配准成功；否则说明配准失败，分析此种情况出现的原因是这两幅点云之间的测量视角偏差过大，点云间的重叠区域过小，使匹配得到的对应点较少，最终导致配准错误，可调整被测物体的位置并再次进行测量。

采用前述RoPS方法进行特征点的查找和匹配，并使用一致性检测方法对配准结果进行检验后，得到点云间的初始刚性变换矩阵，实现粗配准。

1.3改进ICP算法的精配准

利用上述算法获得初始配准参数后，完成粗配准，满足了ICP算法对点云初始位置和两片点云存在包含关系的要求，文中采用改进的ICP算法对配准结果进行进一步优化，具体步骤：

(1)随机在源点云中选取若干点作为待匹配点，取代使用所有点作为匹配候选点，提高了计算效率。

(2)采用投影法在目标点云中查找对应点，即沿着目标点云的视点，将源点云上的点向目标点云表面投影，与投影线相交的点视为对应点，此方法查找对应点的时间复杂度大大提高了对应点查找的搜索效率。

(3)采用点到面的最小距离取代点到点的距离为目标函数，降低了迭代的次数且迭代过程中不易陷入局部极值。

2　实验数据与应用效果分析

为验证所提方法可行性，文中从三个方面进行了实验设计：(1)一致性检测算法的有效性；(2)针对不同形貌特征的被测物体位置偏差较大的两幅点云能否准确配准；(3)对整体模型进行测量配准时出现的错误配准能否进行有效检测，以及对不同模型整体配准后进行精度分析。文中采用实验室组装的基于面结构光三维测量设备获取点云数据进行实验验证。所用测量设备主要由两个工业相机和一个数字光栅投影仪组成，单次测量范围是500 mm×400 mm，景深为300 mm，单次测量误差为±0.05 mm。

2.1一致性检测实验

文中提出的刚性变换一致性检测方法采用全局约束和局部约束方法分别计算点云的粗配准变换矩阵，并进行相互验证所求矩阵的正确性。其中，两种约束求解得到的刚性变换矩阵均是对点云位置的大致估计，并不是精确求解，故衡量两个矩阵是否一致时对阈值的选取没有严格的限定。文中通过实验得到角度差值阈值σa选取π/6，距离差值阈值σt选取15Dden，Dden为点云密度，即旋转矩阵的角度相差小于30°，平移矩阵距离的差值小于15倍点云密度时，可判断两个旋转平移矩阵是一致的。在计算一致性比值λ时，求解得到的结果呈现出两极分化的趋势，若阈值取得太大，则会引入大量错误的刚性变换矩阵，影响一致性检测结果的准确性；若阈值取得过小，则计算得到的变换矩阵不能满足要求，难以达到一致性检测的目的。经实验验证一致性阈值在取为0.7时，可取得良好的检验结果。下面对刚性变换一致性检测方法的有效性进行实验验证。

文中采用的实验数据是图3a的9幅功夫熊猫的点云数据，按测量顺序依次对点云数据进行编号1～9。利用1.1中所述方法对两两相邻的点云数据(如第3，4幅数据)，以及两两不相邻的点云数据(如第1，6幅数据)进行自动配准。根据上述配准结果，一方面，通过人工判断上述配准过程是否实现了两幅点云数据的大致拼合，从而确定两幅数据之间的自动配准结果是否成功，并以此作为一致性检验结果的参照；另一方面，采用一致性检测方法对配准结果进行一致性检测，与人工判断结果进行对照，验证文中提出的刚性变换一致性算法是否有效。具体实验数据如表1所示，其中点云序号(i，j)表示对第i，j幅数据的配准结果进行一致性检测。

由表1可知，实验得到的一致性检测结果与人工判断结果一致，验证了文中提出的刚性变换一致性算法的正确性和有效性。其中，第1幅和第9幅点云数据存在较多的重叠区域，对两者进行匹配可以得到较多的匹配特征点，进而得到正确配准结果，如图4a所示。两幅数据一致性检测比值为0.960，远大于设定的阈值，有效检测得到两幅点云配准成功；而第1幅和第6幅点云数据分别来自功夫熊猫的正面与反面，两者几乎没有重叠区域，直接对其进行自动配准无法得到正确的特征点对应关系，不能实现正确配准，如图4b所示。两幅数据的一致性检测比值为0.090，远小于设定阈值，有效检测得到点云配准失败。通过上述实验充分验证了文中提出的刚性变换一致性检测方法的有效性，可用于点云的自动配准结果检验。

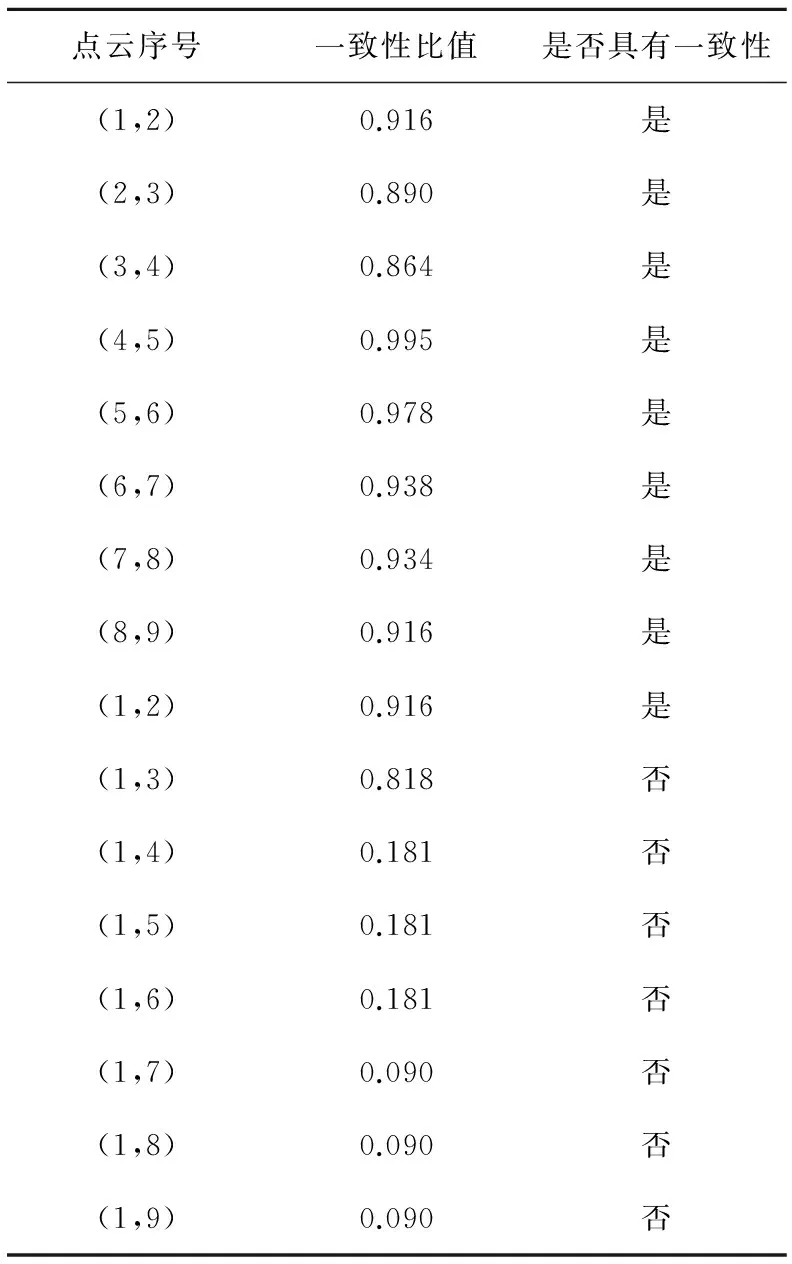
表1　一致性检测

a　点云1和9配准结果

b　点云1和6的配准结果

2.2不同被测物体和整体模型的配准实验

采用上述设备对图5a所示的不同曲面的实物(鼠首和工件)进行多角度测量，且保证两两相邻的测量数据有部分重叠。如图5b所示，从测得的点云数据中任选两片相邻点云数据进行配准实验：(1)采用ICP算法对视差较大的初始点云数据进行配准，结果如图5c所示。由图5c可见，由于初始点云之间的空间相对位置偏差较大，直接采用ICP算法无法得到正确的配准结果。(2)采用文中提出配准方法对初始点云进行配准，结果如图5d所示。从图5d可以看出，两片点云数据配准成功，说明文中算法是有效可行的。实验结果对比表明：文中提出的算法较好地解决了ICP算法对点云初始位置的要求，可以实现位置偏差较大具有部分区域重叠的不同曲面点云数据的自动配准。

a　实物

b　未拼接点云

c　ICP配准

d　RoPS粗配准,ICP精配准

为了更好验证文中所提算法对模型进行测量配准时的有效性，对如图6a所示的彩陶马模型(300 mm×110 mm×300 mm)进行11次有重叠测量，在测量的过程中，利用提出的算法对测量得到的点云数据进行配准，在对第5幅测量数据进行配准时，采用文中提出的刚性变换一致性算法计算得到的一致性比值小于阈值，即检测出配准错误，结果如图6b所示。针对配准错误的数据，调整测量视角后再次进行测量，最终得到正确的整体配准结果，如图6c所示。

a　实物　　　b　整体点云数据　c　测量过程中的错误配准

为了进一步验证文中算法的配准精度，使用算法分别对上述四种不同曲面模型进行整体配准，计算配准前后的配准误差。文中采用均方根误差RMSE (Root mean square error) 衡量点云配准的精度。不同模型点云配准的精度变化，如图7所示。其中横坐标表示模型点云数据所处的不同阶段：初始数据、粗配准和精配准，纵坐标表示点云数据的均方根误差。

图7　不同曲面模型配准精度变化

由图7可见，经过粗配准后模型点云数据的均方根误差均显著降低，可知文中采用的粗配准算法完成了不同模型点云空间位置的大致变换，满足了ICP算法中对点云初始位置的要求。在精配准阶段，采用改进的ICP算法对点云配准结果进行优化，进一步降低了均方根误差提高了点云的配准精度，点云模型配准的最终误差均分布在0.23～0.55 mm之间，可知文中算法能够满足点云配准的实际精度要求。

3　结束语

基于物体自身形貌特征的点云配准方法，因其具有自动化程度高、适用性广等优点，已成为点云配准研究的重点，针对现有算法存在的问题，提出了一种基于旋转不变特征描述子的三维点云自动配准方法。该方法利用点的RoPS特征进行特征点匹配，配准的过程中采用RANSAC算法对误匹配的特征点进行剔除，并提出了刚性变换一致性检测算法来检验配准结果的正确性，最后采用改进的ICP算法对粗配准结果进行优化，实现点云的自动精确配准。通过一致性检测实验和对不同物体的配准实验对所提方法的有效性进行了详细验证，结果表明，文中所提出方法具有较强的稳定性。

[1]李中伟，史玉升，钟凯，等.结构光测量技术中的投影仪标定算法[J].光学学报，2009，29(11):3061-3065.

[2]ZHONG K，LI Z W，ZHOU X H，et al.Hybrid parallel computing architecture for multiview phase-shifting[J].Optical Engineering，2014，53(11)：112214.

[3]伍梦琦，李中伟，钟凯，等.基于几何特征和图像特征的点云自适应拼接方法[J].光学学报，2015，35(2)：215-220.

[4]BESl P J，MCKAY N D.A method for registration of 3-D shapes[C]//Pattern Analysis and Machine Intelligence，IEEE Transactions on Pattern Analysis and Machine Intelligence，1992，14(2)：239-256.

[5]宋丽梅,陈昌曼,陈卓,等.环状编码标记点的检测与识别[J].光学精密工程，2013，21(12)：3239-3247.

[6]周朗明，郑顺义，黄荣永.旋转平台点云数据的配准方法[J].测绘学报，2013，42(1)：73-79.

[7]HUBER D F，HEBERT M.Fully automatic registration of multiple 3D data sets [J].Image and Vision Computing，2003，21(7)：637-650.

[8]RUSU R B，BLODOW N，BEETZ M.Fast point feature histograms (FPFH) for 3D registration[C]//Robotics and Automation IEEE International Conference，IEEE，2009：3212-3217.

[9]MIAN A S，BENNAMOUN M，OWENS R A.A novel representation and feature matching algorithm for automatic pairwise registration of range image [J].International Journal of Computer Vision，2006，66(11)：19 -40.

[10]戴静兰，陈志杨，叶修梓.ICP算法在点云配准中的应用[J].中国图象图形学报，2007，12(3)：517-522.

[11]GUO Y L，FERDOUS S，BENNAMOUN M，et al.Rotational projection statistics for 3D local surface description and object recognition.International Journal of Computer Vision，2013，105 (1)：63-86.

[12]GUO Y L，FERDOUS S，BENNAMOUN M，et al.An accurate and robust range image registration algorithm for 3D object modeling[J].Multimedia IEEE Transactions on，2014，16(5)：1377-1390.

[13]LOWE D.Distinctive image features from scale-invariant keypoints[J].IJCV，2004，60(2)：91-110.

[14]雷玉珍，李中伟，钟凯，等.基于随机抽样一致算法的误匹配标志点校正方法[J].光学学报,2013,33(3)：205-212.

[15]YANG J Q，CAO Z G，ZHANG Q.A fast and robust local descriptor for 3D point cloud registration[J].Information Sciences，2016，34(6)：163-179.

(编辑李德根)

Point cloud registration method based on rotation invariant feature descriptor

HUANG Huanhuan1，CHENG Xu1，ZHONG Kai1，LI Zhongwei1，SHI Yusheng1，HE Wantao1,2

(1.State Key Laboratory of Material Processing &Die &Mould Technology,Huazhong University of Science &Technology,Wuhan 430074,China; 2.Manufacture Engineering Center,Heilongjiang University of Science &Technology,Harbin 150022,China)

This paper proposes an automatic point clouds registration algorithm based on rotation-invariant local feature descriptor for three-dimensional point cloud data obtained under different views.This algorithm works first by introducing a rotation-invariant local feature descriptor to determine point correspondences;then by estimating initial transformation without any prior available information of initial position and providing a novel rigid transformation consistency verification method designed for possible registration errors occurring in coarse registration process to supervise multi-view point clouds’ reconstruction in real-time,thus effectively avoiding mismatch impact;and ultimately by completing the fine registration using a variant of iterative closest point algorithm.The experiments show that our method capable of more accurate and robust automatic point clouds registration is adequate for multi-view registration.

machine vision;automatic registration;feature descriptor;transformation consistency verification

2016-05-05

国家科技重大专项(2013ZX02104004-003_IC)；国家自然科学基金项目(51505134)；湖北省重大科技创新计划项目(2013AEA003)；科技支疆专项计划资助项目(2014AB032)

黄欢欢(1989-)，女，安徽省淮北人，硕士，研究方向：三维测量和点云处理，E-mail：zwli@hust.edu.cn。

10.3969/j.issn.2095-7262.2016.03.017

TP301.6

2095-7262(2016)03-0316-07

A