蜂窝钢板剪力墙地震响应分析

袁朝庆，王义荧,刘　彦

(1.东北石油大学 土木建筑工程学院，黑龙江 大庆 163318；2.黑龙江省防灾减灾及防护工程重点实验室，黑龙江 大庆 163318)



蜂窝钢板剪力墙地震响应分析

袁朝庆1,2，王义荧1,2,刘彦1,2

(1.东北石油大学 土木建筑工程学院，黑龙江 大庆 163318；2.黑龙江省防灾减灾及防护工程重点实验室，黑龙江 大庆 163318)

为了提高结构的抗震能力，应用有限元软件ADINA，建立一个十二层钢框架模型和两个不同高厚比下的蜂窝钢板剪力墙模型，研究其在8度多遇地震和罕遇地震作用下的加速度时程曲线、最大顶点位移时程曲线以及楼层最大侧移和最大层间位移角响应。选取EL-Centro、Taft和人工三种波比较分析，结果表明：十二层钢框架和不同高厚比下的蜂窝钢板剪力墙，在罕遇地震波作用下的响应比多遇地震波作用下的响应强烈；在地震波作用下三种结构均未发生破坏，蜂窝钢板剪力墙的最大层间位移角小于钢框架结构，具有更好的抗震性能。

蜂窝钢板剪力墙； 地震响应； 时程分析

随着钢结构的广泛应用，钢板剪力墙结构在抗震中表现出良好的抗震性能，成为一种新型抗侧力体系[1]。目前，我国学者正致力于研究新型的建筑结构形式，如带缝钢板剪力墙和开洞钢板剪力墙[2-3]，通过降低钢板的刚度来增加其延性，提高结构的抗震能力。笔者旨在研究蜂窝钢板剪力墙(即在钢板上开圆孔或六边形孔)的抗震性能。蜂窝钢板剪力墙与普通钢板剪力墙相比，除延性好、自重小以及施工方便等外，还方便调整钢板剪力墙的外围尺寸和开孔形式，用钢量有所降低。因此，文中对蜂窝钢板剪力墙地震响应作了分析研究。

1　有限元方法与验证

1.1有限元方法

选择文献[4]中的实验模型，采用有限元分析软件ADINA模拟实验中的钢板剪力墙结构在低周往复荷载作用下的抗震性能。钢填充板、钢框架梁和钢框架柱均采用壳单元模拟。有限元模型各部分的材料属性和实常数根据试件的材性实验结果以及试件各部分板件的实际厚度确定,材料模型选用双线性随动强化本构模型，运用 Full Newton-Raphson迭代法求解非线性方程组，材料采用Mises屈服准则。研究有限元模型在循环荷载作用下的抗震性能，其加载采用实验加载制度。

1.2实验与理论数据对比

实验和有限元模拟得到的滞回曲线[5]，见图1。由图1可见，有限元模拟钢板剪力墙结构与实验所得滞回曲线趋势相似，滞回曲线饱满，说明结构具有良好的滞回性能。将得到的有限元数据与文献[4]实验数据和文献[6]ABAQUS模拟的数据进行对比，对比结果如表1所示。

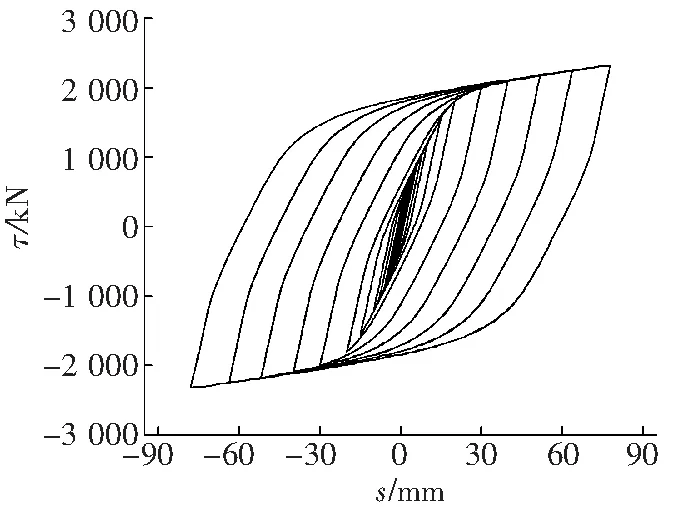
图1　ADINA滞回曲线

数值抗侧刚度/kN·mm-1极限承载力/kN文献[4]实验值1151770文献[6]模拟值1421975有限元模拟值1462130

从表1可以看出，ADINA有限元模拟结果与实验结果相比，抗侧刚度偏高26.08%，承载力偏高20.33%。这可能是由于有限元模型上施加的约束强于实验中的实际约束；有限元模型定义的材料为理想材料，没有考虑初始缺陷和材料缺陷等。有限元模拟值与文献[6]中模拟值的抗侧刚度和极限承载力误差相差不大，分别为2.8%和4.2%。说明采用ADINA有限元软件对钢板剪力结构进行抗震性能模拟的方法可行。

2　蜂窝钢板剪力墙地震响应分析

2.1有限元计算模型

采用壳单元建立十二层蜂窝钢板剪力墙结构和钢框架结构有限元模型，如图2a和2b 所示。填充钢板与钢框架完全固结，模型底端固定，上端只约束平面外位移，左右两边自由。钢填充板的屈服强度为235 MPa,钢框架的屈服强度为345 MPa,其弹性模量均为206 GPa，泊松比均为0.3，钢框架梁、柱分别为型钢Q345H 250 mm×125 mm×6 mm×9 mm和型钢Q345H 200 mm×200 mm×8 mm×12 mm[7]。内填钢板长2.7 m，高2.6 m。开孔形式为直径200 mm的圆孔，开孔率为7.6%，圆孔布置方式见图2c。

对比分析十二层蜂窝钢板剪力墙结构和钢框架结构在8度多遇和罕遇地震作用下的受力性能，研究地震波对结构最大加速度、最大位移和层间位移角的影响。蜂窝钢板剪力墙结构的高厚比分别取200和400。以符号A代表高厚比为400的蜂窝钢板剪力墙，符号B代表高厚比为200的蜂窝钢板剪力墙，Frame代表钢框架结构。

a　蜂窝钢板剪力墙　b　钢框架　　　　c　圆孔布置方式

2.2地震波的选取

按照GB 50011—2010《建筑抗震设计规范》[8]的规定，以及地震波的相关数据记录，选取EL-Centro波、人工波和Taft波作为输入地震波，II类场地详见图3，三种地震波时间间隔为0.02 s，持时10 s，加速度a峰值依次为3.417、1.960和1.527 m/s2。规范规定，8度多遇地震下的地震加速度时程最大值为70(110) cm/s2，罕遇地震下的地震加速度时程最大值为400(510) cm/s2，括号内数值分别用于设计基本地震加速度为0.15g和0.30g的地区。在进行抗震性能分析时，需要对文中选取的三种地震波幅值按地震波输入要求进行调整。

a　EL-Centro波

b　Taft波

c　人工波

2.3多遇地震下蜂窝钢板剪力墙地震响应分析

2.3.1加速度时程分析

三种结构在三种多遇地震波作用下的顶点最大加速度时程曲线,如图4所示。

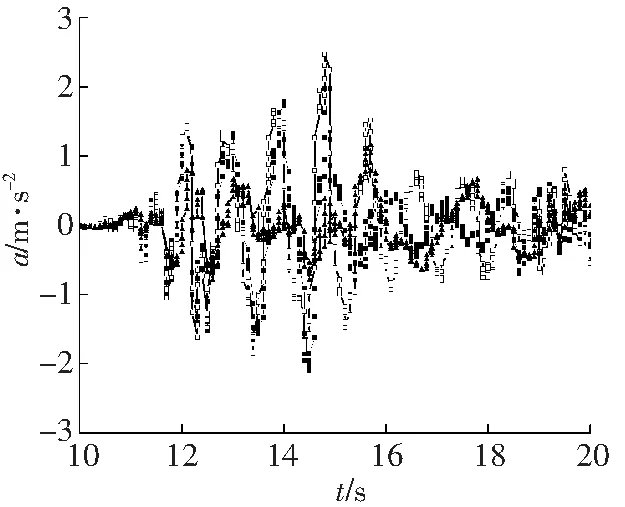
a　EL-Centro波

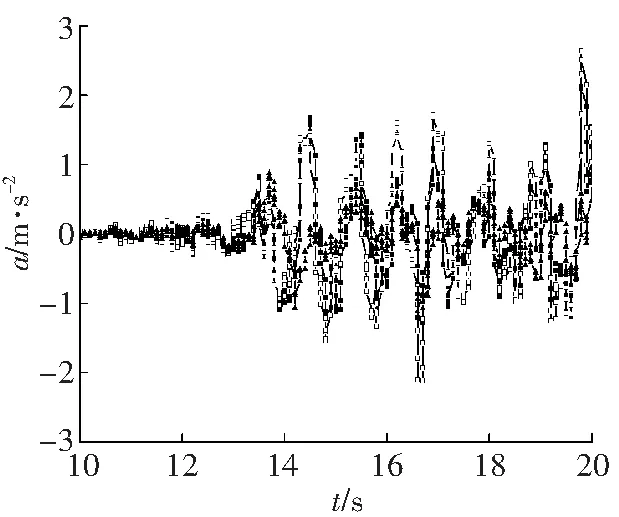
b　Taft波

图4　不同地震波作用下的顶点绝对最大加速度值

Fig.4Acceleration time history curves under different seismic waves

从图4可以看出，三种结构在同一种地震波作用下的加速度时程曲线变化趋势和所输入的地震波变化趋势基本保持一致；A、B和Frame的顶点最大加速度放大系数在EL-Centro波作用下分别为2.9、3.5和1.6，在Taft波作用下分别为3.0、3.7和1.2；在人工波作用下分别为1.3、1.36和1.03。A和B结构的放大系数均比Frame结构放大系数大，A与B相比，在EL-Centro波、Taft波以及人工波作用下，A的放大系数依次是B的0.83倍、0.81倍和0.96倍，这主要是由于镶嵌了蜂窝钢板使框架结构的质量增大，从而使地震加速度响应增大，而A的内嵌钢板较B薄，质量较小，所以地震加速度响应较小。

2.3.2位移时程分析

结构在三种多遇地震波作用下顶点最大位移sdmax时程曲线，如图5所示。

a　EL-Centro波

b　Taft波

图5　不同地震波作用下的顶点最大位移时程曲线

Fig.5Maximum vertex displacement curves under different seismic waves

由图5可见，蜂窝钢板剪力墙在同一种地震波作用下的顶点最大位移时程曲线变化趋势基本保持一致，钢框架位移峰值的延时现象较为明显，其最大位移出现的时刻明显晚于蜂窝钢板剪力墙。在EL-Centro波作用下，A、B的顶点位移峰值分别约为Frame的0.61倍和0.58倍;在Taft波作用下，分别约为0.81倍和0.69倍;在人工波作用下，分别约为0.94倍和0.81倍。在EL-Centro波、Taft波以及人工波作用下，A的顶点位移峰值依次是B的1.05倍、1.17倍和1.16倍。A和B的最大顶点位移均小于Frame，且A的最大顶点位移略大于B，这主要是由于蜂窝钢板的存在使框架结构的抗侧刚度提高，而B的蜂窝钢板较A厚，抗侧刚度更高，能够降低结构最大顶点位移。

2.3.3层间位移角

结构在三种多遇地震波作用下的楼层最大侧向位移slmax和楼层最大侧向位移角γ分别如图6和图7所示。

a　EL-Centro波

b　Taft波

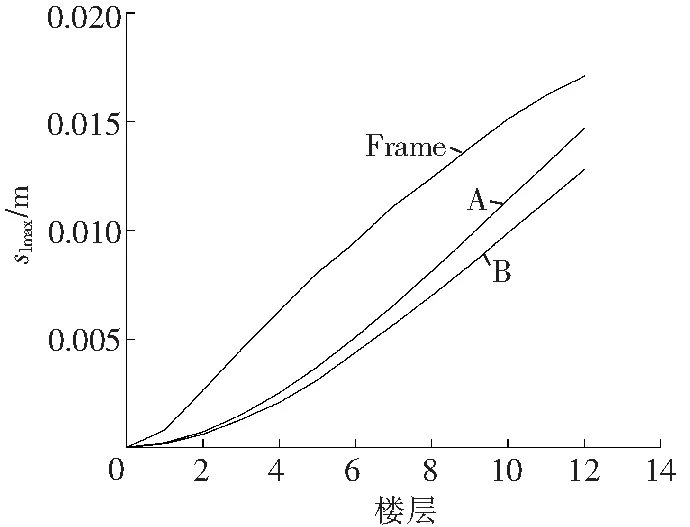
c　人工波

Fig.6Maximum lateral displacement under different seismic waves

从图6可以看出，蜂窝钢板剪力墙最大侧向位移比钢框架减小很多，在EL-Centro波作用下，A、B的最大侧向位移分别约为Frame的0.61倍和0.58倍；在Taft波作用下，分别约为0.81倍和0.69倍；在人工波作用下，分别约为0.94倍和0.81倍。在EL-Centro波、Taft波以及人工波作用下，A的最大侧向位移依次是B的1.05倍、1.17倍和1.16倍。

a　EL-Centro波

b　Taft波

c　人工波

Fig.7Maximum story drift under different seismic waves

由图7可以看出，Frame的最大层间位移角出现在中下层，A和B的层间位移角自底层到顶层越来越大，增幅逐渐减小，最大值均出现在顶层。在EL-Centro波、Taft波和人工波作用下，Frame的最大层间位移角分别为1/283、1/629和1/1 209，分别出现在第四层、第五层和第四层，A的最大层间位移角分别为1/565、1/719和1/1723，B的最大层间位移角分别为1/599、1/862和1/1 946，三种结构的楼层最大侧向位移角均满足抗震规范[8]弹性层间位移角限值1/250的规定。蜂窝钢板剪力墙结构的变形主要为剪切和弯曲变形，而蜂窝钢板使钢框架结构的侧向刚度得到大幅度提高，结构的侧向位移和层间位移角显著减小。在EL-Centro波、Taft波以及人工波作用下，A的层间位移角依次是B的1.06倍、1.20倍和1.13倍，这主要是因为B的抗侧刚度大于A，故其侧向位移和层间位移角较A小。

2.4罕遇地震下蜂窝钢板剪力墙地震响应分析

2.4.1加速度时程分析

三种结构在三种罕遇地震波作用下的顶点最大加速度时程曲线，如图8所示。

a　EL-Centro波

b　Taft波

图8　不同波作用下顶点最大加速度时程曲线

Fig.8Acceleration time history curves under different seismic waves

由图8可以看出，A、B和Frame在罕遇地震作用下的顶点最大加速度时程曲线与在多遇地震下的相应时程曲线变化规律类似，但是由于输入的地震波加速度峰值增大，加速度响应较多遇地震作用下更强烈。A、B和Frame的顶点最大加速度放大系数在EL-Centro波作用下分别为2.8、3.1和1.6；在Taft波作用下分别为2.9、3.55和1.5；在人工波作用下分别为1.35、1.47和1.03。A与B相比，在EL-Centro波、Taft波以及人工波作用下，A的放大系数依次是B的0.90倍、0.82倍和0.92倍。

2.4.2位移时程分析

结构在三种罕遇地震波作用下的顶点最大位移smax时程曲线,如图9所示。

a　EL-Centro波

b　Taft波

图9　不同波作用顶点最大位移时程曲线

Fig.9Maximum vertex displacement curves under different seismic waves

由图9可见，A、B和Frame在罕遇地震作用下的顶点最大位移时程曲线与在多遇地震下的相应时程曲线变化规律类似，但是由于输入的地震波位移峰值增大，位移响应较多遇地震作用下更强烈。在EL-Centro波作用下，A、B的顶点位移峰值分别约为Frame的0.59倍和0.51倍；在Taft波作用下，分别约为0.83倍和0.71倍；在人工波作用下，分别约为0.87倍和0.74倍。在EL-Centro波、Taft波以及人工波作用下，A的顶点位移峰值依次是B的1.16倍、1.17倍和1.18倍。

2.4.3层间位移角

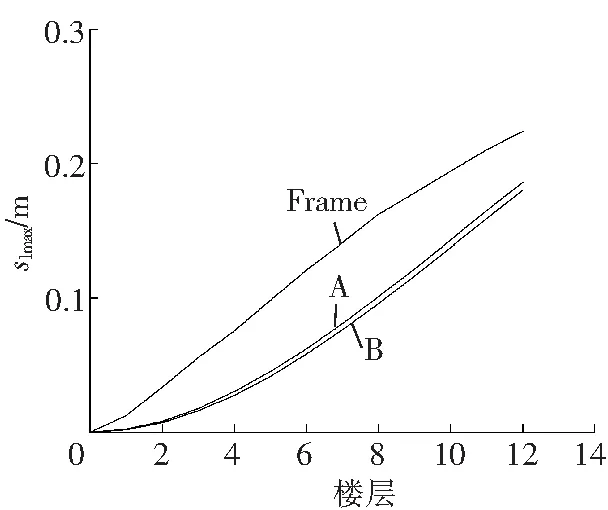
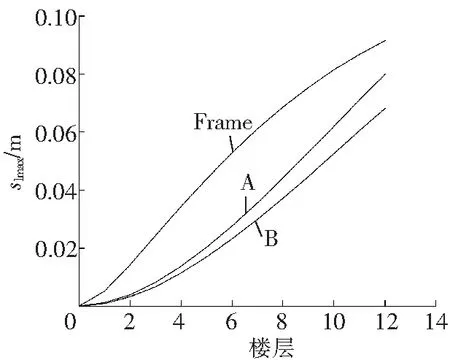
结构在三种多遇地震波作用下的楼层最大侧向位移和楼层最大侧向位移角分别如图10和图11所示。

a　EL-Centro波

b　Taft波

c　人工波

Fig.10Maximum lateral displacement under different seismic waves

由图10可以看出，A、B和Frame在罕遇地震作用下的最大层间位移和最大层间侧移角，与在多遇地震下的相应的变化规律类似，但是由于输入的地震波位移峰值增大，最大层间位移和最大层间侧移角响应较多遇地震作用下更强烈。在EL-Centro波作用下，A、B的最大侧向位移分别约为Frame的0.59倍和0.51倍，在Taft波作用下，分别约为0.83倍和0.71倍，在人工波作用下，分别约为0.87倍和0.74倍。在EL-Centro波、Taft波以及人工波作用下，A的最大层间位移依次是B的1.16倍、1.17倍和1.18倍。

a　EL-Centro波

b　Taft波

c　人工波

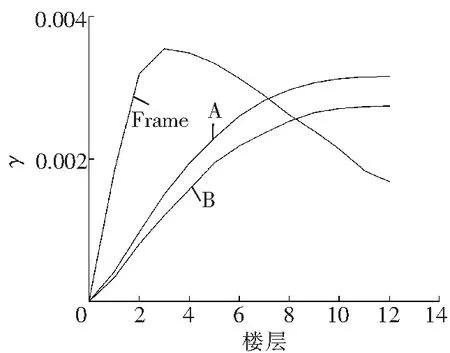
Fig.11Maximum story drift under different seismic waves

由图11可以看出，在EL-Centro波、Taft波和人工波作用下，Frame的最大层间位移角分别为1/75、1/106和1/282，分别出现在第五层、第六层和第三层，A的最大层间位移角分别为1/107、1/133和1/316，B的最大层间位移角分别为1/127、1/136和1/365。三种结构的楼层最大侧向位移角均满足抗震规范[8]弹塑性层间位移角限值1/50的规定。在EL-Centro波、Taft波以及人工波作用下，A的层间位移角依次是B的1.19倍、1.02倍和1.16倍。

3　结　论

对十二层钢框架和不同高厚比下的蜂窝钢板剪力墙，进行8度多遇地震和罕遇地震作用下的抗震性能分析，得出以下结论：

(1)同一种结构在同等烈度罕遇地震作用下的地震响应曲线的变化趋势，类似于相应多遇地震作用下的地震响应曲线，但在罕遇地震作用下的地震响应均大于在多遇地震作用下的地震响应。

(2)在同一种地震波作用下，蜂窝钢板剪力墙中的最大加速度响应大于钢框架的最大加速度响应，而最大顶点位移、最大楼层位移和最大层间位移角均小于钢框架。

(3)在同一种地震波作用下，蜂窝钢板剪力墙结构的高厚比越大，最大加速度响应越小，而最大顶点位移、最大楼层位移和最大层间位移角越大，在实际工程应用中，应根据实际情况选择合理的高厚比以降低地震对结构的损坏程度。

(4)同一种结构在不同的地震波作用下的地震响应不同，说明震害与地震波的波形有关。

(5)三种结构在罕遇地震作用下的最大层间位移角均未超过结构弹塑性层间位移角1/50的限值，说明结构均未发生破坏，但是蜂窝钢板剪力墙的最大层间位移角小于钢框架，说明蜂窝钢板剪力墙的抗震性能更好。

致谢：

该研究得到了东北石油大学研究生创新科研项目(YJSCX2015-035NEPU)的资助。

[1]聂建国，朱力，樊健生，等．钢板剪力墙抗震性能实验研究[J]．建筑结构学报，2013，34(1)：61-69．

[2]袁朝庆，刘彦，王义荧．钢框架-带缝钢板剪力墙结构抗震性能研究[J]．工程抗震与加固改造，2016，38(2)：25-31．

[3]王先铁，贾贵强，周超，等．方钢管混凝土框架-中间开洞薄钢板剪力墙抗侧承载力研究[J]．建筑结构学报，2015，36(S1)：67-73．

[4]VIAN D,BRUNEAU M,TSAI K C，et al.Special perforated steel plate shear walls with reduced beam section anchor beams.I:Experimental investigation[J].Struct Eng，2009，135(3)：211-220.

[5]姚谦峰，苏三庆.地震工程[M].西安：陕西科学技术出版社，2001.

[6]VIAN D,BRUNEAU M,TSAI K C,et al.Special perforated steel plate shear walls with reduced beam section anchor beams.II:Analysis and Design Recommendations[J].Struct Eng,2009，135(3)：221-230.

[7]袁朝庆，贺有丰，徐松芝.钢框架-带缝钢板剪力墙结构受力性能分析[J].地震工程与工程振动，2008，28(2)：96-101.

[8]GB 50011—2010.建筑抗震设计规范[S].北京:中国建筑工业出版社,2010.

(编辑徐岩)

Investigation to seismic performance of honeycomb shaped steel plate shear wall

YUAN Zhaoqing1,2，WANG Yiying1,2,LIU Yan1,2

(1.School of Civil &Architecture Engineering,Northeast Petroleum University,Daqing 163318,China; 2.Heilongjiang Key Laboratory of Disaster Prevention,Mitigation &Protection Engineering,Daqing 163318,China)

This paper seeks to meet the safety and economic needs and improve the seismic capacity of the structures.The research does this by using the finite element software ADINA to establish a twelve-storey steel frame model and two honeycomb steel plate shear wall models with different ratios of height to thickness;thereby studying the acceleration time history curve,the maximum vertex displacement curve,maximum lateral displacement and the maximum story drift of above models under the 8 degree frequent earthquake and rare case;and providing a comparative analysis under three earthquake waves,namely,EL-centro,Taft and artificial wave.The analysis shows that the responses are stronger for twelve-storey steel frame and two honeycomb steel plate shear wall with different ratios of height to thickness under the rare earthquake than for under frequent earthquake;and the better seismic performance is validated by the absence of destruction in these three structures exposed to earthquakes,leaving the maximum story drift of honeycomb steel plate shear wall smaller than that of steel frame structure.

honeycomb shaped steel plate shear wall； seismic response； time history analysis

2016-04-09

袁朝庆(1970-)，男，黑龙江省依安人，教授，博士，研究方向：工程结构抗震，E-mail：yvq@sina.com。

10.3969/j.issn.2095-7262.2016.03.009

TU398

2095-7262(2016)03-0277-07

A