线性矩阵不等式的H∞跟踪控制器设计方法
方 辉
(渤海大学 工学院, 辽宁 锦州 121013)
线性矩阵不等式的H∞跟踪控制器设计方法
方辉
(渤海大学 工学院, 辽宁 锦州 121013)
为提高线性连续时间系统的跟踪性能,提出基于线性矩阵不等式(LMI)技术的H∞跟踪控制器设计方法。利用LMI技术和Lyapunov函数方法,以H∞跟踪控制参数为性能指标,给出基于观测器的跟踪控制器存在条件。结果表明:闭环系统的状态曲线可实现对参考信号的跟踪,证明定理所给出的跟踪控制器及观测器求解方法的有效性。
H∞跟踪控制器; 线性矩阵不等式; Lyapunov函数
0 引 言
系统的稳定性能和跟踪性能是系统控制的两个典型问题,然而,相对系统的稳定性分析,跟踪控制器的设计更加困难。跟踪控制是指通过设计跟踪控制器使系统的状态变量能够跟踪某一参考信号的状态变量。文献[1]将反馈线性化技术引入到跟踪控制器的系统化设计过程中。通过这种方法设计的控制器并不能确保系统的有效性[2]。文献[3] 研究了非线性系统进的H∞跟踪控制。文献[4]处理存在外部干扰的H∞输出反馈控制线性矩阵不等式条件。针对任意有界参考信号输入,采取基于观测器的跟踪控制器设计方法,这种方法优越性在减小跟踪误差方面有所体现[5]。此外,在控制系统稳定性分析中,主要考虑的理论基础是Lyapunov稳定性理论,随着求解凸优化问题内点法的提出,LMI方法在控制理论领域中被广泛采用。诸多控制系统稳定性分析问题可通过求解线性矩阵不等式系统的可行性问题解决。随着Matlab软件推出求解矩阵不等式问题的LMI工具箱,使得线性矩阵不等式的求解过程大大简化,进一步促进了线性矩阵不等式方法在系统的稳定性能和跟踪性能相关领域的应用。鉴于上述分析,笔者针对线性连续时间系统,通过线性矩阵不等式(LMI)技术,利用Lyapunov函数方法,设计基于观测器的H∞跟踪控制器存在条件。
1 问题描述
考虑如下的连续系统状态方程,将针对该模型设计基于观测器的跟踪控制器。
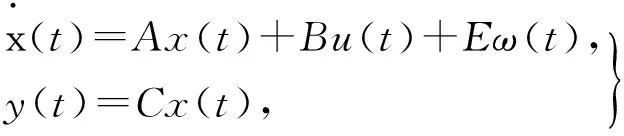
(1)
式中:x(t)——系统的状态变量;
u(t)——系统输出的控制变量;
ω(t)——系统的扰动变量;
y(t)——系统的输出变量;
A、B、C、E——系统的系数矩阵。
为实现系统的跟踪控制,考虑参考模型如下[5]:
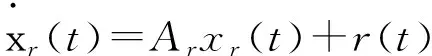
(2)
式中:xr(t∈)Rn——参考状态变量;
r(t)——有界参考输入变量;
Ar——稳定矩阵。
采用H∞跟踪控制性能指标[5]:

(3)

Q——正定的加权矩阵;
γ——给定的性能衰减指标。
为处理该系统的跟踪控制问题,选取基于观测器的跟踪控制器模型为:
(4)
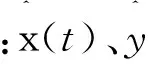
L——需要设计的观测器增益;
K——需要设计的跟踪控制器增益。
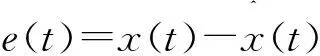

(5)
综合式(1)、式(2)、式(4)和式(5)经过简单的数学处理后可得到闭环系统:
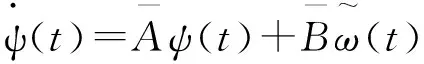
(6)
式中:ψ(t)=[eT(t)xT(t)xrT(t)]T;
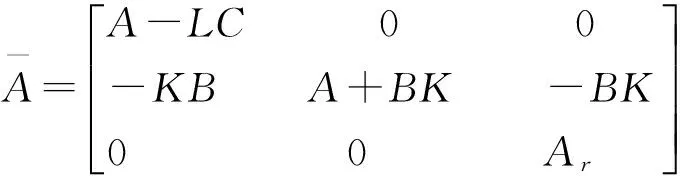

因此,考虑定义ψ(t),H∞跟踪控制性能指标可写成:
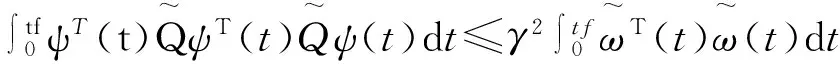
(7)
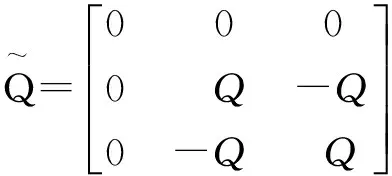
文中的目的是设计控制器 和观测器 ,使得闭环系统式(6)能够满足H∞跟踪控制性能指标。
引理1将被引入到文中的证明过程中。

(1)S<0;
(2)S22<0,S11-S21TS22-1S21<0。
2 控制器设计
基于线性矩阵不等式方法,给出跟踪控制器及观测器的存在条件。
定理1 考虑闭环系统式(6),对于给定的γ>0,如果存在正定矩阵P1,X,P3,以及矩阵Y和Z,使得下述矩阵不等式成立:
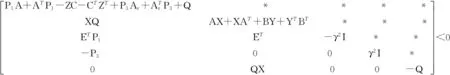
(8)

证明定义如下Lyapunov函数
V(ψ(t))=ψT(t)Pψ(t),P>0,
(9)
对Lyapunov函数式(9)求导可得:
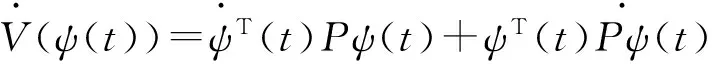
(10)
结合式(3)、式(6)和式(9),以及关系式:
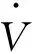
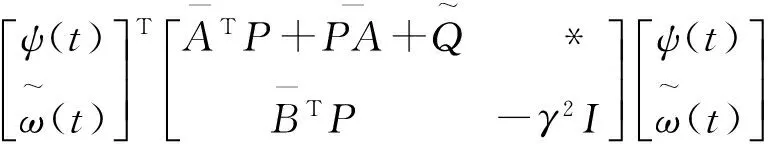
(11)
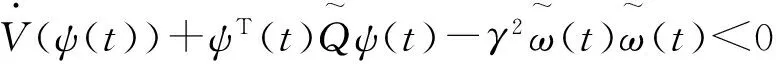
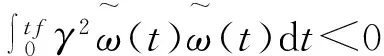
(12)
由于V(ψ(tf))>0,V(ψ(0))=0,故系统的H∞跟踪控制性能指标,可通过式(12)保证。

(13)
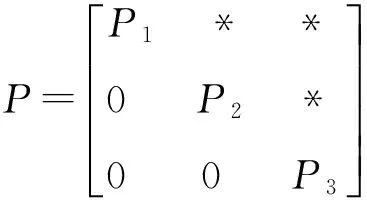
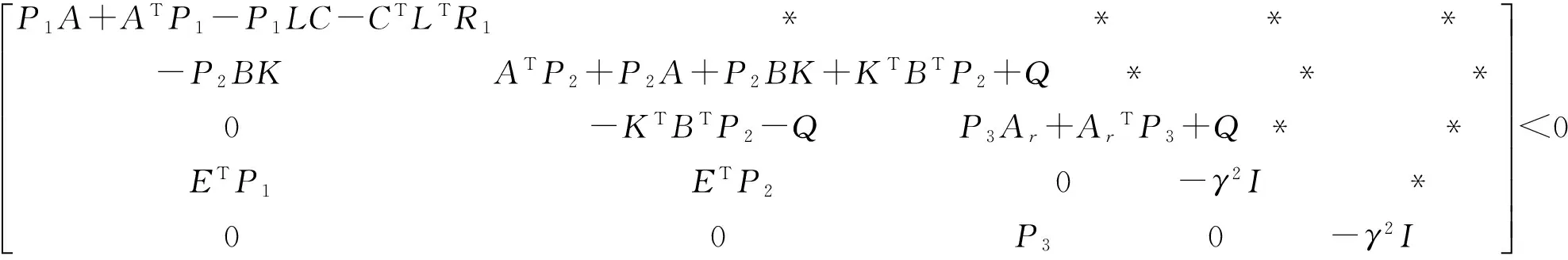
(14)
(15)
3 仿真实例
为实现系统的跟踪控制,选取跟踪参考模型如下:
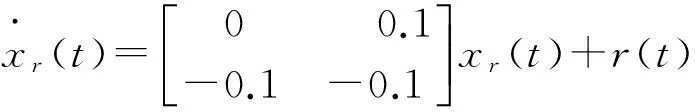
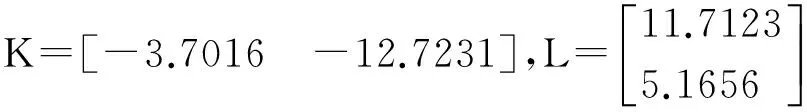
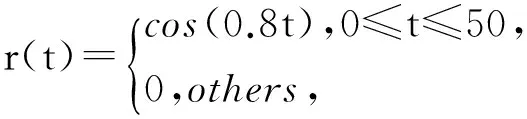

图1 状态变量与参考信号状态变量响应曲线
Fig. 1Statevariableandtimerespondingofreferencesignalstatevariable

图2 状态变量与参考信号状态变量响应曲线
Fig. 2State variable and time responding of reference signal state variable
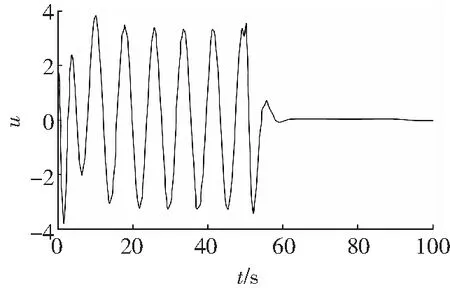
图3 跟踪控制器的输出信号的响应曲线
Fig. 3Time responding of tracking controller output signal
4 结束语
针对线性系统模型,通过线性矩阵不等式(LMI)技术,研究了H∞跟踪控制器设计问题。首先,推导出实现跟踪控制的闭环系统模型,然后,利用Lyapunov函数方法,结合H∞跟踪控制性能指标设计出基于观测器的跟踪控制器存在条件。该存在条件经过一系列矩阵不等式变换方法转化为线性矩阵不等式条件,可通过Matlab软件LMI工具箱求解出跟踪控制器及观测器增益参数。最后,利用数值仿真实例得出结论,闭环系统的状态曲线可有效地跟踪参考信号,进一步证明了定理提出跟踪控制器及观测器设计方法的有效性。
[1]KUNG C C, LI H H. Tracking control of nonlinear systems by fuzzy model-based controller[J]. IEEE International Conference on fuzzy systems 1997, 12(3): 623-628.
[2]YING H. Analytical analysis and feedback linearization tracking control of the general Takagi-Sugeno fuzzy dynamic systems[J]. IEEE transaction on systems, man, and cybernetics, 1999, 29(3): 290-298.
[3]LIN C, WANG Q G, LEE T H. output tracking control for nonlinear systems via T-S fuzzy model approach [J]. IEEE transaction on systems, man, and cybernetics, 2006, 36(2): 450-457.
[4]MANSOURI B, MANAMANNI N, GUELTON K, et al. Output feedback LMI tracking control conditions with criterion for uncertain and disturbed T-S models[J]. Information sciences, 2008, 10 (7): 446-457.
[5]TSENG C S, CHEN B S, UANG H J. Fuzzy tracking control design for nonlinear dynamic systems via T-S fuzzy model [J]. IEEE transaction on fuzzy systems, 2001, 9(3): 381-392.
[6]BOYD S, GHAOUI L E, FERON E, etal. Linear matrix inequalities in system and control theory[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1994.
(编辑李德根)
Design ofH∞tracking controller with linear matrix inequality
FANGHui
(College of Engineering, Bohai University, Jinzhou 121013, China)
This paper introduces the design of tracking controller via linear matrix inequality (LMI), a method designed to improve the tracking control performance of continuous-time linear system. The study using LMI technique and Lyapunov function method and building on tracking controlling parameter as performance index produces the sufficient condition for tracking controller based on observer. The results show that the state response of close-loop system allows
ignals to be tracked, verifying the validity of tracking controller and observer design method.
H∞tracking controller; linear matrix inequality; Lyapunov function
2015-12-08
国家自然科学基金项目(61304149);辽宁省自然科学基金项目(2015020042);辽宁省高等学校杰出青年学者成长计划项目(LJQ2015003)
方辉(1980-),男,实验师,硕士,研究方向:非线性系统控制理论,E-mail:57527060@qq.com。
10.3969/j.issn.2095-7262.2016.01.019
TN911. 7
2095-7262(2016)01-0085-04
A

