带末端角度约束的空地反辐射导弹被动制导律

李　解，雷虎民，李　炯，翟岱亮

(空军工程大学 防空反导学院，西安　710051)



带末端角度约束的空地反辐射导弹被动制导律

李解，雷虎民，李炯，翟岱亮

(空军工程大学 防空反导学院，西安710051)

针对被动跟踪问题，结合UKF和PF滤波各自优点，采用了UPF滤波器对弹目相对运动信息进行了精确估计。针对滤波器估计过程中，对系统状态可观测性的要求，在分析了系统可观测条件的基础上，结合空地反辐射导弹特点，设计了一种带末端角度约束，且能够增强系统状态可观测性的被动制导律。仿真结果表明，UPF滤波器结合所设计的被动制导律能有效准确地估计弹目相对运动信息，实现了精确制导，同时能有效地约束末端攻击角度，保证了空地反辐射导弹的杀伤效果。

末端角度约束；UPF滤波；滑模制导律；被动制导

0　引言

由于空地反辐射导弹仅安装有被动雷达导引头，且仅能测得目标相对导弹的方位角，测角误差大，因此导弹并不能准确获得目标位置信息。在仅有方位测量的情况下对目标进行探测跟踪的问题被称为“被动跟踪”问题，而利用被动跟踪所获得的信息进行制导的问题被称为“被动制导”问题。

对于被动跟踪问题，目前比较常见的是采用卡尔曼滤波器通过纯方位测量对目标信息进行估计。文献[1]采用了EKF滤波器，文献[2]采用了扩张状态观测器，均取得了比较好的估计效果。但是，由于反辐射导弹被动雷达导引头测角误差较大，上述方法估计精度并不能满足制导精度的要求，故本文结合UKF和PF两种滤波器的特点，采用UPF滤波器对目标信息实施估计，在较大的测量噪声下仍可保证滤波精度。

对于空地反辐射导弹被动制导问题，需要考虑两个问题。第一是滤波器的可观测性问题，可观测性反映测量值对系统状态的观测能力，将直接影响估计效果。针对这个问题，文献[3]和文献[4]各自分析了被动跟踪系统的可观测性，提出了导弹适度机动从而提高状态可观测性的观点。第二个问题是满足反辐射导弹打击要求的末端攻击角度约束，这类问题研究成果很多，如文献[5]提出的弹道成型制导律，如文献[6]提出的滑模制导律等等。本文的主要工作是将被动制导问题所涉及的两个问题综合考虑，设计一种即能保证状态可观测性，又保证末端角度约束的空地反辐射导弹被动跟踪制导律。

1　纯方位测量的弹目相对信息估计

在被动制导过程中，弹目相对距离、相对速度等信息需要通过非线性滤波器来估计。综合UKF滤波和PF滤波的特性，本文采用UPF滤波作为弹目相对运动信息的估计手段。

1.1估计系统的建立

静止目标被视为地面上静止不动的质点，其坐标为Xt=[xt，yt，zt]T。

设目标真实坐标为Xt0=[xt0，yt0，zt0]T，则在导弹发射时，由载机装订的目标初始坐标为

(1)

式中ν0为载机雷达观测噪声。

式(1)表明载机装订的目标初始位置带有误差。

设在惯性坐标系中反辐射导弹的坐标为Xm=[xm，ym，zm]T，静止目标雷达的坐标为Xt=[xt，yt，zt]T，选取状态变量为目标雷达对反辐射导弹的相对坐标Xr=[xr，yr，zr]T，即

(2)

系统的状态方程和量测方程可分别描述为

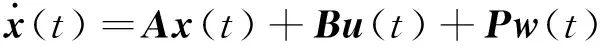
(3)

其中

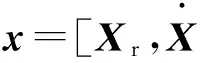
被动导引头的量测模型：

(4)

(5)

(6)

式中θL、ψL为视线倾角和视线偏角；ν1、ν2为被动雷达导引头量测噪声；Xr=Xt-Xm=[xr，yr，zr]T。

1.2UPF滤波算法

Bayes估计理论所推导出的时间更新方程和测量更新方程是一种最优估计。其方程形式虽然简单，但是一个高维积分方程，一般并不能显式地表达出来。

针对非线性系统，主流的Bayes估计数值计算方法分为高斯假设参数化方法的非线性卡尔曼滤波EKF和UKF，以及贯序蒙特卡洛方法的粒子滤波PF。

非线性卡尔曼滤波中，EKF通过对非线性系统状态方程和测量方程进行一阶泰勒展开，将非线性问题转化为线性问题，当系统非线性较强时，滤波稳定性和精度将大幅度下降。UKF通过对无迹变换(Unscented Transform)，在假设状态高斯分布的前提下，对状态进行sigma采样，从而近似状态的概率密度分布，具有良好的非线性和滤波精度。

故本文结合UKF和PF的优点，利用UKF代替建议分布进行重要性采样，即利用UKF来预测下一个粒子，每个粒子的建议分布如下：

(7)

UPF的计算过程如下：

(1)初始化

从先验概率分布p(x0)中抽取N个粒子：

(8)

(9)

(2)重要性采样

通过建议分布：

(10)

计算重要性权值：

(11)

并归一化：

(12)

(3)重采样

重采样过程依据重要性权值，复制权值大的粒子，丢弃权值较小的粒子，以消除粒子的退化现象，使其分布符合状态转移概率分布的变化。粒子复制完毕后，赋予每个粒子等权值：

(13)

(4)状态输出

(14)

状态均值：

(15)

2　被动跟踪系统可观测性分析

空地反辐射导弹被动跟踪依赖滤波器对弹目相对运动信息的估计，滤波效果对导弹能否实现精确制导显得尤为重要。滤波效果的好坏，除了与滤波器本身性能和导引头噪声大小有关外，还取决于被动跟踪系统的可观测性强弱。

被动跟踪系统的测量是非线性的，而非线性系统的可观测性如下定义：

当存在有限时刻t>t0时，若其Grammian矩阵：

D(t，t0)=∫t0tΦT(t，t0)HT(t)H(t)Φ(t，t0)dt

(16)

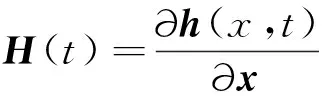
根据式(3)求得被动跟踪系统的状态转移矩阵：

(17)

根据式(4)求被动跟踪系统的测量矩阵其形式复杂，现将式(4)进行线性化：

(18)

令

(19)

再对M0(t)进行变换，推导出：

(20)

则非线性测量模型可写成如下线性形式：

(21)

对于式(3)和式(21)所描述的系统，若系统在时间区间(t0，t)上状态是可观测的，则其Grammian矩阵：

D(t，t0)=∫t0tΦT(t，t0)MT(t)M(t)Φ(t，t0)dt

(22)

是正定的。其等价描述是，矩阵M(t)Φ(t，t0)的列向量线性无关[8]。

任取列向量α=[a1，a2，a3，a4，a5，a6]T，ai不全为0，若M(t)Φ(t，t0)的列向量线性无关，则

(23)

将α带入式 (23)，得

(24)

(25)

考虑式(21)，得

(26)

(27)

由系统状态方程，可得

(28)

(29)

结合式(26)～式(28)，得

(30)

若上式成立，则式(23)成立，即M(t)Φ(t，t0)的列向量线性无关。此时，系统的Grammian矩阵D(t，t0)正定，系统是可观测的。

而式(3)中：

(31)

式中θvm、ψvm为弹道倾角和弹道偏角；amy、amz为导弹在俯仰平面和偏航平面的加速度。

若式(30)成立，则

(32)

进而推得

(33)

从上式可得出结论，若要使滤波器在导弹制导过程具有良好的估计精度，则制导过程中要保持一定的视线角变化率。

3　带末端角度约束的滑模制导律设计

本文考虑到空地反辐射导弹末制导对末端角度约束的要求以及滤波器可观测性的要求，参考文献中运动跟踪滑模制导律的思想[9]，设计一种既保证末端角度约束，又保证视线角变化的制导律。

3.1三维弹目相对运动模型

弹目相对运动关系如图1所示。

图1　弹目相对运动关系

图1中，xiyizi为惯性坐标系；xLyLzL为视线坐标系；xvyvzv为弹道坐标系；m为导弹；t为目标；θL、ψL分别为视线倾角和视线偏角；θm、ψm分别为导弹相对视线坐标系的倾角和偏角。

设导弹的速度为Vm，amy和amz分别为导弹在俯仰平面和偏航平面的加速度，目标视为地面静止目标，弹目相对距离为r。

由图1可得

(34)

(35)

(36)

(37)

(38)

对式(35)、式(36)求导结合式(37)、式(38)得

(39)

(40)

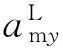
3.2俯仰平面制导律设计

考虑制导律设计对末端角度约束及状态可观测性的要求，令

(41)

(42)

选取滑模面为

s=k1|x1|γsgn(x1)+k2x2

(43)

参数k1>0，k2>0，0<γ<1。

根据滑模变结构控制理论，为保证系统状态平稳接近滑模面进入滑动模态，采用趋近律方法推导制导律。选取趋近律：

(44)

由式(43)、式(44)，可得

(45)

由于r>0，所以

(46)

根据滑模变结构控制理论，系统状态将在有限时间内到达滑模面。

对式(43)求导：

(47)

由式(46)，可得

(48)

将式(39)带入式 (48)，可得

(49)

从而推得制导律：

(50)

(51)

(52)

(53)

(54)

(55)

3.3偏航平面制导律设计

偏航平面制导律设计不考虑末端角度约束，为保证整个制导系统的稳定性，偏航平面制导律的设计基于零化视线角速率的思想设计。

令

(56)

选取滑模面：

s=x3

(57)

选取趋近律：

(58)

参数k3>0，0<α3<1。则根据式(40)和式(58)可推导出偏航平面制导律：

(59)

所需制导信息同样由滤波器估计获得。

4　仿真分析

UPF滤波器粒子数N=100，协方差阵初值取P0=diag(1002，102，1002，102，102，102)，过程噪声方差cov(ω)=0.0012，测量噪声方差cov(ν)=2.25(°)2。

为对比验证，仿真中采用3种带末端角度约束的制导律，分别为本文所设计的制导律，文献[5]所述的弹道成型制导律(TSG)，文献[6]所述的滑模制导律(SMG)。3种制导律作用下滤波器对弹目相对坐标的估计误差如图2所示。

(a)本文设计的制导律

(b)TSG

(c)SMG

从图2(a)可看出，目标位置X坐标、Y坐标、Z坐标均能准确收敛。

图2(b)、(c)与图2(a)相比，无论是TSG还是SMG，其估计收敛效果均不如本文所设计的制导律。因为滤波器估计效果好坏的关键就在于系统可观测性的强度，而本文所设计的制导律可有效提高系统的可观测性，故效果优于其他两种制导律，制导精度也进一步提高。制导精度对比见表1。

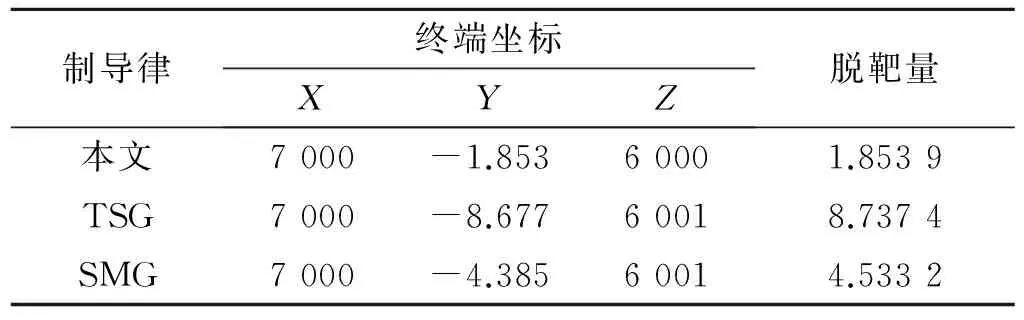
表1　3种制导律制导精度对比

图3～图5是滤波器对视线倾角、视线偏角和弹目相对速度等制导律所需信息的估计误差。由图可看出，3种信息误差均迅速收敛，保证了制导指令的准确性。

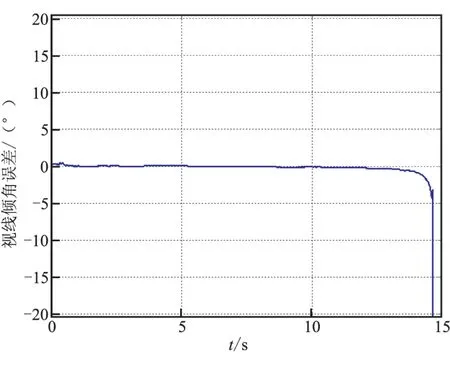
图3　视线倾角误差

图4　视线偏角误差

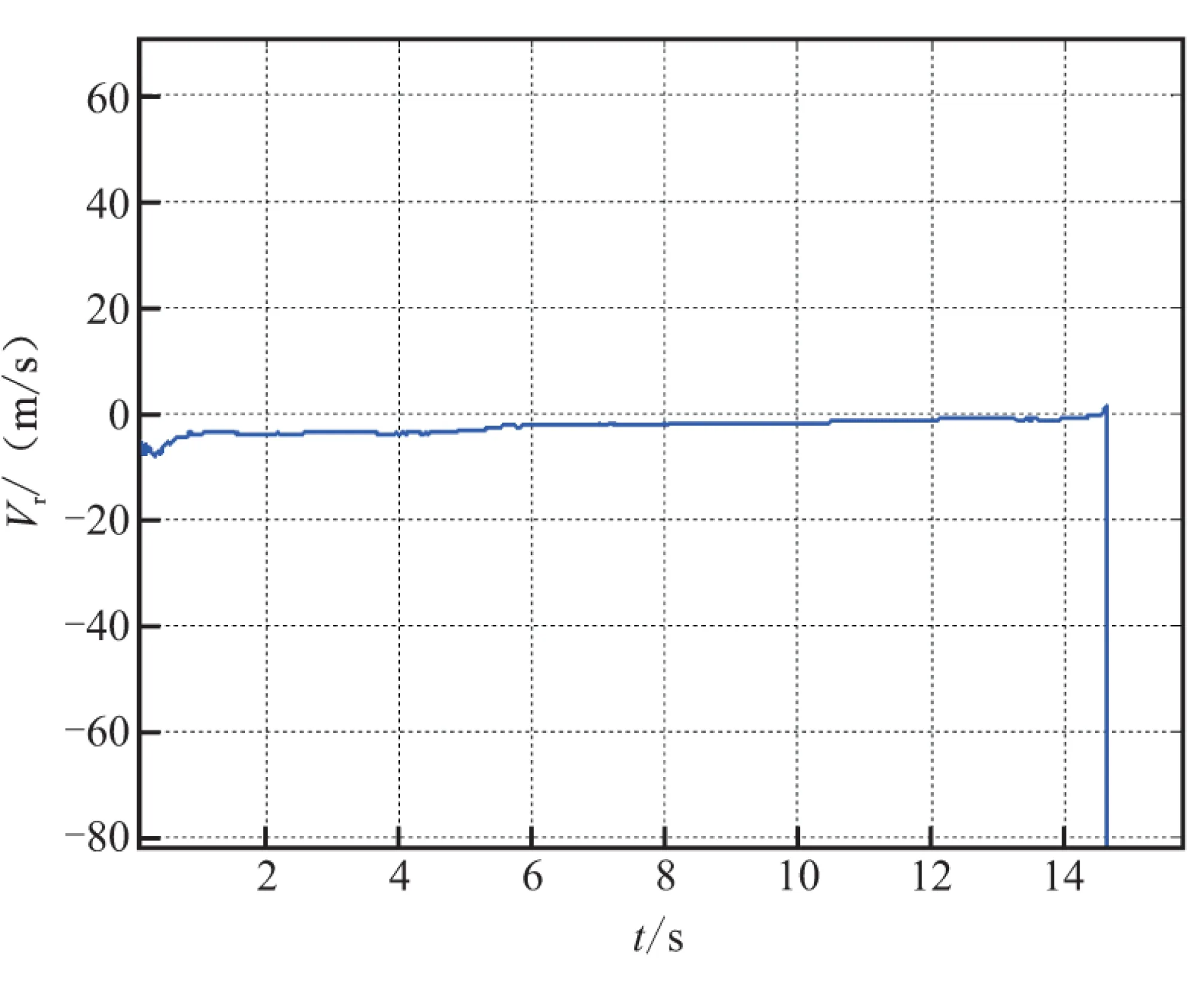
图5　相对速度误差

图6反映视线倾角的变化，从图6可看出，在给定末端角度约束为-80°的情况下，所设计制导律可保证导弹以期望角度攻击目标。图7反映视线倾角速率随时间的变化，由图7可见，视线倾角速率能够按照期望的视线倾角速率运动，从而保证了系统的可观测性，即保证了滤波器状态估计的准确性。

图6　视线倾角

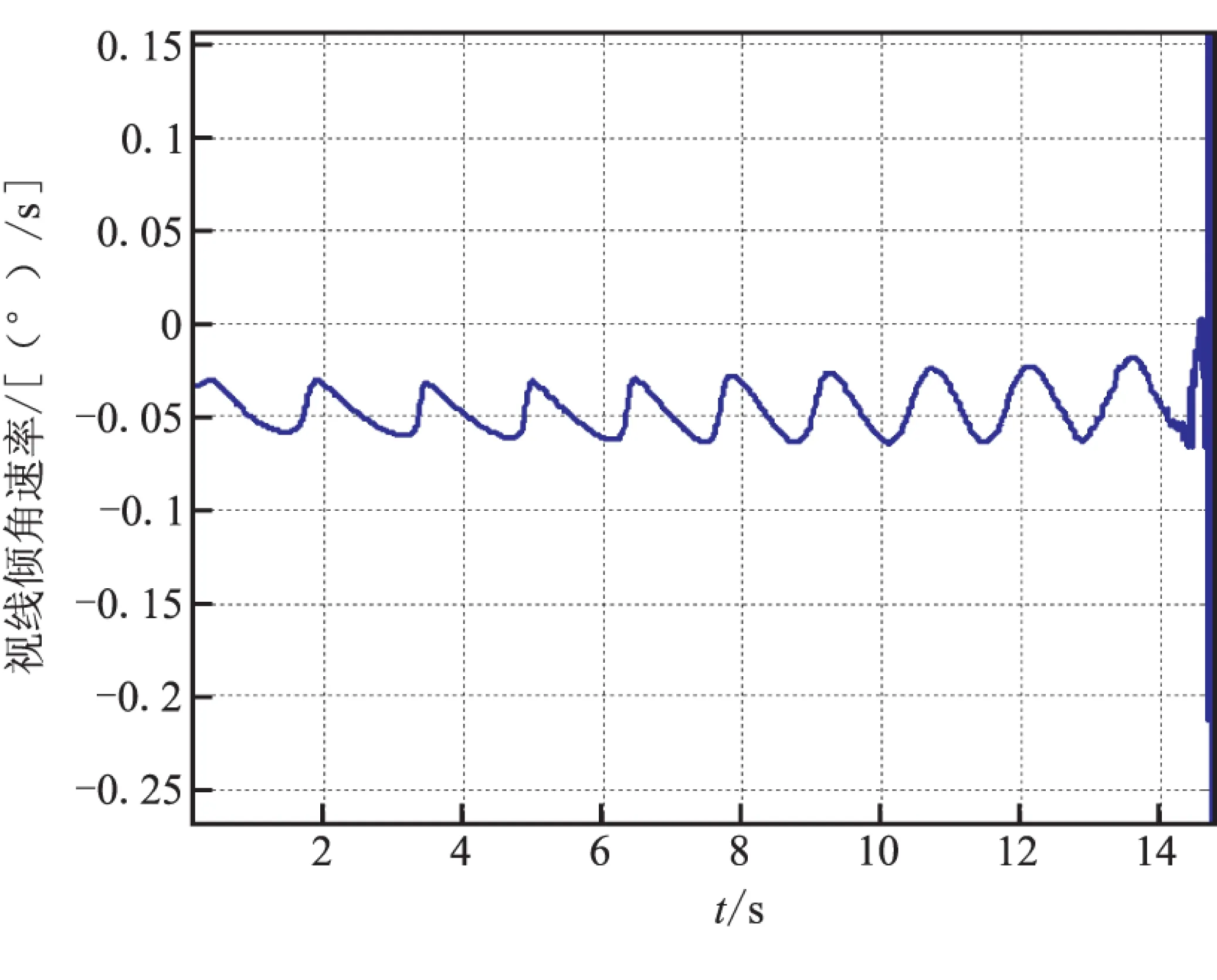
图7　视线倾角速率

5　结论

(1)本文结合UKF和PF滤波器各自的特点，采用UPF滤波器对被动制导过程中所需的弹目相对信息进行估计，在所设计制导律的配合下，获得了良好的估计效果。

(2)本文在分析了系统可观测性的基础上，设计了能够有效保证系统可观测性的制导律，从而保证了滤波器的估计精度。针对空地反辐射导弹的特殊性，所设计的制导律还能同时对末端角度起到良好的约束作用，保证了杀伤效果。

[1]魏玉乐,方群,罗建军.弹目信息在纯方位制导中的应用[J].西北工业大学学报,2005 ,23(5).

[2]马克茂.带有终端视线约束的非光滑制导律设计[J].弹道学报,2011,23(2).

[3]田宏亮,梁晓庚,贾晓洪,等.基于视线角速度的增强目标可观性研究[J].弹道学报,2011,23(2).

[4]杨国胜,窦丽华,候朝桢.基于纯角度的三维运动目标可观性研究[J].兵工学报,2004,25(2).

[5]Paul Zarchan.Tactical and strategic missile guidance 6th edition [M].American Institute of Aeronautics and Astronautics,Inc.

[6]尹永鑫,杨明,吴鹏.针对机动目标带攻击角约束的三维制导律[J].固体火箭技术,2010,33(3).

[7]Julier S J,Uhlmann J K.Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE,2004,92(3).

[8]Lim C C,Li M.Observability analysis of two closed-loop guidance systems with bearings-only measurements[J].Nonlinear Analysis:Real World Applications 1,2000.

[9]周荻.寻的导弹新型导引规律[M].北京:国防工业出版社,2002.

(编辑：吕耀辉)

Passive guidance law for air-to-ground anti-radiation missile with terminal angular constraint

LI Jie，LEI Hu-min，LI Jiong，ZHAI Dai-liang

(Air Force Engineering University Air and Missile Defense College，Xi’an710051，China)

For passive tracing problem,combined with the advantages of UKF and PF filters,an UPF filter was adopted to realize the accurate estimation of the information of missile-target relative movement.For the requirement of the observability of system states during estimating,combined with the characteristic of air-to-ground anti-radiation missile,a passive guidance law with terminal angular constraint and observability enhancement was designed.The simulation result shows that the UPF filter combined with the designed passive guidance law can estimate the relative information accurately and effectively and realize accurate guidance.Meanwhile, with effective terminal angular constraint,the damage effect of the missile is guaranteed.

terminal angular constraint；UPF filter；sliding mode guidance；passive guidance

2015-05-23；

2015-06-15。

航空科学基金(20140196004)；航空科学基金(20130196004)。

李解(1991—)，男，硕士生，研究方向为空天拦截器制导、控制与仿真。E-mail：sumffuk@163.com

V448

A

1006-2793(2016)04-0594-07

10.7673/j.issn.1006-2793.2016.04.026