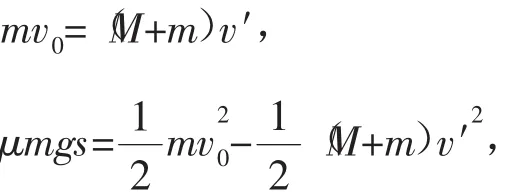巧用对称性解力学题
安徽省灵璧黄湾中学 华兴恒
巧用对称性解力学题
安徽省灵璧黄湾中学 华兴恒
许多物理模型、物理现象、物理规律中都存在着和谐而优美的对称性。在解题过程中,如果我们能够巧妙而灵活地运用对称性,常常可以避免复杂的数学运算和推导过程,直接抓住问题的本质,出奇制胜,使一些复杂的问题变得简单。
一、平衡位置对称
对有关平衡位置对称的问题,应注意相关物理量在对称位置处的大小关系,并在解题过程中加以利用。
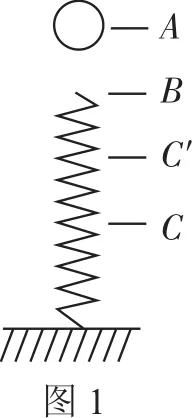
例1如图1所示,小球自A点静止自由下落,到B点时与弹簧接触,到C点时弹簧被压缩到最短,若不计弹簧的质量与空气阻力,则小球在C点的加速度a______g(选填“>”、“=”或“<”)。
解析这是一道同学们感到较为棘手的问题,因为无法定量分析小球在C点受到的弹力大小。如果我们适当转换一下思维的角度,改让小球无初速度从B点释放,设小球在BC′间做简谐振动。依据简谐振动的对称性可知,小球在B点与C′点的加速度大小相等(两个最大位移处),且均等于g。那么当小球从A处落下时,小球所能到达的最低点C低于C′点,因此小球在C点受到的弹力大于在C′点受到的弹力,所以小球在C点的加速度大于g。
二、时间变换对称
系统在时间反演变换下,即t→-t的变换下具有的不变性,称为时间反演对称,时间反演如同时光倒流,在真实世界中是不可能发生的,但可以通过一对相对的过程来模拟演示。例如,对于竖直方向的抛体运动,由于速度具有对称性,因此相应的时间也具有对称性。在解题的过程中,如果能够灵活地运用这种对称性,可以极大地简化解题过程。
例2一个人在离地H高度处以相同的速率v0同时抛出两个小球A和B,A被竖直上抛,B被竖直下抛,不考空气阻力等因素,两球落地时间差为Δt,求速率v0。

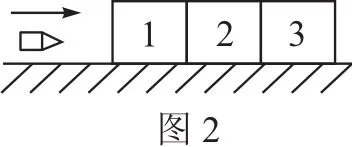
例3有三块材料相同、形状相同的长方体木块,并排固定在水平地面上,如图2所示。现有一子弹以水平速度v0射入木块中,且射入第三块后刚好没有射出来,求子弹在三块木块中运动的时间之比。(不考虑重力的影响)
解析子弹射入木块后与各个木块之间的摩擦力不变,根据牛顿第二定律可知,子弹在各个木块内的加速度也不变。由运动学知识可知,子弹在木块内做初速度不为零的匀减速运动,直到射入第三块并刚好没有射出来。由于加速度相同的匀减速运动与匀加速运动具有对称性,所以子弹在木块内的匀减速直线运动,也可以看作由第三块木块开始的初速度为零的匀加速直线运动。
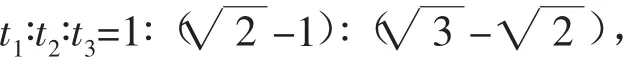
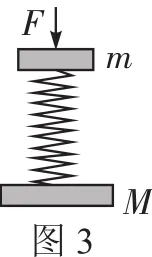
例4用一轻弹簧把两块质量分别为M和m的木板连接起来,放在水平地面上,如图3所示。则必须在上板上施加多大的压力F,才能使F撤去后,上板弹起来后恰好能使下板离地?
解析本题若采用能量守恒的观点求解,将非常繁杂。考虑到简谐运动具有时间反演对称性,则可将上面的木板的运动看作弹簧振子,利用对称性求解,将会非常简捷。
假设拉力F′作用在上板上,欲使M离地,拉力F′至少为(M+m)g。根据弹簧的拉伸与压缩过程具有对称性,要产生相同的效果,作用在上板的压力F至少应为(M+m)g。
三、镜像对称
镜像对称是一种空间反演,物体在平面镜中成像时,物与像总是关于镜面对称的。某些物理问题也常具有这样的对称性。如果我们能够抓住这一特征,并对问题进行迁移或变换,常能起到化难为易的作用,达到简捷求解的目的。
例5如图4,相对的两个斜面,倾角分别为37°和53°,在顶点把两个小球A、B以同样大小的初速度分别向左、右水平抛出,小球都落在斜面上,若不计空气阻力,则A、B两小球运动的时间之比为()。
A.1∶1B.4∶3C.16∶9D.9∶16
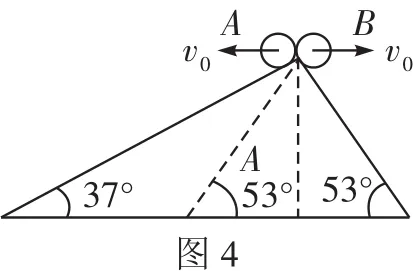
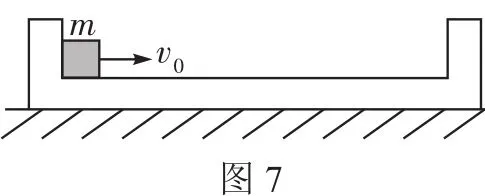
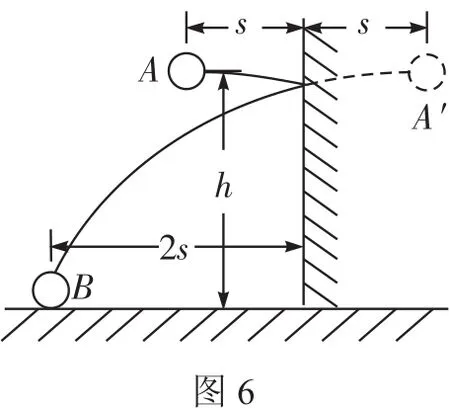
解析如图4所示,作出53°倾角斜面在左侧的对称面。设想A、B两球都以v0水平向左抛出,显然B球在碰到53°倾角斜面之前必定先碰到37°倾角斜面,故tA 评析这是一道典型的灵活运用镜像对称法,化不对称为对称的例子。乍一看,本题似乎并不具有对称性,但当作出53°倾角斜面的对称面后,问题的求解便变得非常明朗、清晰了。 例6如图5所示,玻璃球A离地面高度H=5 m,跟竖立钢板MN相距s=2 m。让A球以v0=5 m/s的初速度水平抛出,跟MN做弹性碰撞后落回到地面,求落地点C与MN的距离L。 解析此题采用常规解法比较烦琐,若采用镜像对称法求解则非常简捷。把MN当作“平面镜”,作出A球轨迹BC的“像”BC′,因BC′与BC关“镜面”MN对称,且碰撞中没有机械能损失,故曲线ABC′是球A做平抛运动的完整轨迹。 例7沿水平方向向一堵竖直光滑的墙壁抛出一个弹性小球A,抛出点离水平地面高为h,距墙壁的水平距离为s,小球与墙壁发生弹性碰撞后,落在水平地面上,落地点距墙壁的水平距离为2s,如图6所示。求小球抛出的初速度。 解析因小球与墙壁发生弹性碰撞,所以小球与墙壁碰撞前后入射速度与反射速度具有对称性,碰撞后小球的轨迹与无墙壁阻挡时,小球继续前进的轨迹对称,如图6中所示。故此小球的运动可以转换为平抛运动来处理,效果相当于从A′点(A点关于墙壁的对称点)抛出。 对称性的思维方法,除了可以直接应用于具有对称性的物理问题外,还可以拓展开来,应用于一些隐含着对称思想的问题。 例8质量为M的盒子放在光滑的水平面上,如图7。盒内有一质量为m的小木块(可视为质点)以速度v0从左往右运动,木块与盒子间的动摩擦因数为μ,若盒子长度为L,木块与盒壁发生多次碰撞,且碰撞时无动能损失,求木块与盒壁共能发生多少次碰撞。 解析本题涉及木块与盒壁的多次碰撞,由于盒内摩擦力的作用,盒子与木块同时有运动,题目设置的情境比较复杂,使得初次接触此类问题的同学感到难以入手。但是由于条件中有“碰撞时无动能损失”,因此可将碰撞时的盒壁当作“平面镜”,将木块与盒壁碰后的运动“反映”到其“像”上,把问题转化为一个“具有足够长的盒子,求木块在盒内的位移”问题,而这个问题就是典型的子弹射木块问题,运用动量守恒定律和动能原理便可简捷求解。 从以上几例可以看出,运用对称性分析解决问题,不仅能使问题的求解变得流畅而简捷,同时还能提高思维的创造性和深刻性,使同学们在解决问题的过程中享受到成功的喜悦,增强学习物理知识的兴趣。 同学们在学习物理知识的过程中,不仅要掌握知识,还要掌握正确的解题思想方法,提高思维的灵活性、敏捷性与创造性,加强各种思维方法的训练,这样不仅可以提升思维品质,优化思维过程,而且还可以提高思维能力。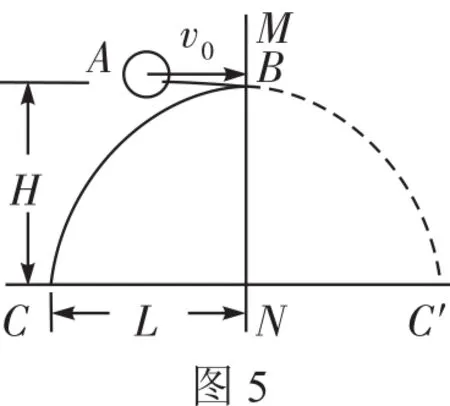
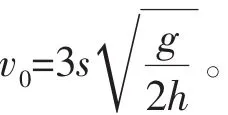
四、拓展应用