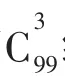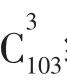解决排列组合中分组与分配问题的一类重要模型——『小球入盒』模型

安徽省宿州二中 凤斌 叶菊

解决排列组合中分组与分配问题的一类重要模型——『小球入盒』模型

安徽省宿州二中 凤斌 叶菊

数学建模是一种数学的思考方法，是运用数学的语言和方法，通过抽象、简化，建立能近似刻画并“解决”实际问题的数学模型的一种强有力的数学手段。排列组合问题的情景设置千变万化，“小球入盒”是一类典型的数学模型，将其用来解读排列、组合问题，可以搭起挖掘知识的内涵和外延的平台，直击目标。

一、不同小球入不同盒子问题

模型1（球少盒多）5个不同的球，放入8个不同的盒子中，每盒至多放1个球，共有多少种放法？

（方法二）由于每盒至多放1个球，所以第1个球有8种放法，第2个球有7种放法，…，第5个球有4种放法。因此，完成这件事有8×7×6×5×4=6720种方法。

模型2（球多盒少）（1）4个不同的球，放入3个不同的盒子，每个盒子至少放1个球，共有多少种放法？

（2）6个不同的球放入4个不同的盒子，每个盒子至少放1个球，共有多少种放法？

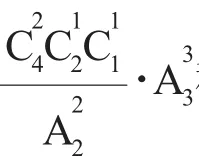
例1某体育赛事中，需要英语、法语、德语、意大利语4种语言翻译各1名，现可从3个学校中选取，每个学校至少1名，共有多少种选法？

解析把4个名额看成4个不同的小球，分配到的3个学校当作3个不同的盒子。这个问题就转化为我们模型2的第（1）题了。

二、相同小球入不同盒子问题

模型3（球少盒多）5个相同的球，放入8个不同的盒子中，每盒至多放1个球，共有多少种放法？

模型4（球多盒少）（1）6个相同的球，放入4个不同的盒子中，每盒至少放1个球，共有多少种放法？

（2）4个相同的球，放入3个不同的盒子中，共有多少种放法？

（3）8个相同的球放入3个盒子中，每个盒子至少放2个，共有多少种放法？

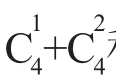
说明：“至少一个”是利用“隔板模型”处理问题的特定情境。

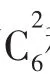
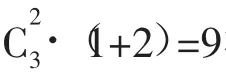
显然，方法一较方法二要简单。

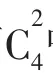
例2学校现在有6个青年志愿者的名额，分配到高一的4个班级，每个班级至少1个名额，共有多少种分配方案？

解析把6个名额看成6个相同的小球，分配到的4个班级当作4个不同的盒子。这个问题就转化为我们模型4的第（1）题了。

例3（1）求方程X+Y+Z+W=100共有多少组正整数解。

（2）求方程X+Y+Z+W=100共有多少组非负整数解。