柯西不等式要点解读

安徽省太和中学　岳峻

柯西不等式要点解读

安徽省太和中学岳峻

柯西不等式是由大数学家柯西发现的经典不等式，它不仅具有简洁、对称的数学美感，而且具有重要的应用价值。灵活巧妙地运用柯西不等式，可以使得一些较难解决的问题迎刃而解。

如何破解柯西不等式应用的关键点呢？解题者应立足于已知信息和待求（证）式结构的特征，敏锐地捕捉到这些关键结构，并对这些结构进行分析，分析常量与变量之间的关系，加以思考、处理，灵活应对。

一、二维形式的柯西不等式

（1）若a、b、c、d都是实数，则（a2+b2）（c2+d2）≥（ac+bd）2，当且仅当ad=bc时，等号成立。

（2）（向量形式）设α、β是两个平面向量，则|α·β|≤|α||β|，当且仅当β是零向量，或存在实数k，使α=kβ时，等号成立。

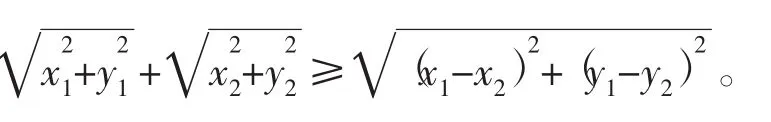
（4）（三角不等式Ⅱ）若x1、y1、x2、y2、x3、y3∈R，

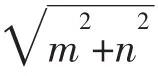
分析二维形式的柯西不等式（a2+b2）（c2+d2）≥（ac+bd）2的左边是的结构，而右边是的结构，即，已知信息a2+b2=5，ma+ nb=5中的代数式ma+nb为乘积之和，具有柯西不等式右边代数式的结构，而已知信息中的代数式a2+b2与待求最值的代数式显然都含有平方和，具有柯西不等式左边两个代数式的结构，因此令即可。

解析由柯西不等式得（a2+b2）（m2+n2）≥（ma+nb）2，当且仅当an=bm时，等号成立。

点评 在运用柯西不等式时，我们要着眼于已知信息与待解（证）式的结构特点，构造出柯西不等式的形式。

例2已知x、y∈R，3x2+2y2≤6，求2x+y的最值。

解析由柯西不等式可得：

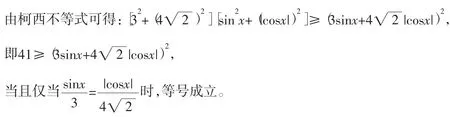
点评 本例展示了柯西不等式的变形应用。柯西不等式是一个十分重要的解题工具，在应用时，我们要善于构造出柯西不等式的形式，配凑系数，合理变化关系式，并注意等号成立的条件。

二、三维形式的柯西不等式

（1）若a1、a2、a3、b1、b2、b3都是实数，则，当且仅当bi=0（i=1，2，3）或存在实数k，使ai=kbi（i=1，2，3）时，等号成立。

（2）（向量形式）设α、β是两个空间向量，则|α·β|≤|α||β|，当且仅当β是零向量，或存在实数k，使α=kβ时，等号成立。

例4设x、y、z∈R，若x-2y+z=4。

（1）求x2+y2+z2的最小值。

（2）求x2+（y-1）2+z2的最小值。

（1）已知信息x-2y+z=4中的x-2y+z可以视为乘积之和，

即1×x+（-2）×y+1×z，具有柯西不等式右边代数式的结构，

待求最值的代数式x2+y2+z2显然是平方和的结构，具有柯西不等式左边代数式之一的结构，

因此，可令■=x，●=y，▲=z，

而已知信息x-2y+z=4中，x、y、z的系数分别为1、-2、1，

相应的，令□=1，○=-2，△=1，

所以，［12+（-2）2+12］（x2+y2+z2）≥［1×x+（-2）×y+1×z］2，

即6（x2+y2+z2）≥（x-2y+z）2=16，

（2）待求最值的代数式x2+（y-1）2+z2显然也是平方和的结构，具有柯西不等式左边代数式之一的结构，

而已知信息x-2y+z=4中，x、y、z的系数分别为1、-2、1，

相应的，令□=1，○=-2，△=1，

所以，［12+（-2）2+12］［x2+（y-1）2+z2］≥［1×x+（-2）×（y-1）+1×z］2，

即6［x2+（y-1）2+z2］≥（x-2y+z+2）2=36，

故x2+（y-1）2+z2≥6，

当且仅当x=z=1，y=-1时，等号成立。

所以x2+（y-1）2+z2的最小值为6。

点评我们在运用柯西不等式时，不仅要注意它的数学意义，还要注意它的外在形式。当一个代数式与柯西不等式的左边或右边具有一致的形式时，就可以考虑利用柯西不等式对这个式子进行缩小或放大。

例5%设a、b、c∈R*。

解析%（1）由柯西不等式，得

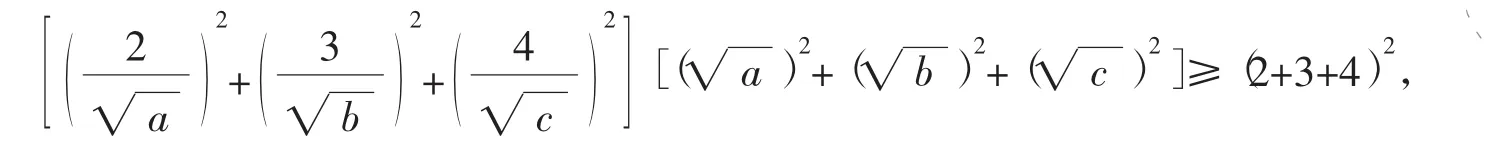
（2）由柯西不等式，得

三、n维形式的柯西不等式