平面向量数量积的几种基本求法
安徽省铜陵一中 钟永庆
平面向量数量积的几种基本求法
安徽省铜陵一中 钟永庆
近几年来,平面向量数量积的求解问题在高考选择题、填空题中出现的频率较高,甚至出现在解答题中,我们应予以足够的重视。本文结合几道典型例题谈谈如何求平面向量的数量积,希望对大家有所启发。
一、定义法
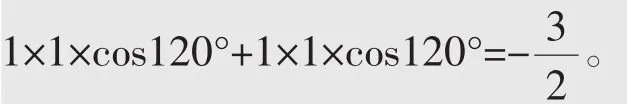

例2已知a、b、c均为单位向量,且|a+b|=1,则(a-b)·c的取值范围是()。
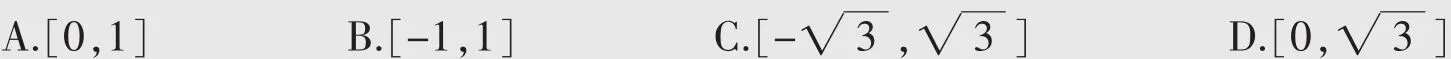
二、坐标法
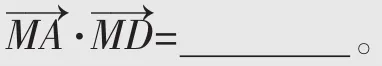
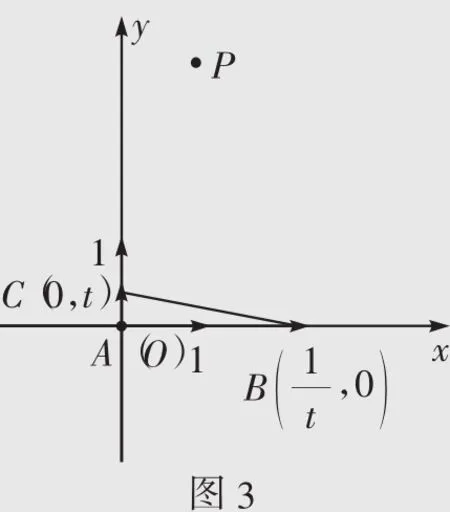
解析如图2,以A为坐标原点,以AB、AD所在直线为x轴、y轴建立直角坐标系,由题意知,
总而言之,写作是一项综合技能,离不开遣词造句、谋篇布局,每个环节都很重要。英语写作能力的提高也不可能一蹴而就,是一个长期积累、逐步提高的过程,需要平时大量的练习。只要我们循序渐进、持之以恒,我们的英语写作水平就一定会不断提高。

解析依题意,以A为坐标原点,以AB、AC所在直线为x轴、y


点评平面向量的坐标运算:若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2。用坐标法解决数量积问题,必须先建立适当的直角坐标系,用坐标表示出相应的点和向量,再利用坐标运算公式进行计算。如果题中涉及一些较为规则、对称的图形时(如等边三角形、矩形等),此法往往会给我们的计算带来极大的方便。
三、基向量法
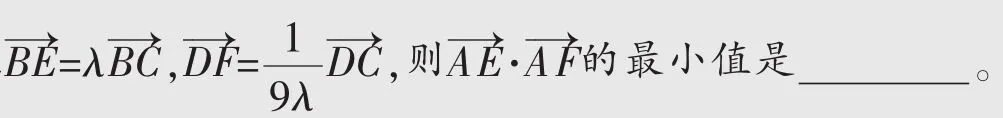


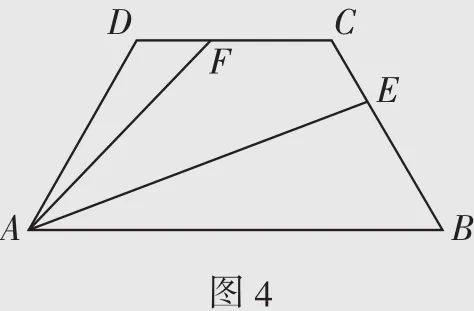
例6如图5,在Rt△ABC中,已知斜边BC=a,若长为2a的线段PQ以点A为中点,则PCCQ与BCCC的夹角θ取何值时BCCP·CCCQ的值最大?求出这个最大值。

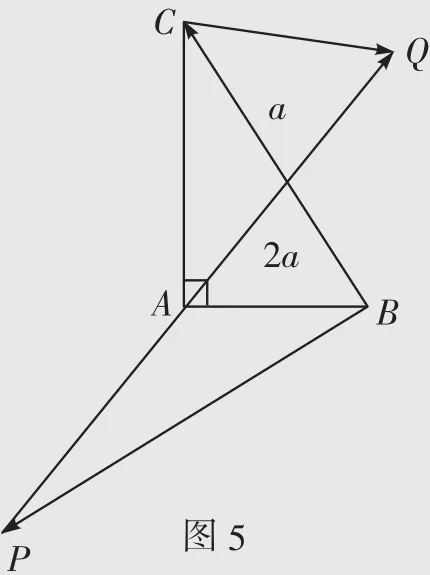
点评求向量a、b的数量积时,若a、b的模和夹角都不容易求出来,且题中所给的平面图形不适合建立坐标系时,可以考虑此法。依据平面向量基本定理,用其他已知或很容易求出模和夹角的向量来表示a、b(即选定一组基底,其他向量都用基底表示),再进行相应的线性运算,从而解决问题。
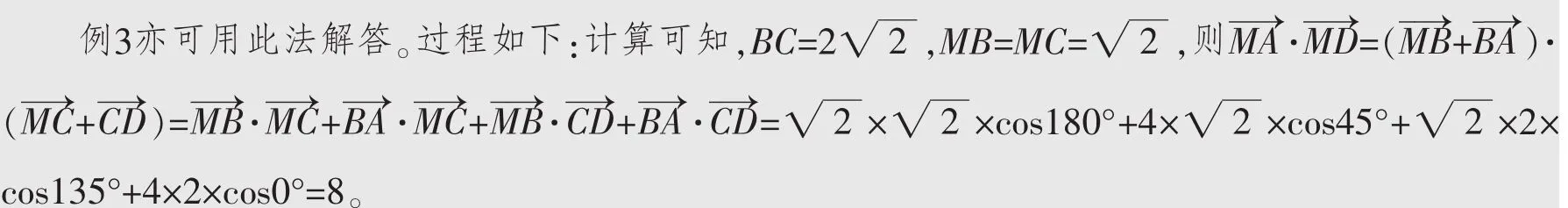
点评事实上,坐标法是基向量法的特例,已知a=(x1,y1)=x1i+y1j,b=(x2,y2)=x2i+y2j,其中i、j是单位正交基底(即两个相互垂直的单位向量),
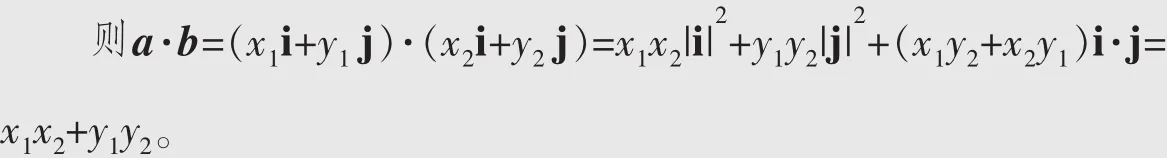
四、几何意义法
A.2B.4C.6D.8
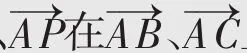

点评向量数量积的几何意义:数量积a·b等于a的模与b在a方向上的投影|b|cosθ的乘积。如果我们能找到一个向量在另一个向量方向上的投影,采用这种方法能大大减少计算量。
练习
1.已知a、b为单位向量,其夹角为60°,则(2a-b)·b=。

3.已知i、j、k表示共面的三个单位向量,i⊥j,那么(i+k)·(j+k)的取值范围是()。
A.[-3,3]B.[-2,2]

4.已知△ABC是边长为2的正三角形,点P为△ABC内一点,且P△△A+2P△△B+3P△△C=0,则P△△A·P△△B=()。

参考答案