具有潜伏期的两组传染病模型的稳定性研究

冯晓梅，王翠花，卢永红

（运城学院应用数学系，山西运城044000；山西大同大学数学与计算机科学学院，山西大同037009）

具有潜伏期的两组传染病模型的稳定性研究

冯晓梅1，王翠花1，卢永红2

（运城学院应用数学系，山西运城044000；山西大同大学数学与计算机科学学院，山西大同037009）

在文中，研究了一类具有潜伏期的两组传染病动力学模型,通过对模型的理论分析，结论显示：当R0≤1时，该模型的无病平衡点是全局渐近稳定的。

基本再生数;Lyapunov函数;全局稳定性

对于具有潜伏期的传染病模型近年来已经有很多学者做了研究【1-3】。传染病模型研究如下：

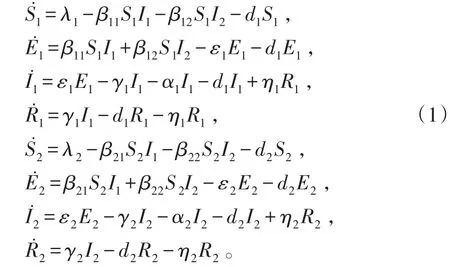
是模型（1）的正向不变集，用Ω∘表示Ω的内部。因此，我们在不变集Ω中讨论模型（1）的解。

1 基本再生数

其中：

根据文献[4]，可以得到：

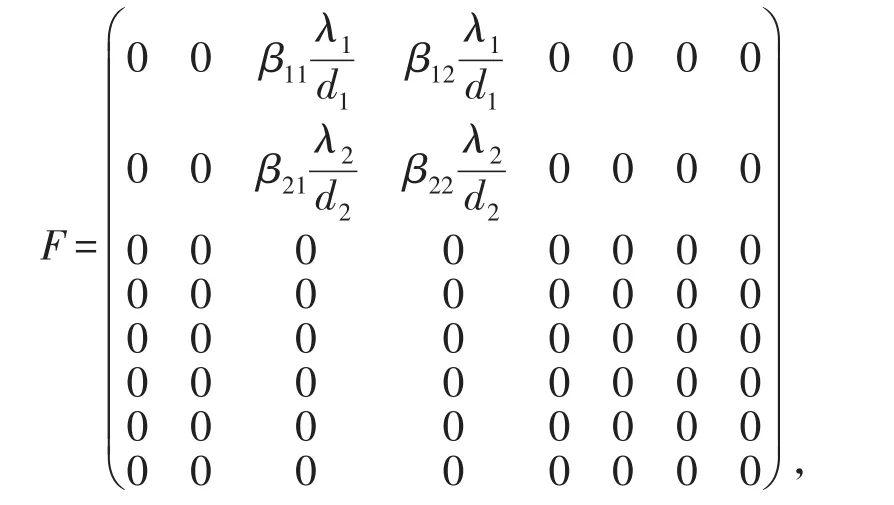
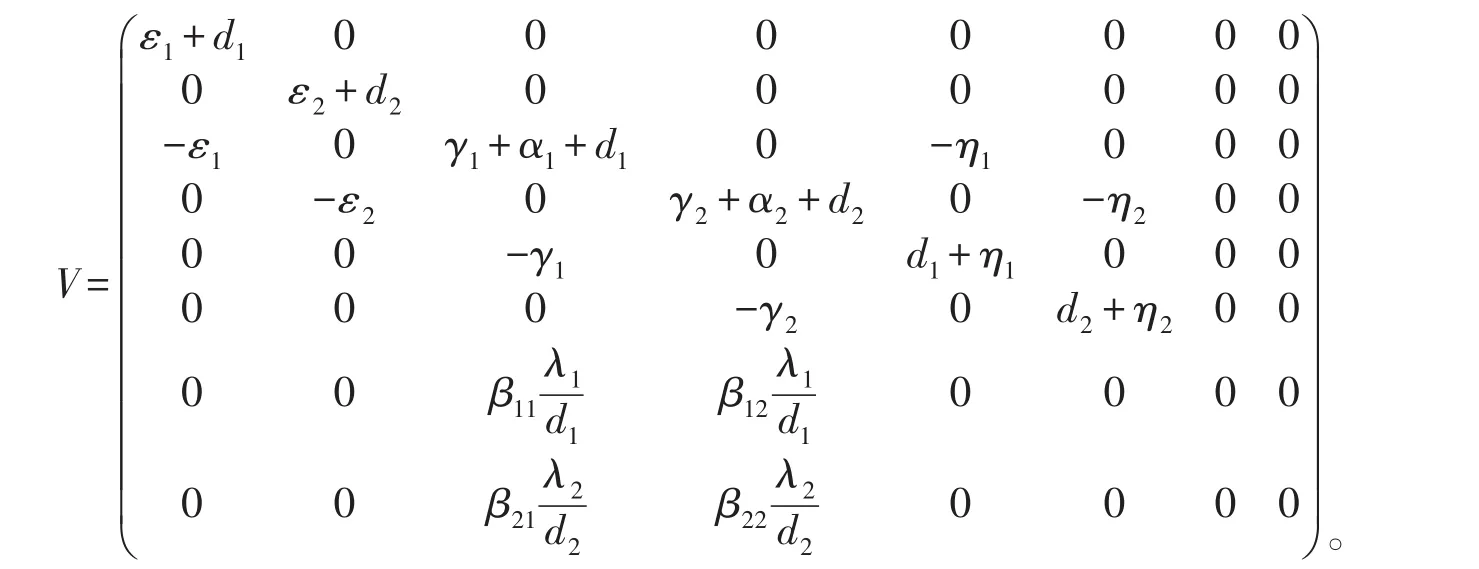
根据矩阵求逆公式求矩阵V-1得：

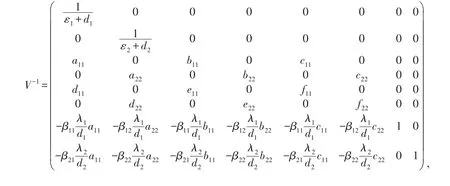
2 稳定性分析

定理如果R0≤1，系统(1)在无病平衡点P0处是全局渐近稳定的；如果R0＞1，系统(1)在无病平衡点P0处是不稳定的。

证明设将系统（1）写成下面的形式：

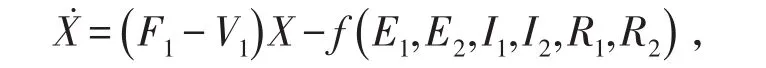
其中F1为F的六阶顺序主子式，V1为V的六阶顺序主子式，且

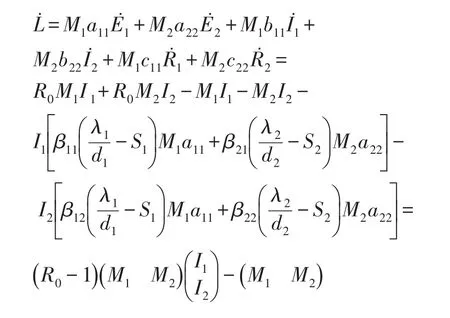
[1]LIU S，WANG S，WANG L.Global dynamics of delay epidemic models with nonlinear incidence rate and relapse[J].Nonlinear Anal Real World Appl.2013，14：1693-1704．

[2]刘力华，冯晓梅.一类带有复发的SEIR模型的全局稳定性[J].运城学院学报，2014，(32)：29-38．

[3]FENG X M，TENG Z D，ZHANG F Q.Global dynamics of a general class of multi-group epidemic models with latency and relapse[J].Math Biosci Eng 2015，12(1)：99-115．

[4]马知恩，周义仓，王稳地，等.传染病动力学的数学建模与研究[M].北京：科学出版社，2004．

[5]王朝瑞.图论[M].北京：北京理工大学出版社，1997．

Global Stability of Two-group Epidemic Models with Latency

FENG Xiao-mei1,WANG Cui-hua1,LU Yong-hong2
(1.Department of Applied Mathematics,Yuncheng University,Yuncheng Shanxi,044000;2.School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009)

In this paper，a two-group model is proposed to describe infectious diseases with latency．By theretical analysis of the model，our results show that the disease free equilibrium of the model is globally asymptotically stable if R0≤1．

basic reproductive number;lyapunov function;global stability

O142

A

1674-0874(2016)01-0001-02

2015-10-16

国家自然科学基金项目[11501498]

冯晓梅（1982-），女，山西运城人，博士，研究方向：种群动力学与传染病动力学。

〔责任编辑 高海〕