SnnSm(n=1～9)团簇结构稳定性与磁学性质的理论研究

孙　林, 王怀谦,2, 吴　梦, 李慧芳, 李孝义, 杜　丹, 沙　蕊

(1. 华侨大学工学院, 泉州 362021; 2. 北京计算科学研究中心, 北京 100094;3. 北京北汽模塑科技有限公司, 北京 102606)



SnnSm(n=1～9)团簇结构稳定性与磁学性质的理论研究

孙林1, 王怀谦1,2, 吴梦3, 李慧芳1, 李孝义1, 杜丹1, 沙蕊1

(1. 华侨大学工学院, 泉州 362021; 2. 北京计算科学研究中心, 北京 100094;3. 北京北汽模塑科技有限公司, 北京 102606)

采用Saunders全局优化随机踢球模型与密度泛函理论相结合的方法, 在B3LYP/SDD理论水平下研究了锡基原子团簇Snn(n=2～10)及锡基稀土原子钐掺杂团簇SnnSm(n=1～9)的几何结构、 稳定性、 电子性质和磁性. 结果表明, 团簇SnnSm(n=1～9)中掺杂的钐原子通常位于主团簇的表面, 掺杂团簇的基态结构更倾向于具有较高对称性的三维结构; 二元锡基混合团簇的平均结合能变大, 稳定性增强, 这主要归因于Sn—Sm键比Sn—Sn键的键能大, 具有更强的相互作用; 掺杂团簇具有较高的磁性, 其总磁矩主要源自于钐原子4f电子的贡献; 随着团簇尺寸的增加, 二元团簇的总磁矩呈现出趋于饱和的现象.

原子团簇; 密度泛函理论; 磁矩; 踢球模型

稀土元素因其独特的电、 光、 磁及热等性能被视为新材料的“宝库”, 其研究受到广泛关注. 稀土元素由于具有独特的4f电子层结构, 其与一些3d元素化合物形成的晶体结构中会形成单轴各向异性, 具有非常优异的超常磁性; 同时由于其独特的电子层结构, 使得其与主族元素和过渡金属元素掺杂不同, 在掺入ⅣA族元素的团簇中时, 会生成一些与主团簇不同的新奇结构, 同时还能提高掺杂团簇的稳定性. 稀土元素Sm作为镧系元素, 具有易被磁化却难被退磁的特性, 是一种潜在的磁性材料原料, 但是关于其掺杂特性的研究报道不多. James等[17]研究了Sm掺杂二氧化铈材料的离子电导率. Fang等[18]采用密度泛函理论研究了纯Sm和Al掺杂Sm团簇的几何结构、 稳定性及电子性质, 发现Sm的掺杂对Al团簇影响较大, 其中Sm原子掺杂是对Al液态系统中短程有序(SRO)的主要因素. Negrier等[19]对Co5Sm团簇进行了研究, 发现与纯Co团簇相比, Co5Sm团簇具有略有增加的各向异性磁性.

目前对钐原子作为杂质原子与金属团簇相互作用的研究较少, 其中有关其与锡基掺杂的二元团簇的研究尚未见报道. 本文采用密度泛函理论, 在B3LYP/SDD理论水平下研究了二元混合合金团簇SnnSm(n=1～9)的几何结构、 稳定性、 电子性质和磁性.

1　计算方法

在密度泛函理论的框架下, 团簇的结构、 能量和电子性质的计算结果与泛函和基组的选择有很大的关系. 为了验证计算方法的可靠性, 首先对纯锡基团簇进行了计算, 得到团簇的平均结合能, 并与实验结果对比; 然后利用纯锡团簇的计算方法对掺杂团簇进行结构及性质的计算. 本文的计算均采用Gaussian 09程序包[20]完成. 本课题组[21～25]采用Saunders的随机踢球[26]结合密度泛函理论的方法完成了小团簇基态结构的预测, 并对所得到的团簇基态结构和电子性质进行了相关分析. 为验证计算方法的可行性, 对纯锡Snn(n=2～10)团簇进行了计算, 其计算过程分为3步: (1) 采用随机踢球的基本模型在各种尺寸下将所有构成团簇的原子放进一个半径可调且足够大的球腔中进行随机组合; 为减少不必要的计算, 对纯锡团簇采用赝势基组Lan2DZ, 在B3LYP/Lan2DZ[27]理论水平下对锡原子数<6的情况进行不少于300次的随机搜寻, 对锡原子数>6的情况进行不少于500次的随机搜寻, 直到没有新的最小能量结构出现为止, 并根据它们的总能量大小对这些异构体进行自动排序; (2) 对所得能量较低的10～30个异构体采用包含相对论效应的Stuttgart-Dresden赝势基组(SDD), 在B3LYP/SDD理论水平下进一步优化, 同时伴随着频率分析; (3) 为了分析在B3LYP/SDD理论水平下的计算精度和对团簇结构优化的合理性, 对得到的基态结构采用高精度CCSD(T)/cc-pVTZ-PP计算方法[28,29]计算其单点能和平均结合能, 并与实验值相比较. 纯锡团簇基态结构见图1, 平均结合能列于表1.

Fig.1　　　　Structure, symmetry point group and electronic state of the Snn(n=2—10) cluster, using B3LYP/SDD calculations

StructureEb/eVB3LYP/SDDCCSD(T)/cc-pVTZ-PPExpt.[30]StructureEb/eVB3LYP/SDDCCSD(T)/cc-pVTZ-PPExpt.[30]Sn20.881.070.94Sn72.092.482.37Sn31.411.501.65Sn82.04Sn41.801.981.94Sn92.08Sn51.882.152.11Sn102.15Sn61.992.342.28

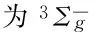
Fig.2　　　　Structure, symmetry point group, electronic state and relative energy(eV) of the lower-lying isomers SnnSm(n=1—9) cluster

2　结果与讨论

2.1几何结构

采用随机踢球结合密度泛函理论的方法, 在B3LYP/SDD理论水平下计算得到SnnSm(n=1～9)团簇的基态结构和低能异构体结构, 如图2所示. 图2给出了它们的电子态、 点群对称和低能异构体的相对能(括号内数值表示高水平CCSD(T)/SDD下计算得到的相对能); 图中所列的结构依据总能量由低到高的顺序进行排序, 在分子式后面用i, ii, iii, iv表示. 在CCSD(T)高水平下, 基态结构没有发生变化, 然而其它较低能异构体有时会出现能级反转的现象.

在B3LYP/SDD理论水平下, 对于双原子团簇SnSm, 其基态结构为SnSm-i, 电子态为5Σg的C∞v直线型结构, Sn—Sm键的键长为0.323 nm, 键能为2.08 eV. 对于三原子团簇Sn2Sm, 其基态结构为Sn2Sm-i所示的二重态Cs的结构, 由1个钐原子连接2个锡原子共同构成平面三角形结构. 对于具有相似平面三角形的异构体Sn2Sm-ii, 其点群对称为C2v, 但其总能量比基态结构Sn2Sm-i高了0.51 eV. 二重态的C2v结构中两个Sn—Sm键的键长完全相等, 但比Cs结构中Sn—Sm键最长的键长长0.007 nm, 故能量较高. 纯锡的三原子团簇的基态结构为倒“V”型, 由于Sn—Sm键的键长大于Sn—Sn键的键长, 导致掺杂团簇为平面三角形结构.

四原子团簇Sn3Sm的基态结构如Sn3Sm-i所示. 由3个锡原子构成等边三角后再与钐原子连接形成“筝形”, 点群对称为Cs, 电子态为7A″. 该结构可看成在纯锡Sn3团簇基态结构的基础上添加1个钐原子构成, 亦可看成1个钐原子替换Sn4团簇基态结构中处于菱形锐角处的1个锡原子构成; 另外, 图2还列出两种Sn3Sm团簇的低能异构体Sn3Sm-ii和Sn3Sm-iii, 它们的能量分别比基态结构高0.71和0.96 eV, 呈现为扭曲的四边形结构, 其中异构体Sn3Sm-ii呈现为三维结构, 它们都具有较低的对称性. 可见, 对Sn3Sm团簇而言, 由于Sn—Sm键长比Sn—Sn键长长0.038 nm, 导致其对称性比锡Sn4团簇的对称性有所降低.

与Sn5结构不同, Sn4Sm的基态结构Sn4Sm-i是一个具有Cs对称由四边形构成的三维多面体结构, 4个锡原子构成向下弯曲的四边形, 而钐原子处于四边形上方, 连接四边形中距离最近的2个锡原子; 异构体Sn4Sm-ii比基态结构能量高0.04 eV, 为C2v点群对称, 同样由4个锡原子构成四边形结构, 但弯曲面朝上, 钐原子处于弯曲面上方, 分别与各锡原子相连接构成三维多面体结构. 异构体Sn4Sm-ii的构成方式与基态结构Sn4Sm-i相似, 均可看作在Sn4团簇基态结构的基础上掺入1个钐原子构成. 异构体Sn4Sm-iii的点群对称为C2v, 但其构成方式与前2种低能结构不同, 呈现为“风筝形”二维平面结构. 由1个钐原子和3个锡原子共同构成平面四边形结构, 钐原子处于四边形的锐角位置, 同时钐原子通过Sm—Sn键键接外部的1个锡原子, 异构体Sn4Sm-iii比基态结构的能量高1.25 eV.

对于六原子团簇Sn5Sm, 其基态结构Sn5Sm-i与Sn6团簇具有相似性. Sn6团簇呈“篮子形”结构, Sn5Sm的基态结构为“皇冠形”结构. Sn5Sm的基态结构Sn5Sm-i可看作是在Sn4Sm基态结构的外围加入1个锡原子得到, 也可看作是通过替换锡Sn6团簇基态“篮子”结构的“篮把”处的锡原子得到, 其点群对称为Cs, 与锡Sn6团簇点群对称C2v相比, 对称性有所降低. 此外, 图2还给出了3种Sn5Sm团簇的低能异构体Sn5Sm-ii, Sn5Sm-iii和Sn5Sm-iv, 其中异构体Sn5Sm-ii所示结构没有任何对称性, 另外两种点群对称均为Cs; 能量分别比基态结构高0.49, 0.98和2.02 eV.

七原子团簇Sn6Sm的基态结构如Sn6Sm-i所示, 可看作是1个钐原子替代Sn7团簇基态结构五角双锥体的一个顶点处的锡原子得到, 也可看作是在Sn6团簇基态结构中掺入1个钐原子得到. 基态结构Sn6Sm-i的点群对称为C2v, 与Sn7团簇的基态结构相比略有畸变. 同原子数锡基掺杂团簇Sn6Pb也具有类似的五角双锥形结构, 具有较高的对称性[16]. 对Sn7团簇的基态结构用钐原子替换掉双锥锥顶的1个锡原子可得到不具有任何对称性的异构体Sn6Sm-ii, 总能量比基态结构高0.38 eV. 图2还列出了另外2种掺钐低能异构体Sn6Sm-iii和Sn6Sm-iv, 能量分别比基态结构高0.62和0.81 eV. 异构体Sn6Sm-iii的点群对称为Cs, 结构呈现为不规则的多面体结构; 异构体Sn6Sm-iv为不具有任何对称性的多面体结构. 从图2可见, 在锡基掺钐团簇中锡原子倾向于构成空间四边形结构, 而钐原子则倾向于跨接在锡原子所构成的空间四边形较长边之上.

Sn7Sm的基态结构Sn7Sm-i可看作是在Sn7团簇的五角双锥形的表面掺入1个钐原子构成, 其点群对称为Cs,相比Sn7团簇的基态结构对称性有所降低. 与Sn8团簇的基态结构相比, 钐原子替换了锥面之上的锡原子后团簇的结构发生了畸变, 钐原子分别与表面的3个锡原子相连. 团簇Sn7Sm的低能异构体Sn7Sm-ii中也存在五角双锥形结构, 但钐原子位于双锥锥顶, 另外1个锡原子在双锥面的边缘单独构成1个面. 异构体Sn7Sm-ii的总能量比基态结构高0.1 eV, 两者能量相近, 具有相同的对称性. 图2还列出了Sn7Sm团簇的两种低能异构体, 异构体Sn7Sm-iii无任何对称性, 异构体Sn7Sm-iv点群对称为Cs, 均呈现为复杂的多面体结构, 它们的总能量分别比基态结构高0.29和0.47 eV.

Sn8Sm的基态结构Sn8Sm-i与Sn8和Sn9团簇的基态结构存在着较大的差异. Sn8Sm的基态结构具有Cs对称, 前方由3个锡原子和1个钐原子共同构成一个向后弯折的四边形结构, 后方由4个锡原子构成矩形, 剩下1个锡原子处于矩形的中心位置, 前方和后方连接起来共同构成“龟壳”结构. 前方四边形中处于锐角位置的钐原子和锡原子构成“龟壳”的“出口”. 图2还列出Sn8Sm团簇的3种低能异构体Sn8Sm-ii, Sn8Sm-iii和Sn8Sm-iv, 三者呈现为复杂的三维多面体结构, 它们无任何对称性, 能量分别比基态结构高0.05, 0.09和0.14 eV.

在Sn8Sm的基态结构Sn8Sm-i中加入1个锡原子, 通过优化可得到团簇Sn9Sm的基态结构Sn9Sm-i, 它是一个具有C2v对称的带有“尾巴”的“灯罩形”三维结构, 可看作是在锡Sn9团簇的基态结构的上方掺入1个钐原子得到的. 与Sn10团簇相比, 结构Sn9Sm-i与其完全不同. 图2还列出了3种异构体Sn9Sm-ii, Sn9Sm-iii和Sn9Sm-iv, 它们的空间结构呈现为复杂的多面体结构, 其中异构体Sn9Sm-ⅲ与基态结构Sn9Sm-i相似, 但其点群对称为C2, 总能量也比基态结构高0.35 eV. 异构体Sn9Sm-ii和Sn9Sm-iv为复杂的多面体结构, 它们不具有任何对称性, 总能量分别比基态结构高0.16和0.39 eV.

总之, 对于钐掺杂锡基团簇的基态结构SnnSm(n=1～9), 可以看作是用1个钐原子替代Snn+1团簇的1个锡原子得到, 或是在带有畸变的稳定团簇Snn中加入1个钐原子得到, 也或是在Snn-1Sm团簇的基态结构中加入1个锡原子得到SnnSm的结构. 从计算得到的钐掺杂锡基团簇的基态结构可见, 钐原子总是占据锡基团簇的表面位置. 在本文的计算中并未发现掺杂的钐原子位于主团簇内部的内嵌式结构, 这与Barman等[16]对锡基铅掺杂团簇的研究结果类似.

2.2平均结合能和二阶差分能

在B3LYP/SDD理论水平下得到Sn—Sn键的键能为1.76 eV, Sn—Sm键的键能为2.08 eV. Sn—Sm键的键能比Sn—Sn键的高0.32 eV, 可推测锡基掺钐团簇比纯锡团簇更加稳定. 为了比较掺杂团簇与纯锡团簇的稳定性, 图3给出了团簇SnnSm(n=1～9)和Snn+1团簇基态结构的平均结合能随团簇尺寸的变化规律. 团簇的平均结合能的计算如下:

(1)

(2)

式中: E(Snn)和E(SnnSm)为基态结构下相应团簇的单点能; E(Sm)和E(Sn)为基态下原子的单点能, 为了比较掺杂前后平均结合能的变化, 给出了两者差值ΔEb的计算公式:

(3)

Fig.3　Average binding energy for the ground-state structures of SnnSm(a) and Snn+1(b) clusters and ΔEb(c)

从图3可见, 随着团簇尺寸的增加, SnnSm(n=1～9)基态结构的平均结合能呈单调递增而未达到宏观块状材料结合能的饱和状态. 从增长趋势来看, 锡基掺钐团簇SnnSm在增长过程中的增长速度明显快于Snn团簇的增长速度; Snn团簇与锡基掺钐团簇SnnSm的平均结合能变化趋势在原子数相同的地方具有相似性, 两者的变化曲线都出现了增速放缓的现象, 如锡原子数为4和7, 其中Sn8团簇更是出现“下折”现象. 在锡基团簇中掺入钐原子后, 团簇的平均结合能明显变大. 掺杂后与掺杂前平均结合能差值ΔEb随着体系尺寸的增大也呈现出增加的趋势, 并且ΔEb均为正值, 表明掺杂后团簇的稳定性得到了提高, 这与通过键能的推测相吻合.

为了衡量掺杂团簇的相对于临近团簇的相对稳定性随团簇尺寸的变化趋势, 计算了团簇SnnSm(n=2～8)的二阶差分能, 作为对照同样计算了锡Snn+1(n=2～8)的二阶差分能. 二阶差分能的计算公式如下:

(4)

(5)

式中: E(Snn)和E(SnnSm)分别为锡团簇和锡基掺钐团簇基态结构下的单点能. 二阶差分能曲线如图4所示.

Fig.4　Second order difference energy of SnnSm(a) and Snn+1(b) clusters

从图4可见, Snn团簇和SnnSm团簇基态结构的二阶差分能均出现一定的奇偶分布的现象. 对Snn团簇而言, 曲线出现了2个峰值, 分别位于Sn4和Sn7, 可见, Sn4和Sn7团簇具有较高的稳定性; 其中Sn7处为最大值, 可知Sn7具有更高的相对稳定性, 这与Assadollahzadeh等[31]的研究结果相符. 而锡Snn团簇的平均结合能增速放缓点Sn5和Sn8则对应于2个谷值处, 说明它们的相对稳定性较差. 在锡基掺杂团簇SnnSm的二阶差分能曲线中同样具有2个峰值, 分别出现在Sn3Sm和Sn6Sm处, 最大峰值出现在Sn6Sm处, 可推知团簇Sn6Sm为掺杂团簇中稳定性相对较高的结构. 掺杂前后体系的二阶差分能呈现出基本一致的变化趋势.

2.3HOMO-LUMO能隙

最高占据轨道(HOMO)和最低空轨道(LUMO)之间的能隙是反映团簇化学活性的重要参数之一, 能隙的大小直接反映了电子从占据轨道向未占据轨道发生跃迁的能力, 从而在一定程度上代表了团簇参与化学反应的能力. 通常, 一个体系的HOMO-LUMO能隙越大, 体系中电子发生跃迁就越难, 则该体系的反应活性越差. 对于小团簇, HOMO-LUMO能隙越大, 相应的团簇化学稳定性越高. 计算了团簇SnnSm(n=1～9)的HOMO和LUMO之间的能隙, 其曲线随原子数目的变化如图5所示.

Fig.5　HOMO-LUMO energy gap of the ground-state structures of SnnSm clusters

从图5可见, 对于锡原子数介于1～7时的掺杂团簇, HOMO-LUMO能隙表现出了明显奇偶交替现象, 具有奇数个锡原子的掺杂团簇的化学活性要弱于与之邻近的团簇. 当锡原子个数n≥7时, 受锡基自身结构影响, 含有偶数个锡原子团簇的能隙要大于含有奇数个锡原子团簇的能隙. 此外, 当锡原子个数为3, 5, 8时出现局域峰值, 其HOMO-LUMO能隙值分别为2.07, 2.19和1.93 eV, 比与之临近的团簇的能隙要高, 可以推测它们的化学活性更低. Sn7Sm团簇具有最低的能隙(1.53 eV), 表明其化学活性较强, 化学稳定性最差, 这与二阶差分能的分析结果一致.

2.4磁性

根据Hund规则, 由于稀土金属元素具有未填满电子的d轨道和f轨道, 因而孤立的团簇将会具有磁性. 对团簇磁矩进行理论研究可以获得与磁矩相互依赖的团簇结构性质, 从而可以理解团簇的尺寸、 几何和电子结构与磁性的关系, 而通过实验很难对其进行判定. 团簇的总磁矩与团簇的结构、 自旋多重度和电子的轨道有关, 但钐元素作为镧系元素受轨道角动量猝灭影响, 自旋磁矩做贡献, 而轨道角动量不做贡献, 所以仅分析自旋磁矩. 团簇的自旋多重度为(2S+1)与总磁矩M(μB)的关系为M=2S. 团簇总磁矩如图6所示.

由图6可知, 锡基掺钐团簇的总磁矩先随团簇尺寸的增加而增加, 后稳定在6μB处趋于饱和状态. 为了进一步理解团簇SnnSm(n=1～9)的磁性, 采用自然布局分析(NPA)法计算了掺杂团簇中各个原子的局域磁矩. 得到的局域磁矩如图7所示, 其中重点分析了钐原子6s, 4f和5d电子层对总磁矩的贡献. 图7中Sm-6s, Sm-4f和Sm-5d分别代表钐原子6s, 4f和5d层电子对磁矩的贡献. 同时为了便于比较, 图中也给出了团簇中各类原子的总磁矩贡献. 其中, Sn-M和Sm-M分别表示团簇中所有Sn原子对总磁矩的贡献和Sm原子对总磁矩的贡献.

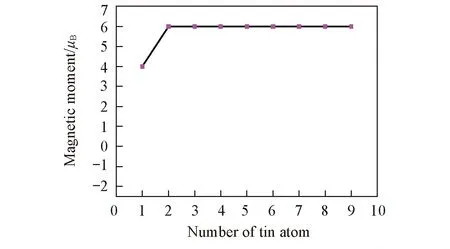
Fig.6　　　　Total magnetic moments of SnnSm clusters

Fig.7　Magnetic moments contribution of 6s,4f and 5d states for Sm atom in SnnSm clusters and local magnetic moments of the Sn and Sm atom

从图7可见, 团簇的总磁矩贡献主要来源于钐原子. 在双原子掺杂团簇中, 锡原子的局域磁矩表现为抗磁矩, 对总磁矩的贡献为负值; 在多原子掺杂团簇中锡原子的局域磁矩较小, 对总磁矩的贡献可以忽略不计. 掺杂团簇中钐原子的局域磁矩主要集中在4f电子轨道, 而6s和5d轨道对它的局域磁矩的贡献很小, 也基本可以忽略. 说明团簇SnnSm(n=1～9)的磁性主要来源于钐原子的4f电子轨道.

表2给出了SnnSm(n=1～9)团簇中Sm原子的价电子组态, 可见, Sm原子6s电子轨道电子发生了转移. Sm原子基态下价电子组态为4f66s2, 由于Sm(1.17)原子的电负性比Sn(1.96)原子的小, 在与Sn原子混合形成团簇后产生了更强的杂化耦合作用, 导致了Sm中6s轨道的电子向Sn原子5p轨道发生了部分转移, 从而使混合团簇更加稳定. 此外, Sm原子内部6s轨道的电子向能量更高的态也发生了部分的转移, 并且随着团簇尺寸的增加, 能量更高态的电子占据数呈现出增加的趋势. 需要说明的是, Sm原子自身4f轨道的电子占据数并没有发生实质的变化, 这也是混合团簇SnnSm(n=1～9)保持较高磁性且随着团簇尺寸增加其总磁矩呈现出趋于饱和现象的本质原因.

Table 2　Valence electron configuration of Sm atom in the SnnSm(n=1—9) cluster

3　结　　论

采用Saunders全局优化随机踢球与密度泛函理论相结合的方法, 研究了锡基掺钐的小团簇SnnSm(n=1～9)基态结构下的平均结合能、 二阶差分能、 HOMO-LUMO能隙及团簇的磁性随着团簇尺寸增加的变化关系. 结果表明, 锡基掺钐团簇的增大遵循一定的结构模式, 即掺杂钐原子总是占据着锡基团簇表面位置的外嵌式基态结构. 而掺杂团簇的基态结构可由钐原子在锡团簇的基态结构中替换表面的一个锡原子或在畸变的锡基团簇的表面直接掺入而获得. 通过对掺杂团簇与纯锡团簇平均结合能和二阶差分能的比较发现, 掺杂团簇的平均结合能明显大于纯锡团簇的平均结合能, 而且二者的差值随着掺入体系的增加而增加, 说明锡基掺钐团簇的稳定性要高于纯锡团簇; 掺杂前后体系的二阶差分能呈现出一致的变化趋势. 掺杂团簇HOMO-LUMO能隙在锡原子数介于1～7之间时表现出了明显的奇偶交替现象, 具有奇数个锡原子掺杂团簇的化学活性要弱于与之邻近的团簇; 当锡原子个数n≥7时, 受锡基自身结构影响, 偶数个锡原子团簇的能隙要比奇数个锡原子团簇的大. 随着团簇尺寸的增加, 二元团簇的总磁矩呈现出趋于饱和的现象; 在双原子团簇中, 锡原子的局域磁矩表现为抗磁矩, 在多原子团簇中锡原子的局域磁矩很小, 对总磁矩的贡献可忽略不计, 掺杂团簇的磁矩主要来源于钐原子4f电子的贡献.

[ 1 ]Jing Q., Ge G. X., Cao H. B., Huang X. C., Liu X. Y., Yang H. X.,ActaPhys. -Chim.Sinia, 2010, 26(9), 2510—2514(井群, 葛桂贤, 曹海宾, 黄旭初, 刘效勇, 闫红霞. 物理化学学报, 2010, 26(9), 2510—2514)

[ 2 ]Chen L., Xu C., Zhang X. F.,ActaPhys.Sinica, 2009, 58(3), 1603—1607(陈亮, 徐灿, 张小芳. 物理学报, 2009, 58(3), 1603—1607)

[ 3 ]Lu Z. H., Cao J. X.,Chin.Phys.B, 2008, 17(9), 3336—3342

[ 4 ]Zhang C. R., Chen Y. H., Wang D. B., Wu Y. Z., Chen H. S.,Chin.Phys.B, 2008, 17(8), 2938—2950

[ 5 ]Baletto F., Ferrando R.,Rev.Mod.Phys., 2005, 77(1), 371—423

[ 6 ]Jones R. O.,J.Chem.Phys., 1999, 110(11), 5189—5200

[ 7 ]Handschuh H., Gantefor G., Kessler B., Bechthold P. S., Eberhardt W.,Phys.Rev.Lett., 1995, 74(7), 1095—1098

[ 8 ]Yoo S., Zeng X. C.,J.Chem.Phys., 2006, 124(5), 054304

[ 9 ]Qin W., Lu W. C., Zhao L. Z., Zang Q. J., Chen G. J., Wang C. Z., Ho K. M.,J.Chem.Phys., 2009, 131(12), 124507

[10]Li X. P., Lu W. C., Zang Q. J., Chen G. J., Wang C. Z., Ho K. M.,J.Phys.Chem.A, 2009, 113, 6217—6221

[11]Zhu X. L., Zeng X. C., Lei Y. A., Pan B. C.,J.Chem.Phys., 2004, 120(19), 8985—8995

[12]Zhao L. Z., Lu W. C., Qin W., Zang Q. J., Wang C. Z., Ho K. M.,J.Phys.Chem.A, 2008, 112(26), 5815—5823

[13]Drebov N., Oger E., Rapps T., Kelting R., Schooss D., Weis P., Kappes M. M., Ahlrichs R.,J.Chem.Phys., 2010, 133(22), 224302

[14]Zang Q. J., Chen G. J., Qin W., Zhao L. Z., Lu W. C.,Chem.Res.ChineseUniversities, 2013, 29(3), 579—583

[15]Clayborne P. A., Gupta U., Reber A. C., Melko J. J., Khanna S. N., Castleman A. W. Jr,J.Chem.Phys., 2010, 133(13), 134302

[16]Barman S., Rajesh C., Das G. P., Majumder C.,Eur.Phys.J.D, 2009, 55, 613—625

[17]James H., Arif I., Giorgi J. B., Tom K. W.,Phys.Chem.Chem.Phys., 2010, 12, 12969—12972

[18]Fang X. W., Wang C. Z., Yao Y. X., Ding Z. J., Hupalo M., Tringides M. C., Ho K. M.,Phys.Rev.B, 2011, 83(22), 224203

[19]Negrier M., Tuaillon-Combes J., Dupuits V., Perez A., Pellarin M., Broyer M.,Eur.Phys.J.D, 1999, 9, 475—478

[20]Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Mennucci B., Petersson G. A., Nakatsuji H., Caricato M., Li X., Hratchian H. P., Izmaylov A. F., Bloino J., Zheng G., Sonnenberg J. L., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Montgomery J. A. Jr., Peralta J. E., Ogliaor F., Bearpark M., Heyd J. J., Brothers E., Kudin K. N., Staroverov V. N., Keith T., Kobayashi R., Normand J., Raghavachari K., Rendell A., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Rega N., Millam J. M., Klene M., Knox J. E., Cross J. B., Bakken V., Adamo C., Jaramillo J., Gomperts R., Stratmann R. E., Yazyev O., Austin A. J., Cammi R., Pomelli C., Ochterski J. W., Martin R. L., Morokuma K., Zakrzewski V. G., Voth G. A., Salvador P., Dannenberg J. J., Dapprich S., Daniels A. D., Farkas O., Foresman J. B., Ortiz J. V., Cioslowski J., Fox D. J.,Gaussian09,RevisionC.01, Gaussian Inc., Wallingford CT, 2010

[21]Wang H. Q., Li H. F., Zheng L. X.,J.Magn.Magn.Mater., 2013, 344, 79—84

[22]Li H. F., Wang H. Q.,Phys.Chem.Chem.Phys., 2014, 16, 244—254

[23]Wang H. Q., Li H. F., Kuang X. Y.,Phys.Chem.Chem.Phys., 2012, 14, 5272—5283

[24]Wang H. Q., Li H. F.,J.Chem.Phys., 2012, 137(16), 164304

[25]Wang H. Q., Li H. F., Wang J. X., Kuang X. Y.,J.Mol.Model., 2012, 18, 2993—3001

[26]Bera P. P., Sattelmeyer K. W., Saunders M., Schaefer III H. F., Schleyer P. R.,J.Phys.Chem.A, 2006, 110(13), 4287—4290

[27]Becke A. D.,J.Chem.Phys., 1993, 98(7), 5648—5652

[28]Bartlett R. J., Musial M.,Rev.Mod.Phys., 2007, 79(1), 291—352

[29]Peterson K. A.,J.Chem.Phys., 2003, 119(21), 11099—11112

[30]Gingerich K. A., Desideri A., Cocke D. L.,J.Chem.Phys., 1975, 62(2), 731—732

[31]Assadollahzadeh B., Schafer S., Schwerdtfeger P.,J.Comput.Chem., 2010, 31(5), 929—937

(Ed.: Y, Z, S)

† Supported by the Program for New Century Excellent Talents in Fujian Province University, China(No.2014FJ-NCET-ZR07), the Program for Excellent Youth Talents in Fujian Province University, China(No.JA13009) and the Natural Science Foundation of Fujian Province, China(No.2014J05006).

Theoretical Studies on the Structure Stability and Magnetic Properties of SnnSm(n=1—9) Clusters†

SUN Lin1, WANG Huaiqian1,2*, WU Meng3, LI Huifang1, LI Xiaoyi1, DU Dan1, SHA Rui1

(1.CollegeofEngineering,HuaqiaoUniversity,Quanzhou362021,China; 2.BeijingComputationalScienceResearchCenter,Beijing100094,China; 3.BeijingBeiqiMould&PlasticTechnologyCo.Ltd.,Beijing102606,China)

The geometrical structures, relative stabilities, electronic properties and magnetism of tin clusters and bimetallic complexes of tin clusters with one samarium atom SnnSm(n=1—9) were investigated with the Saunders “Kick” global stochastic search technique combined with density functional theory(DFT) calculations at the B3LYP/SDD level of theory. The results are as follows: (1) Samarium atom usually located on the surface in the doped tin-based with one samarium atom clusters. And the ground-state structures of the SnnSm(n=1—9) clusters prefer to three-dimensional structure with higher symmetry; (2) after doping samarium atom in the Sn-based cluster, the cluster has the increase average binding energy which should owe to the fact that the bonding energy of Sn—Sm bond is higher than Sn—Sn bond and has the stronger interaction; (3) the doped Sn-based with one samarium atom cluster has large magnetic moments, and the contribution of magnetic moment almost comes from 4felectron orbit of the samarium atom, while the contribution of tin atoms is negligible. With the increase of cluster’s size, bimetallic complexes cluster has the special phenomenon that the total magnetic moment tends to be stable.

Atomic cluster; Density functional theory; Magnetic moment; Kick model

10.7503/cjcu20160318

2016-05-09. 网络出版日期: 2016-09-20.

福建省高校新世纪优秀人才支持计划项目(批准号: 2014FJ-NCET-ZR07)、 福建省高校杰出青年科研人才培育计划项目(批准号: JA13009)和福建省自然科学基金(批准号: 2014J05006)资助.

O641

A

联系人简介: 王怀谦, 男, 博士, 副教授, 主要从事纳米团簇与光电子能谱研究. E-mail: hqwang@hqu.edu.cn