装备故障隔离模糊度要求值的确定和优化方法

吕建伟，谢宗仁，徐一帆

（海军工程大学管理工程系，湖北　武汉 430033）

装备故障隔离模糊度要求值的确定和优化方法

吕建伟，谢宗仁，徐一帆

（海军工程大学管理工程系，湖北武汉 430033）

从故障隔离率的基本定义和分析出发，针对在装备研制早期，给定故障隔离百分比后，对如何确定和优化对应的故障隔离模糊度问题进行了研究。首先，借助于测试性分析中的多信号流图（multi-signal flow graph，MSFG）及其示例计算结果，结合测试性设计中故障模糊度的不同分布，得到了故障隔离模糊度的完整的度量指标（包括最小值、最大值、均值），以及当前指标的物理意义（单个指标应理解为均值）。在定性分析的条件下，通过典型案例分析，给出了最小值、最大值和均值确定的方法和原则。在定量分析方面，通过装备维修和故障隔离过程分析，建立了故障隔离模糊度的通用优化模型。在模型求解方面，对模型进行了工程应用简化，给出了模型优化解存在的前提条件，通过逻辑和数学分析等手段，结合典型示例给出了模型求解的逐步寻优算法和动态规划算法，应用该模型和算法可以在给定故障隔离百分比的条件下，得到经过优化的故障隔离模糊度的最小值、最大值和均值的精确解。从而在工程应用的背景下，较为圆满地解决了这一问题。

研制早期；测试性分析；故障隔离；模糊度；优化模型

网址：www.sys-ele.com

0　引　言

故障隔离率PI定义为在规定的时间内，用规定的方法将检测到的故障正确隔离到不大于规定的可更换单元（line replaceable unit，LRU）数的故障数与同一个时间内检测到的故障数之比。显然，PI的定义涉及到不可分割的两个方面，一个是成功隔离已检测到的故障的比例（百分比），另一个是“正确隔离到不大于规定的可更换单元”的问题。为表达方便起见，这里将前者称为故障隔离百分比，将后者称为故障隔离模糊组，对应的数值L称为模糊度。

目前，对于如何规定故障隔离百分比的要求，目前已经有了较多的研究和对应的成果［17］。但是，人们在规定所必须达到的故障隔离率指标时，如果只规定隔离百分比，不提所对应的模糊度要求，显然只是规定了一个不完整的指标，且存在后期无法验证的问题；如果默认所规定的隔离百分比是单一隔离（隔离到单个可更换单元LRU）的百分比，即L=1，则可能存在隔离要求过高，难于实现的问题，且这样考虑问题可能有些片面和极端化。因为实际上，对于现场修理而言，即使隔离到L=2，甚至L=3时，也是有意义的，这总比没有任何故障隔离能力要强得多。

综上所述，在装备研制的早期阶段，例如可行性论证和方案设计阶段，对于装备的故障隔离率指标而言，如何在规定故障隔离百分比的同时，合理的规定所对应的故障隔离模糊组的大小（模糊度），以便于作为装备研制后续阶段的测试性设计的依据和指导性要求，并以较为合理的设计措施和成本来实现和达到这一指标，目前这个问题实际上尚未解决，仍处于经验和估计状态［8］，有待进一步深化，本文就此问题进行较为系统的研究。

1　故障隔离百分比和隔离模糊组

在装备研制早期，当通过需求和类比分析等方法，确定了装备的故障检测率、故障隔离率数值（百分比）指标［912］要求时，对其中的故障隔离率指标，实际仅仅解决了问题的前一个方面（成功隔离的比例），这里着重探讨问题的后一个方面，即在确定故障隔离率数值（百分比）的同时，如何规定其对应的模糊组的大小（模糊度）L。

显然，如果L=1，就是唯一隔离，这对于现场维修活动而言无疑是很有利的，因为维修人员可以根据故障隔离信息，对LRU进行快速拆卸和更换；如果L＞1，表示在现有测试点的条件下，人们不能根据已有信息进行故障的单一隔离，就形成了一个模糊度为L的模糊组［1317］，这就是模糊隔离，那么维修人员还要通过其他手段进一步分析（例如采用反复拆卸、更换和检查，或采用自动测试系统（automatic test system，ATS）等手段），才能将故障精确定位到某个LRU，尔后对该LRU进行更换。

2　关于L值取值的初步分析

根据以上分析，在现有测试点和测试设置条件下的不可区分的故障状态所包含的单元数量（LRU的数量）即为故障隔离模糊组的大小。分析可知，在给定的装备结构组成和测试点布局的情况下，该值具有以下特点：

（1）L值是一个设备级（故障隔离）的概念，对于不同的设备结构、测试点布局和组成而言，可以出现完全不同的模糊组大小L值。

（2）L值的大小随不同的故障而变，即对于不同的故障，在装备、测试点相同的情况下，可以隔离到不同的模糊组大小L。

（3）L值的大小，还与LRU的划分有关。如果LRU包含较多的SRU或零部件（相应的，整个装备就包含较少的LRU），则L=1较易做到；反之则较难做到。

（4）只要测试（点）足够多，对于任何装备的任何故障都可以做到唯一性隔离。因此规定的必须达到的或要求的L值的大小，本质上是一个成本问题。

根据以上分析，装备故障隔离模糊度L的确定，需要具备以下几个条件：

（1）装备的结构、布局、各部分组成已经确定；

（2）装备在服役以后，可能出现的各类故障模式已经确定；

（3）装备已经开展测试性设计，故障测试方案已经确定，测试（点）布局已知。

同时具备以上几个条件的话，那么装备的研制必然已经到了后期阶段，例如技术设计或详细设计阶段（有时亦称为工程研制阶段）。那么，在装备研制的早期阶段，如何在早期对该值做出合理的规定呢？下面首先介绍，在进行测试性设计和分析时，L指标的确定方法。

3　基于多信号流图模型的装备测试性分析

在装备基本结构设计已经完成，且测试点和整体布局也已经确定的情况下，一般可以通过多信号流图（multi-signal flow graph，MSFG）模型［1822］的相关性矩阵来确定故障隔离模糊组，同时还可以确认目前的测试点设置结果所对应的相关测试性指标，如：故障检测率、故障隔离率（含百分比和模糊组）等。这个分析过程相当于完成了一次较为完整的装备测试性设计和分析步骤。

多信号流图模型的相关性矩阵及其分析过程包括：

（1）定义所分析的装备或系统；

（2）进行（failure mode effects and criticality analysis，FMECA/FMEA）分析，确定故障模式及其影响；

（3）对系统进行结构、功能、原理等分析，得到各部分之间关联和传递的逻辑关系；

（4）根据分析的结果，确定测点的位置并赋予其测试功能，产生多信号流模型；

（5）根据该模型，确定故障和测试的相关性D矩阵；

（6）分析各个故障与测试之间的相关性，识别未检测故障、模糊组和冗余测试。

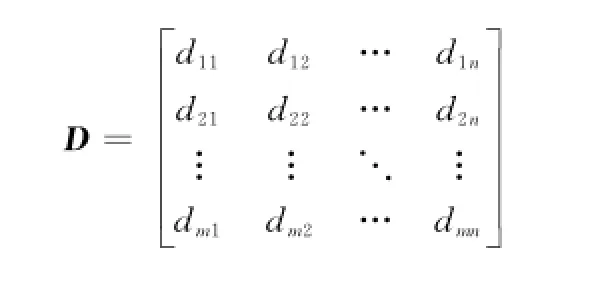
故障-测试相关性D矩阵的形式为式中，n为测试数量；m为故障模式数量；dij表示第j个测试tj与第i个故障状态si的相关性，当第j个测试检测不到第i个故障时，dij=0，否则dij=1。表1为某D矩阵的示例［23］。

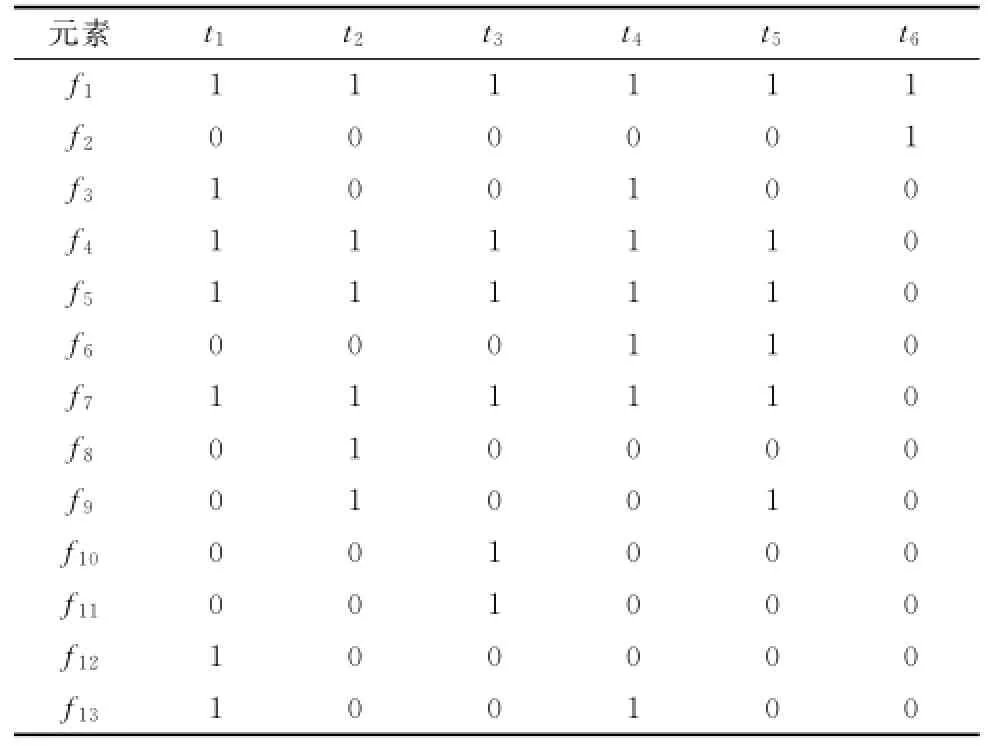
表1　某装备的故障－测试相关性矩阵

限于篇幅，表1中仅包含6个测试，13个故障模式。以下分析各个故障与测试之间的相关性（单故障分析）并计算测试性指标。

（1）识别某行所对应的未检测故障：如果相关性矩阵某行fi=（di1，di2，…，din）中，dij=0（j=1，2，…，n），该行即可表示一个未能检测出的故障。

（2）识别对应的故障隔离模糊组：逐个比对以上D矩阵中的各个行向量，若fi=fj（j≠i），这2行所表示的故障是无法进一步区分的，按照定义，它们构成了一个隔离模糊组，在处理上可将这2行进行合并处理。表1中的隔离模糊组包括：｛f3，f13｝、｛f4，f5，f7｝、｛f10，f11｝，对应的模糊度最大值Lmax=3。合并后的D矩阵如表2所示。

（3）对冗余测试进行判别：对比D矩阵的各个列向量，如果有ti=tj（j≠i），可认定对应的列互为冗余［24］。

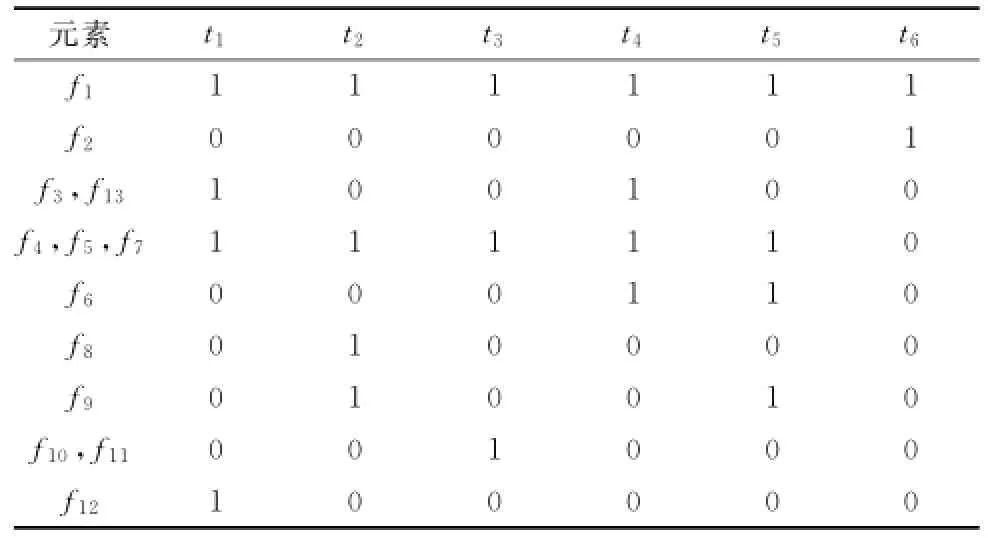
表2　某装备的故障－测试相关性矩阵（简化）

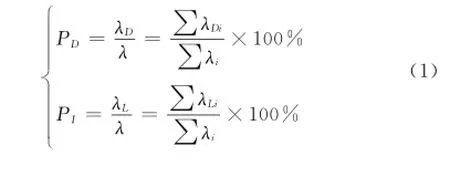
下面计算其对应的测试性指标，计算公式如下：式中，λ为全部故障的故障率之和；λD为全部可检测故障的故障率之和；λi为第i个故障所对应的故障率；λDi为第i个检出故障所对应的故障率。λL为隔离到≤L个LRU的故障所对应的故障率之和，λLi的含义与前类似，L为模糊度。

各组成单元（故障）的平均故障间隔时间（mean time between failure，MTBF）和故障率（×10-3）如表3所示。

表3　各组成单元（故障）的　MTBF和故障率

根据式（1）计算可得：

因为全部故障都能通过现有测试而被检测，因此有PD=100%。

L=1时，f1，f2，f6，f8，f9，f12能被隔离到位，所以有

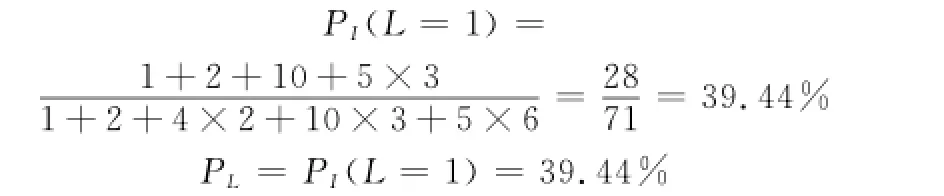
L=2时，增加｛f3，f13｝、｛f10，f11｝能被隔离到位，所以有

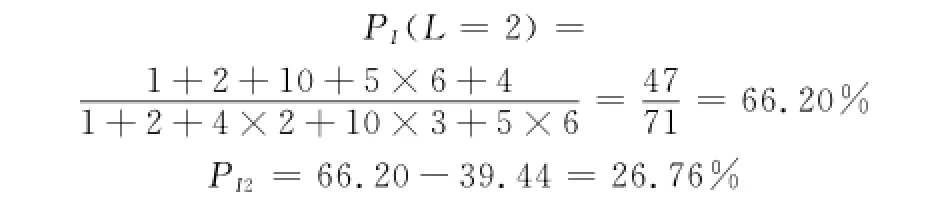
L=3时，所有故障均能被隔离到位，即PI（L=3）= 100%。PI3=100-66.20=33.80%。

以下是根据该例的计算结果，所做的关于故障平均隔离模糊度的某些分析。

（1）在正常的测试性设计条件下，一般都有部分故障被唯一性隔离，即PI（L=1）＞0。

（2）表2中共有13个故障模式，其中只有9个可独立识别，平均隔离模糊度

（3）该示例中，要使得最大隔离模糊度Lmax降低为2，需要至少增加1个测试（点）；要使得Lmax降低为1，需要至少增加4个测试。假设所增加的各测试（点）的成本相等，需分别增加成本17%和67%。

4　定性分析及其处理方法

4.1分布类型分析

从以上计算结果可以推知，如果最大模糊度Lmax≫平均模糊度L¯，且处于Lmax的数量较少，那么使得该测试方案的最大模糊度Lmax降低的成本是较低的；反之，如果最大模糊度Lmax和平均模糊度¯L数值相近，例如Lmax-¯L≤1，且处于Lmax的数量较多，那么使得该测试方案的最大模糊度Lmax降低的成本是较高的。这两种情况分别对应以下两种分布。

（1）偏离型分布

最大模糊度Lmax≫平均模糊度时，Lmax较易降低。例如Lmax-≥1时，只要增加1个测试（点），就能使Lmax降低1，即有L′max=Lmax-1，如图1所示。

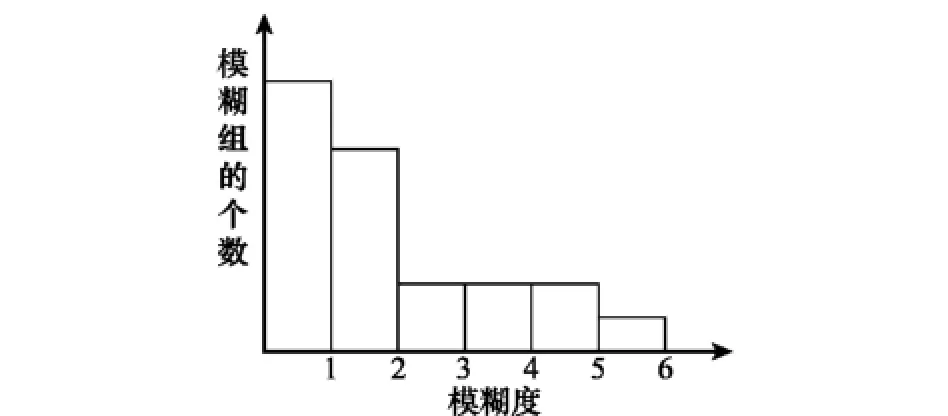
图1　模糊组为偏离型分布的示意图

（2）重叠型分布

最大模糊度Lmax和平均模糊度数值相近，即Lmax-≤1时，不易降低Lmax，如图2所示。

图2　模糊组为重叠型分布的示意图

4.2对于L值（要求值）确定的方式和实现方法的建议

在定性分析时，在设备级别，如果不对故障诊断的成本做特别约定，可以采用类比法，参照现有的取值范围，确定为1～3为宜。其含义为：一个装备，只要是进行了专门的测试性设计，那么有相当一部分（大部分）故障应是可以做到隔离到单个LRU的，否则开展测试性设计就没有意义了，即有Lmin=1；其次，测试性设计的结果，应将部分（或小部分）故障隔离到2个LRU；在极端的情况下，对于个别故障隔离到3个LRU也是允许的，即有Lmax=3。

在这样的规则指导下，一般来说会有L-≈1.5。换句话说，一个具体装备（设备）或系统的允许L值，就不可能仅仅用单个数值来描述，而应当采用3个数值来描述：最大值Lmax、最小值Lmin和平均值L-。且单个数值表示的，实际上其含义应是平均值L-。表4给出一个装备故障隔离模糊度的示例。

表4　装备故障隔离模糊度的示例

在该示例中，Lmax=3，Lmin=1，=1.50。相应的L=1时，PL=0.60；L=2时，P（L=2）=0.90；L=3时，P（L=3）= 1.00。

不同的装备在论证和研制过程中，可能会处于不同的技术成熟度（technical readiness level，TRL）［25］状态。此时，对于这种TRL较低的情况（例如TRL＜6），人们所掌握的定量信息较少，对于其隔离模糊度可以采用本节建议的基于定性分析的方法来规定。反之可以采用下面的定量分析方法进行优化。

5　定量优化模型的建立和分析

分析可知，装备故障修复时间t通常由准备时间t0、故障定位隔离时间t1、拆卸更换时间t2、再安装时间t3和调整和检验时间t4等组成。即有t=t0+t1+t2+t3+t4，如图3所示。

图3　故障排除流程图

而平均故障修复时间（mean time to repair，MTTR）即为故障修复时间t的平均值。其中当没有BIT和自动故障隔离定位能力时（即PI=0）的隔离定位时间（对应以上t1）用tIN表示，其余时间（对应t0，t2，t3和t4）用tO表示。

根据本文上一节的分析，装备的故障隔离率PI实际上是一个复合指标，即L=1（唯一性隔离）时的PL，L=2时的PI2，…，L=n时的PIn（n为组成装备的LRU的数量），且有

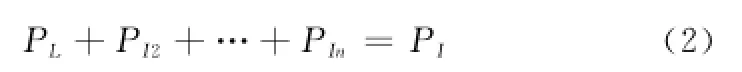
对于PI中的PL成分而言，由于这部分故障做到了唯一性隔离，可以认为其故障隔离时间很短，与人工隔离相比近似认为是0，因此对于上述故障隔离时间tIN的影响是产生了一个-αL×tIN×PL的增量，其中αL=1.0，可定义为PL的隔离组影响因子（isolation group influence factor，IGIF）。

对于PI2，在现场修复条件下可能进行至少1次、至多2次人工换件来隔离故障，在出现共因失效（common cause failure，CCF）时，甚至需要人工3次换件才能完成故障隔离，其计算式为

。和PL相比，对于tIN的有利的增量影响相对较低，即PI2的IGIF指标αI2＜1.0，相应的增量效果为-αI2×tIN×PI2。

同理，对于PI3，不考虑CCF时，为了隔离故障，其现场人工换件次数为至少1次，至多3次；考虑CCF时，为隔离而进行的人工换件次数可能多达7次，其计算式为，其增量效果为-αI3×tIN×PI3，等等，余类推。因此有

在以上分析的基础上，这里给出如下几种优化形式。（1）对于指定的故障隔离百分比要求值，使平均修复时间达到最小。

此即为对式（3）取最小值，由于tO、tIN为定值，所以仅对式（3）的后一部分取极值即可。式（2）为此优化问题的约束条件；各PI的组成部分PIi均有大于0的要求。与此同时，考虑到问题的物理意义，为尽量减少对于产品基本可靠性的不利影响，对于该问题而言，还应当考虑λ≤λ0约束，其中λ=1/MTBF为产品的基本可靠性指标。

以上可归结为

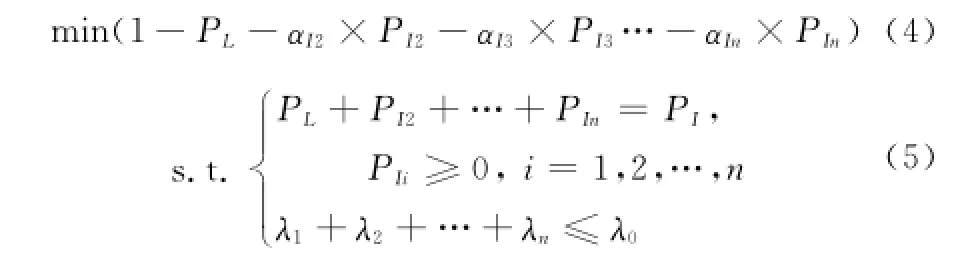
由式（4）的函数特点和式（5）的约束条件可知，该优化问题的最优解为PL=PI，PI2=PI3=…=PIn=0，其对应的物理意义为：在不考虑成本且要求维修效果最好（平均维修时间最短）的情况下，如果能够满足基本可靠性要求，那么做到唯一性故障隔离即为最优解。

（2）对于指定的故障隔离百分比和平均修复时间，使实现指定的故障隔离百分比的成本最低。

在这种条件下，式（3）或式（4）以及式（5）均成为约束条件，所求优化问题的解应满足C（PL）+C（PI2）+…+C（PIn）最小化。考虑到故障隔离的成本由PL、PI2直至PIn，成本渐次降低，即有实现PL的成本C（PL）最高，C（PI2）次之…。在此基础上，可以将其目标函数表示为

式中，αC1，αC2，…，αCn分别为实现PL，PI2，…，PIn的费用系数，这里可将其称为费用影响因子（cost influence factor，CIF）。

因此该优化问题可表示为

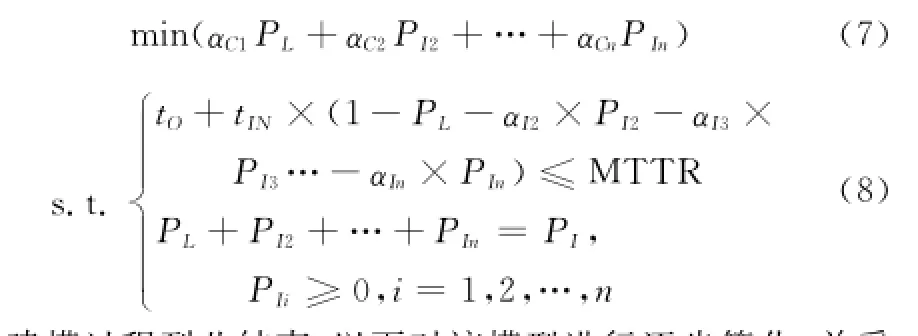
建模过程到此结束，以下对该模型进行逐步简化，并采用典型数据对模型进行求解。

首先，根据故障排除过程和对于式（3）的推导过程可知，在实际工作中，考虑L＞3意义不大，同时也为了计算简便起见，在以下优化计算中不考虑L＞3时的情况，即有PL+PI2+PI3=PI。优化模型变为

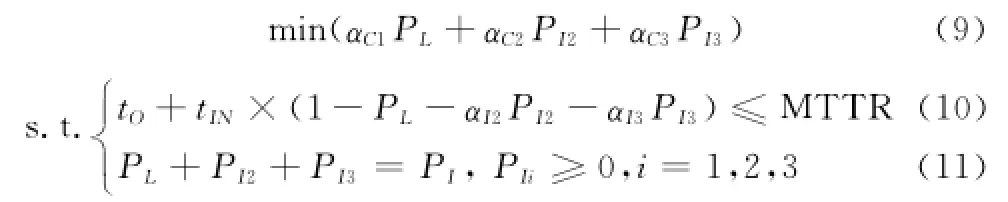
求解该问题的最优解的前提是问题有解，考虑到一般有αC1＞αC2＞αC3且有αL＞αI2＞αI3，可首先令PL=PI，且PI2= PI3=0，校核MTTR约束条件式（10），如果不成立，则问题无解；反之可用下一节所述的方法求解。

6　求解最优解的方法及其分析

分析可知，对于该优化问题可以采用多种方法求解，例如下面给出的逐步寻优算法、动态规划算法，以及线性规划的单纯形法等。以下给出具体算法并结合具体示例进行优化求解。

6.1逐步寻优算法

该算法首先考虑实现PI3、PI2、PL的成本渐次增大（αC3＜ αC2＜αC1），首先将要求的故障隔离率PI全部赋予PI3。然后逐步减小PI3，同时逐步增大PI2；或逐步减小PI2，同时逐步增大PL。直至式（10）成立为止。具体算法如下。

步骤1令PL=PI2=0，PI3=PI，校核式（10），如果成立，结束，否则转入步骤2。

步骤2按某一固定的步长减小PI3，同时增大PI2，校核式（10），如果成立，结束；否则，若PI3＞0，转入步骤2，若PI3=0，转入步骤3。

步骤3按某一固定的步长减小PI2，同时增大PL，校核式（10），如果成立，结束。否则，若PI2＞0，重新执行步骤3；若PI2=0，该问题无解。

以下对某装备的一组具体数据，采用上述算法进行求解。

某装备原有维修性指标MTTR为3 h，其中tO=0.9 h，tIN=2.1 h。现考虑对其进行专门的测试性设计，指标要求值为PI=0.90，MTTR目标值为2 h。试确定其优化结果。

根据以上数据和装备的背景信息，分别对于式（10）中IGIF的αI2和αI3进行近似处理。根据对该装备所进行的FMECA分析的结果，考虑αI2的物理意义（PI2所对应的tIN减少的有利效果的百分比），和αL的取值相比，这里将其取为1/2，考虑到该装备的实际LRU组成可知，这样的取值是有些偏于悲观且对优化结果是有利的。类似的，可取αI3=1/4。

取定了这些参数后，代入以上模型并采用Matlab编程进行求解，优化结果为（0.052 4，0.847 6，0），对应的¯L= 1.747 6。

下面计算其费用指标。对于式（9）中CIF的各个组成部分αC1、αC2、αC3，对于该装备而言，可以假设实现相同的故障隔离效果（故障隔离时间的减小）的成本相同或相当，参照前述IGIF的处理方式，可令αC3=1。类似地，有αC2=2，且有αC1=4。按此计算可得费用指标C=1.904 8。

6.2动态规划方法

首先将以上通过分析得到的参数分别代入式（9）和式（10）可得如下优化模型：

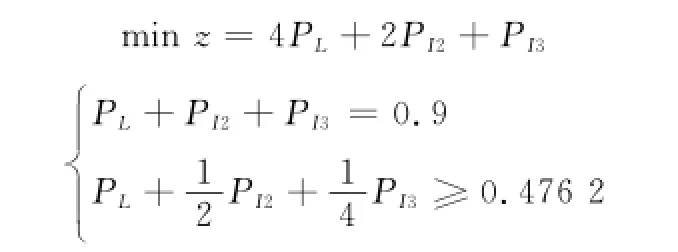
对于该模型，可用动态规划的逆序法进行求解。根据决策变量将求解过程划分为3个阶段。

决策变量为：PL，PI2，PI3，状态变量为s1，s2，s3，s4，其中，s1=0.9，s2=s1-PL，s3=s2-PI2=PI3。

状态转移方程为

阶段指标函数为

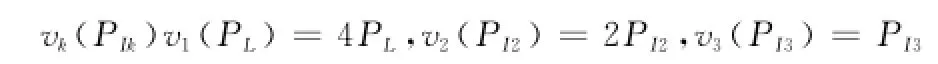
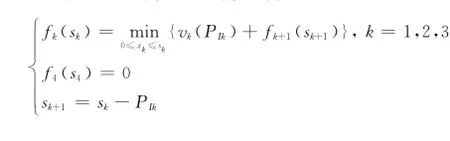
可得此问题的动态规划模型为也就是说，模型有无穷多最优解。只需要满足条件

因为在满足最小费用的前提下，平均隔离模糊度¯L越小越好，也就是说，在费用代价相同的情况下，故障隔离的越小越有利于进行后续的维修等工作。

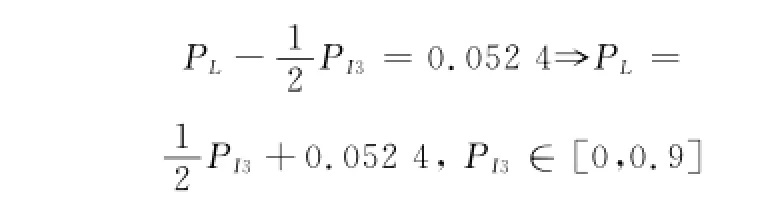
由最小费用模型的最优解可导出故PL的取值范围为［0.052 4，0.9］，则

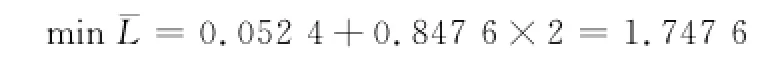
此时优化结果为（0.052 4，0.847 6，0），C=1.904 8。与逐步寻优算法是一致的。

7　分析结论汇总

根据以上分析、建模与优化计算，可以得出以下结论：

（1）装备的故障隔离模糊度或允许的L值，不能仅仅用单个数值来描述，而应当采用3个数值来描述：最大值Lmax、最小值Lmin和平均值¯L。如果给出单个数值表示，其实际含义应是平均值¯L。

（2）如果因为条件限制而只能进行定性分析的话，那么其取值规则一般应是Lmax=3，Lmin=1。至于其均值应取多少，则一般应通过类比分析得到，或根据估计而初步得到一个数值，例如¯L=1.50，并随着装备研制活动的开展而逐步使之精确化。

（3）在条件具备时，故障隔离模糊度应通过定量优化的方式确定。如已知装备的MTTR和其对应的结构组成分量tIN、tO，并通过FMECA分析等形式确定或估计得到其IFIG指标（αL、αI2、αI3），就可以进行优化计算，分别得到故障隔离百分比分配到各个隔离模糊度的数值，并计算出故障隔离模糊度的定量指标（均值）。

进一步的建模和分析表明（分析过程略），以上结论对于故障隔离模糊度有更多分量（包括PI4或更多）时仍然成立。

（4）本文的分析表明，要完整地确定装备的测试性指标，离不开装备的维修时间和维修时间结构分析。从这个意义上来讲，装备的测试性指标应当取自维修性定量分析，而测试性指标应是维修性指标的一种延伸和深化。

（5）在装备研制过程中，进行FMECA是一个很重要的过程，从其中得到的各类信息，可以用于确定测试性指标的定性分析时的粗略结论，也可以用于定量优化和计算。

8　结　论

完整的故障隔离率指标包括故障隔离百分比和隔离模糊度两个部分，本文结合当前的研究现状（对于前者的研究已经较为成熟），针对后者进行了初步的分析和优化研究。在装备研制的早期阶段，在确定故障隔离百分比要求的同时，合理地规定故障隔离模糊度，以便于作为装备研制后续阶段的测试性设计的依据和指导性要求，并以较为合理的设计措施和成本来实现和达到这一指标，是一个很有价值的问题。

本文从装备故障隔离指标的基本定义和初始分析出发，针对在装备研制早期，已经给定故障隔离百分比后，如何确定对应的故障隔离度问题，借助于装备测试性设计和分析中的MSFG及其示例计算结果，结合测试性设计中故障模糊度的不同分布，得到了装备故障隔离模糊度的完整的度量指标（包括最小值、最大值、均值），以及当前指标的物理意义（单个指标应理解为均值）。对于缺乏定量数据支撑从而只能进行定性分析的情况（例如TRL＜6时），本文通过对于典型案例的综合分析，给出了最小值、最大值和均值确定的方法和原则。在定量分析方面，通过装备维修和故障隔离过程分析，建立了故障隔离模糊度的通用优化模型，其指导思想是对于指定的故障隔离百分比和平均修复时间，使实现指定的故障隔离百分比的成本最低。在模型求解方面，首先对模型进行了工程应用简化，给出了模型优化解存在的前提条件，通过逻辑分析等手段，结合典型示例给出了优化模型求解的逐步寻优算法和动态规划算法，应用本文的模型和优化算法可以得到对于指定的故障隔离百分比，经过优化的故障隔离模糊度的最小值、最大值和均值的精确解。从而在工程应用的背景下，较为圆满地解决了这一问题。该方法结合与之配套的相关研究成果已用于海军某装备测试性指标论证和测试性设计工作中，取得了极其明显的效益。

［1］Izosimov V，Ingelsson U.Requirement decomposition and testability in development of safety-critical automotive components［J］.Lecture Notes in Computer Science，2012，76（1）：87-98.

［2］Sohn S D，Seong P H.Quantitative evaluation of safety critical software testability based on fault tree analysis and entropy［J］.Journal of Systems and Software，2004，73（2）：351-360.

［3］Shi J Y，Wang L，Li HW，et al.Quantitative analysis of system testability based on design characteristics［J］.Systems Engineering and Electronics，2012，34（2）：418-423.（石君友，王璐，李海伟，等.基于设计特性覆盖的测试性定量分析方法［J］.系统工程与电子技术，2012，34（2）：418-423.）

［4］Dendouga A，Hafiane M L，Bouguechal N，et al.Analog design-for-testability technique for first-order sigma delta ADC［J］. Measurement，2013，46（9）：3342-3346.

［5］Tan X D，Qiu J，Liu GJ，et al.A novel approach of testability modeling and analysis for PHM systems based on failure evolution mechanism［J］.Chinese Journal of Aeronautics，2013，26（3）：766-776.

［6］Vorobev G V，Pshenichnaya K S.Methodology of the system analysis of the influence of testability indicators on the usage efficiency of aircraft weapons systems［J］.Journal of Computer and Systems Sciences International，2012，51（5）：663-680.

［7］Nayak A，Samanta D.Synthesis of test scenarios using UML activity diagrams［J］.Software and Systems Modeling，2011，10（1）：63-89.

［8］Zhang Y S，Huang K L，Chen J H.Research on determining TFOMs of complex equipment［J］.Journal of Ordnance Engineering College，2010，22（6）：7-10.（张延生，黄考利，陈建辉.复杂装备测试性指标确定方法研究［J］.军械工程学院学报，2010，22（6）：7-10.）

［9］Baldini A，Prinetto P，Denaro G，et al.Design for testability for

highly reconfigurable component-based systems［J］.Electronic

Notes in Theoretical Computer Science，2003，82（6）：199-208.

［10］Cheng H，Mats N，Sirkka-Liisa J J.Evaluation of PCA methods with improved fault isolation capabilities on a paper machine simulator［J］.Chemometrics and Intelligent Laboratory Systems，2008，92（2）：186-199.

［11］Li Z Y，Huang K L，Lian G Y，et al.A method of extended testability modeling based on fault injection system［C］//Proc. of the 2nd International Conference on Electronic and Mechanical Engineering and Information Technology，2012：2151-2154.

［12］Van den Kerkhof P，Vanlaer J，Gins G，et al.Analysis of smearing-out in contribution plot based fault isolation for statistical process control［J］.Chemical Engineering Science，2013，104（50）：285-293.

［13］Tan H，Peng M F.Minimization of ambiguity in parametric fault

diagnosis of analog circuits：a complex network approach［J］.Ap

plied Mathematics and Computation，2012，219（1）：408-415.

［14］Lin Z W，He Z，Yang S Y.Multi-signal model based method for radar testability analysis［J］.Systems Engineering and E-lectronics，2009，31（11）：2781-2784.（林志文，贺喆，杨士元.基于多信号模型的雷达测试性设计分析［J］.系统工程与电子技术，2009，31（11）：2781-2784.）

［15］Tan Y H，He Y G，Sun Y C.Design of test stimuli and minimization of ambiguity in fault diagnosis of analogue circuits with tolerance［J］.International Journal of Electronics，2011，98（2）：173-183.

［16］Gonzalez S A，Rui A，Gross H G，et al.Prioritizing tests for fault localization through ambiguity group reduction［C］//Proc.of the 26th IEEE/ACM International Conference on Automated Software Engineering，2011：83-92.

［17］Lee E S，Heo M B.A fault tolerance method using the multiple hypotheses Wald sequential probability ratio test for integer ambiguity resolution［D］.Deajon：Korea Aerospace Research Institute，2009.

［18］Huang X，Lian G Y，Chang T Q，et al.Study on optimization method based on technology readiness assessment and binary particle swarm optimization for equipment test design［J］.Acta Armamentarii，2011，32（2）：1171-1176.（黄鑫，连光耀，常天庆，等.基于技术成熟度和二进制粒子群优化算法的装备测试设计优化方法研究［J］.兵工学报，2011，32（2）：1171-1176.）

［19］Liu G，Li F，Hu B.Test and modeling of vessel equipment based on relevant model［J］.Journal of Naυal Uniυersity of Engineering，2012，24（8）：46-51.（刘刚，黎放，胡斌.基于相关性模型的舰船装备测试性分析与建模［J］.海军工程大学学报，2012，24（8）：46-51.）

［20］Zhang Y，Ma Y H，Li G，et al.Research on testability in radar BIT based on multi-signal model［J］.Computing Technology and Automation，2012，31（1）：39-43.（张晔，马彦恒，李刚，等.基于多信号流模型的雷达BIT测试能力分析［J］.计算技术与自动化，2012，31（1）：39-43.）

［21］Tian F F，Gao Y J.Testability analysis and evaluation for photoelectric radar system based on multi-signal model［J］.Aυiation Maintenance&Engineering，2013，5：62-64.（田斐斐，高雅娟.基于多信号模型的光电雷达系统测试性设计分析与评价［J］.航空维修与工程，2013，5：62-64.）

［22］Zhou D X，Song MY，Zhan X L.Research of aircraft units testability based on improved extended dependency model［J］. Computer Measurement&Control，2012，20（12）：3176 3178.（周德新，宋明瑜，詹湘琳.基于改进扩展关联模型的飞机组件测试性研究［J］.计算机测量与控制，2012，20（12）：3176-3178.）

［23］Liu B H.Research on technology of hierarchical fault diagnosis on electronic equipment［J］.Computer Measurement&Control，2013，21（2）：297-311.（刘葆华.电子装备层次化故障诊断技术研究［J］.计算机测量与控制，2013，21（2）：297-311.）

［24］Chen X X，Qiu J，Liu G J.Research on technologies of optimal testability concept for materiel systems［J］.China Mechanical Engineering，2010，21（2）：141-145.（陈希祥，邱静，刘冠军.装备系统测试性方案优化设计技术研究［J］.中国机械工程，2010，21（2）：141-145.）

［25］Lv J W，Liu Z H，Yang JJ，et al.A structural approach to assessment of technical risk in major navy vessel's development［J］.Systems Engineering-Theory&Practice，2012，32（10）：2339 2344.（吕建伟，刘中华，杨建军，等.大型海军舰船研制技术风险综合评估的一种结构化方法［J］.系统工程理论与实践，2012，32（10）：2339-2344.）

谢宗仁（1990-），通讯作者，男，博士研究生，主要研究方向为复杂系统建模与仿真。

E-mail：wx18392015@163.com

徐一帆（1981-），男，讲师，博士，主要研究方向为系统优化与综合集成、风险管理。

E-mail：boat_xu@nudt.edu.cn

Requirement's determining and optimization on fault isolation's ambiguity group size of weapon system

LÜJian-wei，XIE Zong-ren，XU Yi-fan
（Department of Management Science，Naυal Uniυersity of Engineering，Wuhan 430033，China）

From the basic definition and analysis of fault isolation rate as a beginning，aiming at the early stage of weapon system development，after giving the percent of fault isolation，how to determine and optimize the corresponding fault isolation ambiguity group size is explored.Firstly，with the help of the multi-signal flow graph（MSFG）in the testability analysis and a typical example，and with different distribution of the fault isolation's ambiguity group in the testability design，the full measurement of the fault isolation ambiguity group size is found out，that it should be a group of sizes included maximum，minimum and average size.And a single size，currently being used by people，should be considered as an average value.To qualitative analyze when lacking information，with a typical example，the method and principle to determine we presented maximum，minimum and average size of the fault isolation ambiguity group size，on the condition of giving the fault isolation percent.To quantitative analyze，through analyzing the process of equipment repairing and fault isolation，a general optimization model about the fault isolation ambiguity group size is established.As how to get the optimization solution，firstly the general model by the background of engineering practice is simplified，and the condition that the optimization solution exist is presented.Then through the logical and mathematics analysis，taking typical equipment's repairing as an example，a method of step-by-step seeking for the optimization solution and an algorithm based on dynamic programming are completed.Using the models and methods，one can obtain the optimized accurate value of maximum，minimum and average size of the fault isolation ambiguity group size，on the condition of giving the fault isolation percent.So the problem about the fault isolation's ambiguity group size can be solved entirely on the engineering background.

early stage of development；testability analysis；fault isolation；ambiguity group size；optimization model

TJ 02；E 920

A

10.3969/j.issn.1001-506X.2016.05.36

1001-506X（2016）05-1208-07

2015-07-30；

2015-11-16；网络优先出版日期：2016-02-17。

网络优先出版地址：http：//www.cnki.net/kcms/detail/11.2422.TN.20160217.1409.006.html

国家自然科学基金（71401171）；总装预研基金（9140A19030214JB11273）；军队院校2110工程III期建设基金（4142D4A3）资助课题

吕建伟（1962-），男，教授，博士，主要研究方向为装备系统分析、风险分析与控制。

E-mail：l2015wh@163.com