模型诊断用于近红外光谱建模校正集中奇异样本的识别

李正风徐广晋王家俊杜国荣蔡文生邵学广*，（云南中烟工业有限责任公司技术中心，昆明 650）（南开大学化学学院，分析科学研究中心，天津 0007）（喀什大学化学与环境科学学院，喀什 844000）

研究简报

模型诊断用于近红外光谱建模校正集中奇异样本的识别

李正风1徐广晋1王家俊1杜国荣2蔡文生2邵学广*2，31
（云南中烟工业有限责任公司技术中心，昆明 650231）2（南开大学化学学院，分析科学研究中心，天津 300071）3（喀什大学化学与环境科学学院，喀什 844000）

由于校正集样本的质量决定校正模型的质量，校正集中奇异样本的检测在多元校正建模中具有非常重要的意义。本研究建立了一种用于近红外光谱多元校正建模时校正集中奇异样本的检测方法。本方法基于奇异样本的定义和偏最小二乘方法的原理，通过考察每个校正集样本在模型的每个因子（或主成分）中对模型的贡献，将与多数样本表现不同的样本识别为奇异样本。采用218个橘汁样本构成的近红外光谱数据进行了分析，结果表明，校正集中存在6个奇异样本，扣除奇异样本后，校正集的交叉验证均方根误差由16.870减小为4.809，预测集的均方根误差从3.688减小为3.332。

多元校正；奇异样本检测；偏最小二乘；近红外光谱；定量分析

1 引言

近红外光谱已在许多科研领域和行业得到广泛应用，多元校正是近红外光谱分析的的关键技术。已报道的多元校正方法有多元线性回归（MLR）、主成分回归（PCR）、偏最小二乘回归（PLSR）［1，2］、支持向量机（SVM）［3～5］等。为了提高建模方法的适用性，非线性建模、局部回归、多模型共识建模等方法与技术得到了发展与应用［6］。同时，为了提高模型的质量，改善模型的预测能力，建立精简模型，发展了一系列光谱预处理及变量选择技术，如多元散射校正（MSC）、正交信号校正（OSC）［7］、小波变换（WT）［8］、区间偏最小二乘回归（iPLSr）［9］、无信息变量消除（UVE）［10，11］、竞争性自适应权重取样（CARS）［12］、连续投影算法（SPA）［13］、随机检验（RT）［14］等。

校正集同样是决定模型质量的重要因素。多元校正的校正集一般由大量的样本构成，奇异样本的识别是多元校正分析中的难点问题之一［15］，因此，已建立了一系列方法，并在近红外光谱分析中得到应用［16～19］。当奇异样本之间无相互影响时，这些方法可以有效识别奇异样本。但是当奇异样本之间相互影响，如存在掩蔽（Masking）和淹没（Swamping）现象时，这些方法的识别能力受到限制［18，19］。稳健建模是一种可以自动识别奇异样本的方法，也可以用于处理奇异样本之间有相互作用的数据，例如稳健偏最小二乘回归（Robust simple partial least squares，RSIMPLS）［20］是一种简便、快速的常用方法。该方法通过诊断图识别建模样品中的好的杠杆点（Good leverage）、坏的杠杆点（Bad leverage）及残差方向放入奇异样本（Vertical outlier）。杠杆点是与大多数样本不一样的样本，好的杠杆点对校正模型起积极作用，坏的杠杆点降低校正模型的预测精度。残差方向的奇异样本是有较大浓度预测残差的样本。

本研究建立了一种新的奇异样本识别方法。基于奇异样本与其它样本在偏最小二乘回归模型中的作用不同，通过考察每个校正集样本在模型的每个因子（或主成分）中对模型的贡献，将与其它（多数）样本表现不同的样本识别为奇异样本。由于样本对偏最小二乘回归模型的贡献可以用其权重进行衡量，通过考察样本在每个因子中的权重分布即可实现奇异样本的识别。本方法的实质是对模型的每个因子进行分析，因此被称为“模型诊断”方法。

2 原理

奇异样本是指数据集中与其它（大量）样本不同的样本。在多元校正分析中，奇异样本是指在模型中与其它（大量）样本规律不同的样本，通常被认为是对模型具有破坏作用的样品。奇异样本分为“好的”和“坏的”奇异样本，前者对模型有好的影响，而后者对模型具有破坏作用，所以也称为强影响点［17，21］。本研究中，奇异样本是指在数据集中与其它（大量）样本在模型中的表现不同的样本。

偏最小二乘模型由多个因子（或主成分，又称为潜变量）构成，样本对模型的贡献取决于样本在每个因子中的权重。对于大部分（正常）样本，权重值在每个因子的分布在一个正常的区间里，而对于奇异样本，在某些因子中的权重将与其它（正常）样本不同。因此，通过对每个因子的权重分布考察就可以找到与其它（大量）样本有较大差异的样本，即奇异样本。

为了详细描述本方法的原理，用高斯函数模拟了6种物质的光谱图，并添加了1.0%的随机噪声。用第4个组分建立偏最小二乘回归模型，得到的每个样本在每个因子中的权重如图1a所示。所谓权重是指偏最小二乘在预测时对预测结果的贡献。由于建模时光谱和浓度进行了中心化，这些权重值在0上下分布。从图1a可见，前6个因子对预测结果有显著的贡献，通过分析对模型有显著贡献的因子可以用于因子数的判定［22］。由于没有奇异样本，图1a所有样本权重的分布比较均匀，说明正常样品在每个因子下的权重分布具有较高的相似性。

为了考察奇异样本对模型的影响，在10，20和30号样品的浓度值中添加了3倍标准偏差的变动，在40和50号样品的光谱中添加了与浓度无关的光谱信息。图1b为添加奇异样本后每个样本在不同因子中的权重分布。与图1a相比，添加奇异样本后因子数增加，需要更多的因子对模型进行描述。同时，奇异样本（图中标示的10，20，30，40和50）的权重在第6和7个因子中与其它样本具有明显差异。

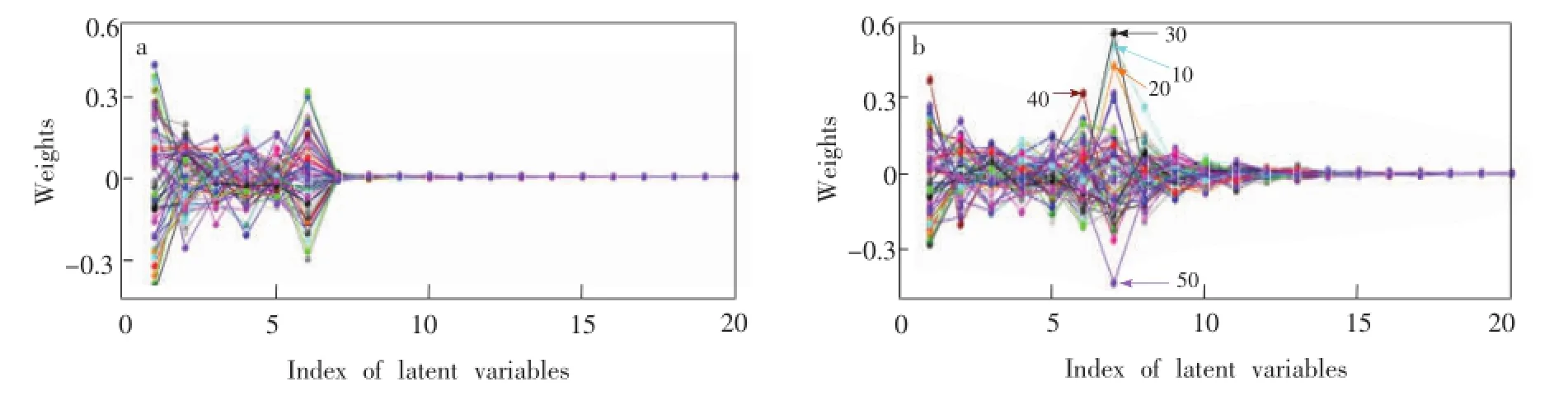
图1 模拟光谱数据偏最小二乘模型的权重分布Fig.1 Weights of each sample in each factor in PLS model of simulated spectra

为了对奇异样本进行识别，本研究引入LOF （Local outlier factor）［23］方法。LOF方法通过每个数据点附近的数据点数（密度）判断此数据点是否与其它数据点一致。图2是图1b中各样本的LOF值，5个奇异样本都可以很明显的识别出来。图 2的虚线为阈值，用正常样本LOF值平均值加3倍标准偏差计算得到。

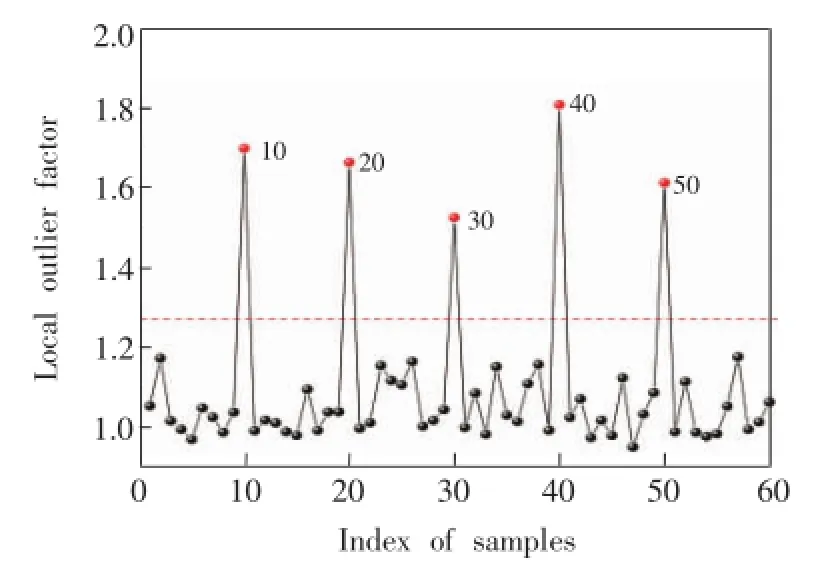
图2 具有奇异样本的模拟光谱数据中每个样本的LOF值Fig.2 Local outlier factor（LOF）values for samples in simulated spectra with artificial outliers

3 结果与讨论

3.1 数据来源与处理

本研究使用了一组包括218个橘汁样品的近红外光谱数据，建模的目标值为蔗糖含量［24］。数据可从http：//www.ucl.ac.be/mlg下载。光谱采用透射模式，波长范围为1100～2500 nm，间隔为2 nm。为了便于比较，校正集和预测集采用了数据提供者对光谱数据进行的分组，即校正集包括150个样品，预测集包括68个样品。为了消除噪声、背景对结果的影响，在计算前采用了Haar连续小波变换方法进行了预处理［8，17，21，22］，尺度参数为20。

3.2 奇异样本的识别

图3是利用校正集的数据建立的偏最小二乘模型中每个样本在每个因子中的权重分布。首先，此图显示对模型贡献较大的因子是第1，3，4，5，6和7，说明此模型的最佳因子数为8或9。第二个因子对模型的贡献很小，可能是由于该主成分与蔗糖的含量关系不大。比较每个样本在不同因子时的权重可知，第133和150个样本在第1主成分时、第130个样本在第2和3主成分时、第78个样本在9主成分时分别与其它样本有很大差异。因此，这些样本可能是校正集中的奇异样本。

为了更加明确地确定奇异样本，根据图3的数据可以计算每个样本的LOF值，如图4。图4中的红色虚线为阈值，由LOF值的平均值和标准偏差确定。从图4中可清楚地看出，共有6个奇异样本，分别是第36，78，130，133，140及150个校正集样本。

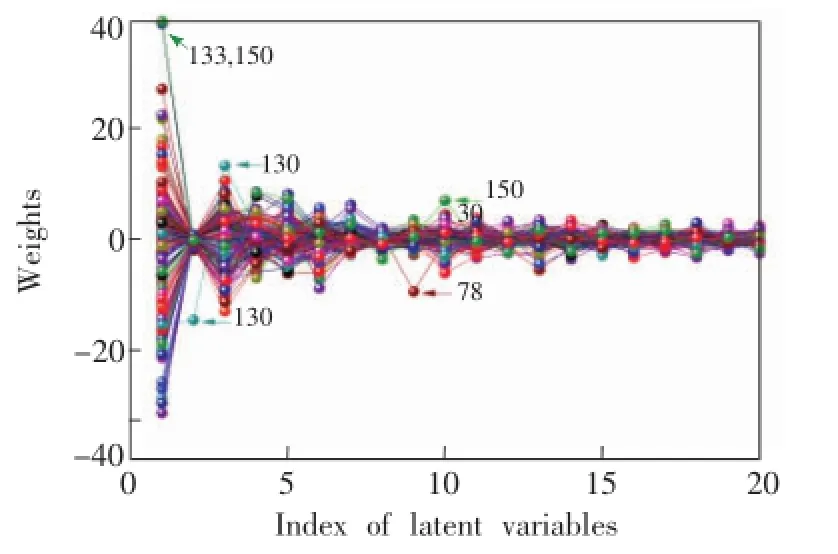
图3 校正集样本偏最小二乘模型的权重分布Fig.3 Weights of calibration samples in each factor of PLS model

图4 校正集中每个样本的LOF值Fig.4 LOF values for samples in calibration set

3.3 模型诊断方法的性能比较

为了考察模型诊断方法奇异样本识别结果的正确性，分别与常用的留一交叉验证-3倍标准偏差法和稳健回归诊断（RSIMPLS）方法进行了比较。留一交叉验证方法只识别出一个（第130个）奇异样本，即只有一个样本在交叉验证中预测误差超出了其它样本预测误差的3倍。采用RSIMPLS方法的回归诊断图（Regression diagnostic plot）［20］找到了23个奇异样本，其中第130个样本与其它样本有显著的差异。

比较模型诊断、留一交叉验证和稳健回归诊断3种方法可知，留一交叉验证方法过于“宽松”，原因可能是奇异样本较多时留一交叉验证预测误差的标准偏差较大。稳健回归诊断方法过于“严格”，原因可能是阈值过小，Χ2分布在样本量较大时相关参数需要调整。相比之下，模型诊断方法得到结果相对较为合理。值得注意的是模型诊断方法识别的6个奇异样本中有5个被该方法识别，只有第36个样本未被识别，而留一交叉验证方法所识别的第130个样本同时被3种方法识别。此结果说明不同识别方法均具有一定的科学性，只是在识别“灵敏度”上具有差异。

3.4 奇异样本对模型的影响

为了进一步考察奇异样本识别结果的正确性，分别考察了所识别的奇异样本对模型及预测结果的影响。表1列出了移除一个或几个奇异样本后交叉验证均方根误差（RMSECV）和样本预测误差的均方根误差（RMSEP）的变化情况，其中RMSEP1为全体预测集样本的预测结果，RMSEP2为扣除4个预测误差较大的样本（疑为预测集中的奇异样本）后的预测结果。第一行为参考值，未扣除奇异样本；第二行中第130个样本对RMSECV的影响很大，扣除该样本后RMSECV的数值有大幅度的降低，但是对预测集的预测结果并没有产生大的影响。这种现象可以通过PLS的原理进行解释。从图3可见，第130个样本对模型的影响主要体现在第二个因子，比其它样本偏低，在第3个因子中则有些偏高，第4个因子以后不再偏离。PLS的预测结果是多个因子预测结果的加和，当采用较大的因子数时，第130个样本对模型的整体影响被抵消。为了验证这一推测，比较了扣除第130个样本前后因子数为2和7时的模型系数，结果表明，因子数为2时，有明显差异而因子数为7时差异并不大。因此，第130个样本对于因子数较大的模型并没有产生较大影响。

从表1第3行的结果可知，第78个样本对RMSECV的也有一定程度的影响，RMSEP1的数值有所上升，但RMSEP2的结果有较大幅度下降。前者说明预测集中具有奇异样本，后者说明第78个样本确实对模型具有一定影响。通过表1中第4～7行的结果可知，第133和150个样本使RMSECV降低，第36和140个样本使RMSECV升高，但RMSEP2的结果均没有下降。为了考察奇异样本之间的“掩蔽”或“淹没”效应，表1中第8～12行分别列出了多个奇异样本同时扣除时多模型的影响。从RMSECV的结果可知，奇异样本之间的协同作用，但从RMSEP2的结果第78个样本具有较大的影响。因此，本组数据中对模型影响最大的奇异样本应该只有第78个样本。从奇异样本对模型及预测能力的影响可以看出，奇异样本的检测是一项非常困难的任务，仅从模型自身的评价（RMSECV）难以对模型的预测能力进行估计。当预测集（检验集）中存在奇异样本时，也难以得到正确的评价。

表1 奇异样本对模型及预测结果的影响Table 1 Effect of detected outliers on model and prediction result

4 结论

建立了一种基于模型诊断的奇异样本识别方法，通过建模样本在每个因子中对模型的贡献，将模型中权重分布不同的样本识别为奇异样本。与常用的留一交叉验证和稳健回归诊断方法进行比较，表明本方法具有一定的合理性和实用性。但是，奇异样本对模型及预测能力的影响具有较高的复杂性，单独使用模型的检验无法表明模型预测能力，采用验证集进行评价时必须保证验证集的质量。因此，奇异样本的检测与识别仍然是一项非常艰巨的任务，有待进一步的深入研究，提出更加科学、可靠的更多方法。

1 Wold S，Ruhe A，Wold H，Dunn W J.SIAM J.Sci.Stat.Comput.，1984，5（3）：735-743

2 LIANG Miao，CAI Jia-Yue，YANG Kai，SHU Ru-Xin，ZHAO Long-Lian，ZHANG Lu-Da，LI Jun-Hui.Chinese J.Anal. Chem.，2014，42（11）：1687-1691

梁淼，蔡嘉月，杨凯，束茹欣，赵龙莲，张录达，李军会.分析化学，2014，42（11）：1687-1691

3 ZHANG Lu-Da，SU Shi-Guang，WANG Lai-Sheng，LI Jun-Hui，YANG Li-Ming.Spectroscopy and Spectral Analysis，2005，25（1）：33-35

张录达，苏时光，王来生，李军会，杨丽明.光谱学与光谱分析，2005，25（1）：33-35

4 Li Y K，Shao X G，Cai W S.Talanta，2007，72（1）：217-222

5 LIN Hao，ZHAO Jie-Wen，CHEN Quan-Sheng，CAI Jian-Rong，ZHOU Ping.Spectroscopy and Spectral Analysis，2010，30（4）：929-932

林颢，赵杰文，陈全胜，蔡健荣，周平.光谱学与光谱分析，2010，30（4）：929-932

6 Shao X G，Bian X H，Liu J J，Zhang M，Cai W S.Anal.Methods，2010，2（11）：1662-1666

7 Wold S，Antti H，Lindgren F，Ohman J.Chemom.Intell.Lab.Syst.，1998，44（1-2）：175-185

8 Shao X G，Leung A K M，Chau F T.Acc.Chem.Res.，2003，36（4）：276-283

9 Norgaard L，Saudland A，Wagner J，Wagner J，Nielsen J P，Munk L，Engelsen S B.Appl.Spectrosc.，2000，54（3）：413-419

10 CentnerV，Massart D L，de Noord O E，de Jong S，Vandeginste M B，Sterna C.Anal.Chem.，1996，68（21）：3851-3858

11 Cai W S，Li Y K，Shao X G.Chemom.Intell.Lab.Syst.，2008，90（2）：188-194

12 Li H D，Liang Y Z，Xu Q S，Cao D S.Anal.Chim.Acta，2009，648（1）：77-84

13 Araujo M C U，Saldanha T C B，Galvao R K H，Yoneyama T，Chame H C，VisaniV.Chemom.Intell.Lab.Syst.，2001，57（2）：65-73

14 Xu H，Liu Z C，Cai W S，Shao X G.Chemom.Intell.Lab.Syst.，2009，97（1）：189-193

15 Liang Y Z，Kvalheim O M.Chemom.Intell.Lab.Syst.，1996，32（1）：1-10

16 Pierna J A F，Jin L，Daszykowski M，Wahl F，Massart D L.Chemom.Intell.Lab.Syst.，2003，68（1-2）：17-28

17 Bian X H，Cai W S，Shao X G，Chen D，Grant E R.Analyst，2010，135（11）：2841-2847

18 Pierna J A F，Wahl F，de Noord O E，Massart D L.Chemom.Intell.Lab.Syst.，2002，63（1）：27-39

19 Walczak B，Massart D L.Chemom.Intell.Lab.Syst.，1998，41（1）：1-15

20 Hubert M，Vanden Branden K.J.Chemom.，2003，17（10）：537-549

21 Liu Z C，Cai W S，Shao X G.Sci.China Ser B-Chem.，2008，51（8）：751-759

22 Liu Z C，Ma X，Wen Y D，Wang Y，Cai W S，Shao X G.Sci.China Ser B-Chem.，2009，52（7）：1021-1027

23 Breunig M M，Kriegel H P，Ng R T，Sander J.Sigmod.Rec.，2000，29（2）：93-104

24 Li W，Goovaerts P，Meurens M.J.Arg.Food Chem.，1996，44（8）：2252-2259

This work was supported by the National Natural Science Foundation of China（No.21475068）and the Major Project of China National Tobacco Corporation（No.Ts-03-20110020）.

Outlier Detection for Multivariate Calibration in Near Infrared Spectroscopic Analysis by Model Diagnostics

LI Zheng-Feng1，XU Guang-Jin1，WANG Jia-Jun1，DU Guo-Rong2，CAI Wen-Sheng2，SHAO Xue-Guang*2，31（R&D Center，China Tobacco Yunnan Industrial Co.Ltd.，Kunming 650231，China）
2（Research Center for Analytical Sciences，College of Chemistry，Nankai University，Tianjin 300071，China）
3（College of Chemistry and Environmental Science，Kashgar University，Kashgar 844000，China）

Outlier detection is an important task in multivariate calibration because the quality of a calibration model is determined by that of the calibration data.An outlier detection method is proposed for near infrared （NIR）spectral analysis.The method is based on the definition of outlier and the principle of partial least squares（PLS）regression，i.e.，an outlier in a dataset behaves differently from the rest，and the prediction result of a PLS model is an accumulation of several independent latent variables.Therefore，the proposed method builds a PLS model with a calibration dataset，and then the contribution of each latent variable is investigated.Outliers can be detected by comparing these contributions.An NIR spectral dataset of orange juice samples is adopted for testing the method.Six outliers are detected in the calibration set.The root mean squared error of cross validation（RMSECV）becomes to 4.809 from 16.870 and the root mean squared error of prediction（RMSEP）becomes to 3.332 from 3.688 after the removal of the outliers.Compared with a robust regression method，the result of the proposed method seems more reasonable.

Multivariate calibration；Outlier detection；Partial least squares；Near infrared spectroscopy；Quantitative analysis

11 October 2015；accepted 28 October 2015）

10.11895/j.issn.0253-3820.150793

2015-10-11收稿；2015-10-28接受

本文系国家自然科学基金项目（No.21475068）和中国烟草总公司重大专项课题（No.Ts-03-20110020）资助

*E-mail：xshao@nankai.edu.cn.