基于DEA模型和SFA模型的高职院校效率评价研究

相旭东，李泽圣，胡学平

(安庆师范大学 数学与计算科学学院，安徽 安庆246133)



基于DEA模型和SFA模型的高职院校效率评价研究

相旭东，李泽圣，胡学平*

(安庆师范大学 数学与计算科学学院，安徽 安庆246133)

数据包络分析(DEA)和随机前沿分析(SFA)各有优缺点，本文将DEA模型与SFA模型分别与因子分析相结合，以福建省15个高职院校为例，对高职院校效率评估进行实证分析，根据分析结果对有关院校的情况提出了整改对策。

因子分析；随机前沿分析；数据包络分析；效率评价

近几年来，我国高职教育受到广泛关注。直到2012年秋季，高职高专层次招生数在高校招生中占据了一半以上，在国家政策的大力扶持下，高职教育对人才的培养能力得到极大提升。然而，部分学校在许多方面仍然存在不足，“双师型”专业教师数量过少，办学机制改革方面也有待加强。因此，为了迎合社会的需求，应该以基础能力建设为起点，深化内涵建设，提升教学质量，实现改革发展，加强训练高素质人才，使其能更好地在先进制造业、现代农业和服务业方面发挥作用。所以，为了使高等职业教育快速蓬勃发展，急需一套科学可行的评价体系，用以对高等职业教育进行效率评估，并提供指导。

1　因子分析、DEA模型和SFA模型的基本思想

因子分析法[1]是一种降维的常用手段，利用原始指标间的相关性，了解其基本结构，然后用少数公因子的线性组合来表示，其主要优点在于公因子的数目比原始指标少得多，把繁琐的处理过程变得相对简单。

数据包络分析[2](Data Envelopment Analysis，DEA)，是一种非参数的效率评估方法，其思想在于保持决策单元(DMU)的输入或输出不变的条件下，将其投影到相对有效的生产前沿面上，判断其偏离程度，即DEA是否有效，能够避免主观因素的影响，简化计算过程，减少可能存在的误差。本文所选用的模型为

(1)

其中θ为第i个DMU的技术效率值，满足0≤θ≤1；s为松弛变量；λj是一个N×1常数向量，Tj,Cj分别为投入产出。

随机前沿分析[3](Stochastic Frontier Analysis，SFA)，是一种参数方法，是前沿效率的评价方法之一。首先建立生产函数，以此为基础形成生产前沿面，求出技术无效率项的条件期望，用以作为技术效率，这种方法计算得到的结果受特殊点影响小，同时计算得到效率值不会相同并且不为1，相对DEA来说更为可靠，有可比性，然而，SFA不适合多产出的情况，对待多产出的问题需要将多产出合并，生成一个综合产出。

2　因子分析分别和DEA模型、SFA模型组合的效率评估

因子分析与DEA模型组合的效率评价方法步骤如下：

步骤1：使用因子分析对原始指标进行降维处理，转化为少数的具有明确经济意义的公共因子，根据每个决策单元的因子得分对原始指标进行初步判断，以反映原始变量的实际水平。

步骤2：由于DEA模型在计算过程中要求数据必须为正，因此，为了满足DEA模型的需求，使用极差变化法进行变量的正向化处理。

步骤3：分别使用D(C2R)输入模型和BCC输出模型[3]对各个决策单元进行计算处理，得出每个决策单元的技术效率值，同时由模型计算所得的结果对规模收益情况进行分析。

步骤4：分析研究非DEA有效的决策单元，利用投影定理提出改进建议，找出决策单元非DEA有效的原因和改进的方向。

因子分析与SFA模型组合的效率评价方法步骤如下：

步骤1：使用因子分析对原始指标进行降维处理，转化为少数的具有明确经济意义的公共因子，根据每个决策单元的因子得分对原始指标进行初步判断，以反映原始变量的实际水平。

步骤2：使用SFA模型对各个决策单元进行计算处理，得到各个决策单元的技术效率值以及各待估参数。

步骤3：通过计算结果分析各个决策单元的技术效率水平及其描述性统计结果。

3　实例分析

本文以福建省2013年度15所示范性高职院校内涵建设指标数据[4]为基础，根据因子分析法分别和DEA模型以及SFA模型相结合进行实例分析。

依据高等院校效率评价体系的构建原则，所确定的效率评价体系指标应当包含教学水平、科学研究、财务收支、社会成果等多方面，各指标之间一方面彼此联系，另一方面又相互制约，各种因素在一起形成一个统一的综合系统。该综合系统从全方位多角度对效率进行评估分析，将单一因素紧密联系在一个彼此制约的系统中[5]。

3.1 因子分析和DEA模型组合实例分析

3.1.1 投入产出指标的选取

在对高职院校的投入指标分类中，可以从不同方面进行分类研究。从本质分类，包括人力投入和物质投入；从可视角度分类分为无形投入与有形投入[6]。本文以在校师生数、招生专业、大中型企业合作数、省级应用科技中心数、升级科研创新平台等作为投入指标进行分析计算。当今社会，我国高等院校大多以“产、学、研”作为发展道路，因此，产出指标主要反映教学水平、科学研究、毕业生对社会的贡献等多层次绩效，故选取毕业生双证书获取率、年度社会培训量、年度国家级大学生职业技能竞赛获奖、年度省级以上科研项目立项、招生计划实际完成率等作为产出指标。

3.1.2 评价过程

为了构造15个高职院校投入产出的因子变量，本文使用主成分分析法选取特征值大于1的6个变量作为新的因子变量，这6个因子的累计贡献率达到88.11%，包含了初始变量大部分信息。利用SPSS软件进行分析可得这6个因子变量的因子得分。由于DEA要求所有数据都必须为正数，故对每个DMU的因子得分做正向化处理。

代入模型(1)计算，结果见表1。表1第2列为C2R的计算值；第3列为C2R和BCC输出倾向模型计算所得的规模收益情况；第4-9列表示C2R模型计算的松弛变量值。

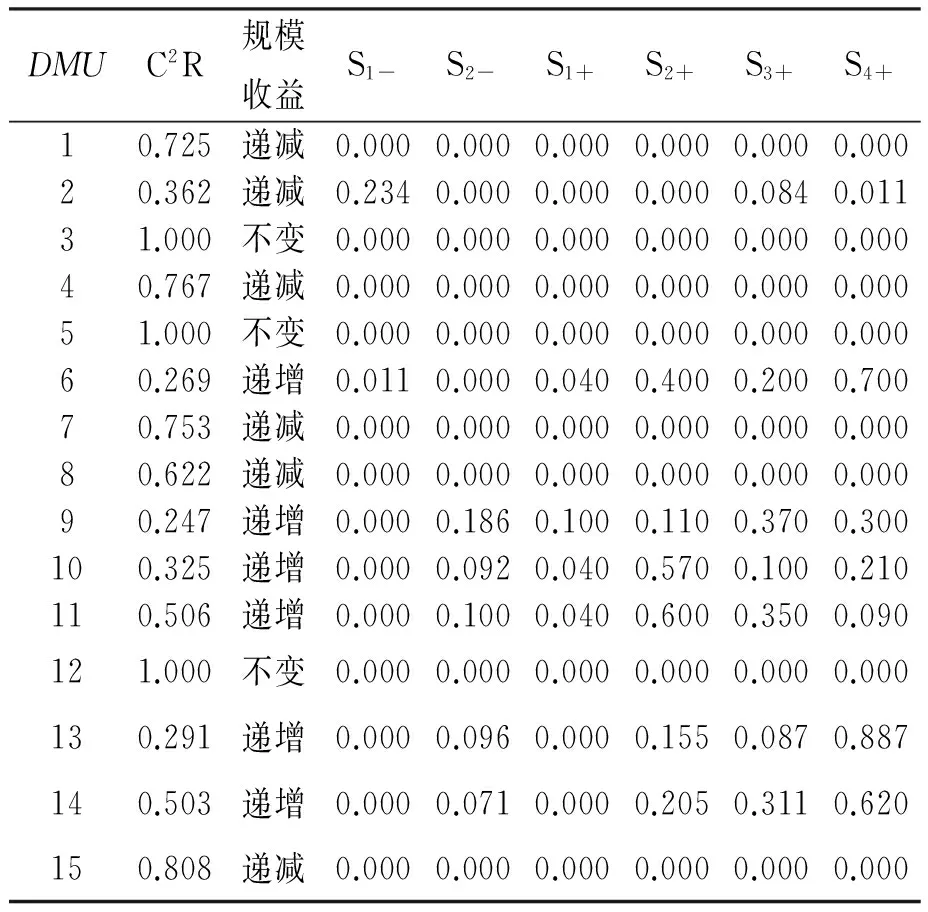
表1　DEA计算结果表

3.1.3 结果分析

(1)由表1得，15个高职院校中3个院校的效率值为1，松弛变量均为0并且规模收益不变，即这3个院校都是DEA有效的，此时这3个院校在学校建设和学校的规模收益上都处于最优状态。

(2)由表1得，效率值小于1的12个院校中，有6个院校的规模收益递减，而其他6个院校的规模收益递增，说明这15个院校中有6所非DEA有效的院校在学校建设和学校配置方面存在一定的问题。

(3)通过分析可得各非DEA有效DMU的改进值如表2。

表2　DEA改进值表

3.2因子分析和SFA模型组合实例分析

本文选取全日制在校生数、专任教师数、大中型企业合作数等指标作为投入指标，并进行因子分析得到因子得分。产出指标选取年度技术服务收入，得到投入产出。

文中使用Frontier(Version4.1)程序构建SFA模型，采用对数型Cobb-Douglas生产函数如下：

lnYi=b0+ajbjlnxij+vi+ui,i=1,…,N

使用Frontier(Version4.1)处理投入产出指标，得到表3和表4。

表3　对15个高职院校生产函数的估计

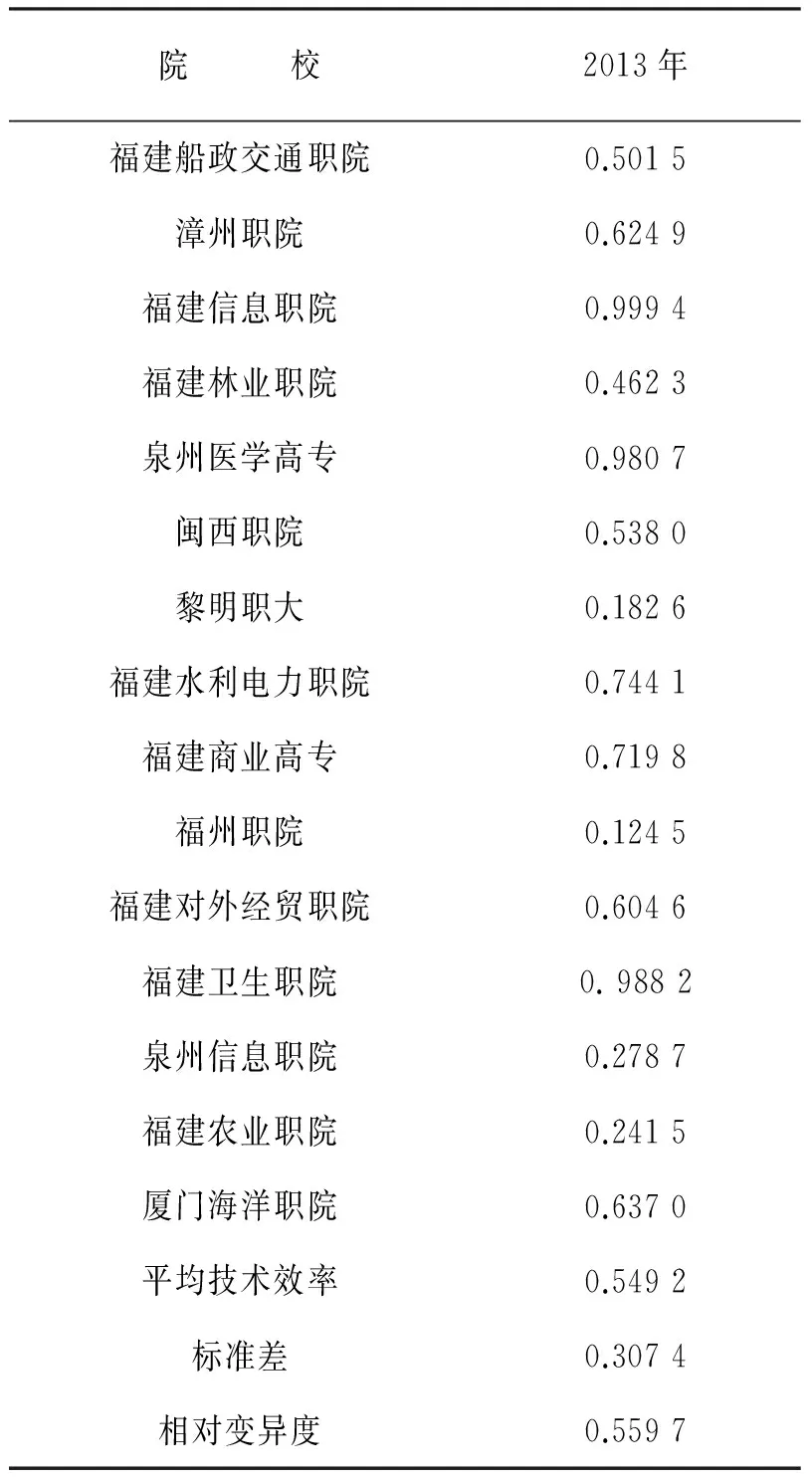
表4　15个高职院校技术效率水平及其描述性统计

注：平均技术效率为15个高职院校的算术平均值；标准差为15个高职院校的标准差；相对变异度=标准差/平均技术效率。

通过表3和表4可得：

(1)g=0.999 9，在1%的水平下LR统计检验是显著的，这说明模型中的误差项复合结构十分明显，所以，有必要对这些高职院校使用SFA技术。

(2)从师资、科研和教学三大要素的产出弹性来看，b1=120.654 7，b2=153.829 6，b3=48.212 7，即师资力量提升1%，则收入增长约120.654 7个百分点；科研提升增加1%，可促进服务收入增长153.829 6个百分点；教学水平提升1%，可促进服务收入增长48.212 7个百分点。

4　评价与比较

本文对福建省15个示范性高职院校进行效率评估，通过对因子分析分别与DEA模型、SFA模型相结合的方法分析研究可以发现，两种方法得出的效率值虽有差异，但反映的结果大致相同，各有优劣。由此可以得出DEA模型与SFA模型的不同点如下：

(1)两者对模型进行基本假设以及扩展过程的复杂程度存在较大差异。SFA模型比较复杂，误差项的合成密度函数形式较为复杂，对应的似然函数则更为复杂，故想要深入研究比较麻烦。而DEA模型的好处就在于不用去考虑生产函数，只要对投入产出指标进行处理，其模型扩展也很容易。

(2)SFA和DEA在处理解释实际产出时所用的方法不同。SFA运用极大似然估计求解，以技术无效率项的条件期望作为技术效率值，所以效率值一般情况下不会为1。DEA运用线性规划求解，所得结果至少有一个DMU的效率值为1。

(3)两种模型构建生产前沿的方法不同。DEA模型仅选用一个或几个DMU构建生产前沿，SFA模型使用生产函数结合随机扰动项，从而构造具有随机性的生产前沿。当样本容量较大时，大量的样本数据未必能满足DEA线性规划所做的基本假设，其计算结果会因此而失败，在这种情况下，SFA模型则能比较好的应对。

本文的研究为运用不同方法对高职院校效率评价研究提供了一种新的思路，并为高职院校科研管理与资金运营等各方面提供了有效的建议与指导，在实际生活应用中，可以针对不同的情况采用不同的方法进行有效分析，不能单方面认为哪种方法更好，而要针对问题的特点进行分析判断，通过实际计算和相关检验来决定到底使用哪种方法更合理有效。

[1] 上官飞, 舒长江. 基于因子分析的中国商业银行绩效评价[J]. 经济问题，2011(1): 109-111.

[2] 许楠. 基于SFA与DEA模型的创新型城市科技创新效率实证研究[J]. 数学的实践与认识，2011，41(18): 113-117.

[3] 何枫,陈荣,何炼成.SFA模型及其在我国技术效率测算中的应用[J].系统工程理论与实践，2004，24(5): 47-50.

[4]neuwhy22. 2013年度福建省普通高等学校内涵建设指标数据汇总(高职)[EB/OL]. (2014-07-01)[2016-4-7].http://wenku.baidu.com/link?url=ZDTpTUgtMxO5Bt1DJj

30XK2v8mHPdb92zaI9M9VfwFTupg0QFKwBwyH1jghmoeCgjQ_3-V7eU7Kj-uJ6XNPAHo7OBvJwzu8-yAXIMBGou5y.

[5]BelloneC.Publicentrepreneurship:newroleexpectationsforlocalgovernment[J].UrbanAnalysis, 1988, 9(1):271-277.

[6]CothranD.Entrepreneurialbudgeting:anmergingreform[J].PublicAdministrationReview,1993, 53(6): 445-454.

Efficiency Evaluation of Universities Based on DEA and SFA Model

XIANG Xu-dong, LI Ze-sheng, HU Xue-ping

(College of Mathematics and Computing Science, Anqing Normal University, Anqing, Anhui 246133, China)

The DEA(Data Envelopment Analysis) model and SFA(Stochastic Frontier Analysis) model have advantages and disadvantages respectively. The paper presents a method to evaluate the efficiency of Higher Vocational Colleges by combining factor analysis with DEA model and SFA model. The factor analysis is combined with DEA model and SFA model respectively. The paper analyzes the technical efficiency of the higher vocational colleges in Fujian province. According to the analysis results, some countermeasures are put forward.

factor analysis; Stochastic Frontier Analysis (SFA); Data Envelopment Analysis (DEA); efficiency evaluation

2016-04-09

安徽省精品资源共享课程项目(2015gxk045)和安庆师范大学创新创业项目(CXZ15017)。

相旭东，男，安徽亳州人，安庆师范大学数学与计算科学学院硕士研究生。E-mail: 929825036@qq.com

胡学平，男，安徽安庆人，博士，安庆师范大学数学与计算科学学院教授，研究方向为概率论与应用统计。E-mail: hxprob@163.com

时间：2016-8-17 11:31

http://www.cnki.net/kcms/detail/34.1150.N.20160817.1131.013.html

O212.1

A

1007-4260(2016)03-0043-04

10.13757/j.cnki.cn34-1150/n.2016.03.013