线性齐次型上的周期作用

孙 广 人

(安庆师范大学 数学与计算科学学院，安徽 安庆 246133)



线性齐次型上的周期作用

孙 广 人

(安庆师范大学 数学与计算科学学院，安徽 安庆 246133)

对于一个给定的整系数线性齐次型，考虑整数环上一般线性群中一个线性变换对该线性齐次型的系数的作用。特别地，由定义在数字半群上的线性齐次型的角度出发给出了一个充分条件，如果一般线性群中一个有限周期线性变换满足该条件则存在一个与之共轭线性变换，使得该共轭线性变换生成的循环群作用于一个容许型后所得一族型都是容许型。此外，还给出了一般线性群中一个线性变换相对某个型是有限周期作用的充要条件。

型；周期作用；一般线性群；数字半群

令N是非负整数集合对通常整数加法形成的含幺半群，一个数字半群S是N的含幺子半群，并且它的余集G(S)∶=NS是有限集。

Arf半群是数字半群中较为著名的一种类型，它的定义为对于任意的s1≥s2≥s3∈S，s1+s2-s3∈S，即对于线性齐次多项式p=x1+x2-x3，以及任意的s1≥s2≥s3∈S，有p(s1,s2,s3)=s1+s2-s3∈S。在Arf半群的基础上，Bras-Amorós等[1]引入了数字半群容许线性齐次型的概念：

(1) 存在数字半群容许p；

(2) N容许p；

文献[2]进一步引入了n次对称群Sn的一个子集H对型中系数下标的作用后所得型的集合：

数字半群S称为容许pH当且仅当S容许每个pσ。pH称为一族容许型，如果存在数字半群容许pH。特别地，把p的系数划分为集合A∶={i∶ai≥0}及其余集B∶={j∶aj<0}，这里只考虑满足条件σ(A)⊆A的某些置换σ组成的子群，给出在这些子群的作用下所得一切新pσ都是容许型的充要条件。

以下令e1,…,en为有理数域上n维向量空间V的一组固定标准正交基，并且令GL(n,Q)为全体满足如下条件的线性变换：在e1,…,en下的矩阵为有理数矩阵并且行列式不等于0；GL(n,Z)为GL(n,Q)的子群，包含如下全体线性变换：它们在e1,…,en下的矩阵是整数矩阵，并且行列式等于±1。此时，对σ∈Sn可以定义线性变换：

pH∶={pA∶A∈H}，

数字半群S称为容许pH当且仅当S容许每个pA。pH称为一族容许型，如果存在数字半群容许pH。

引入线性变换带来新的困难是很难保证在线性变换下非负的系数仍然映成非负系数，因此定理1中条件(3)一般较难判断。因此，一个自然的想法是取定一个型p，然后适当分类线性变换对它的作用。本文的工作是选择一类A，使得对于循环群〈A〉，p〈A〉中型的系数周期变化。

1　容许型与有限周期的作用

由于对称群Sn中每个元的周期有限，因此任意置换σ生成循环群〈σ〉作用于型p后所得型的集合p〈σ〉中型的系数呈现周期变化，故相对容易判断p〈σ〉中型是否为容许型。对于GL(n,Z)中一个线性变换A，下面说明在某些条件下，虽然p〈A〉可能不是容许的，但是可以在GL(n,Z)中找到一个与A在GL(n,Q)共轭的线性变换B，使得p〈B〉是容许的。

引理1令A是GL(n,Z)中一个线性变换，其特征多项式为xn-1，则A有分量都是有理数的循环向量α，即α,Aα,…,An-1α是V的一组基。

证明显然xn-1没有重根，但A的极小多项式在复数域中根除重数外与特征多项式的根一样[3]，故xn-1就是A的极小多项式，A在有理数域上有循环向量α=(a1,…,an)T。

例1取任意奇素数l，ζl是复数域上l次本原单位根。熟知扩域Q(ζl)/Q是l-1次循环扩域。取Galois群Gal[Q(ζl)/Q]的生成元σ，显然把Q(ζl)看成Q上l-1维线性空间，σ作为Q(ζl)的线性变换，ζl是一个循环向量。

命题1令A是GL(n,Z)中一个线性变换，V可以分解为A-不变子空间的直和：

V=W1⊕…⊕Wm，

假设A限制于每个Wi上后的线性变换AWi特征多项式为xki-1，其中ki=dimWi，则

(1)A的周期为k1,…,km的最小公倍数；

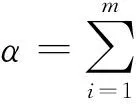
由引理1，设αi是Wi的循环向量，则

是V的一组基，设A在该组基下的矩阵为C，由于它的每个元素非0即1，故C(t1,…,tn)T是非负向量。因此令B在e1,…,en下的矩阵是B=L-1CL，注意到L,C是行列式等于±1整数矩阵，A是有限周期的，可知p〈B〉是容许的，因此(2)成立。

推论1对于任意的σ∈Sn都在GL(n,Z)中存在一个与σ在GL(n,Q)共轭的线性变换B，使得p〈B〉是容许的。

证明σ是恒等置换(1)时结论平凡。假设σ≠(1)，分解为m个不相交的轮换之积：

σ=(i1,1,…,i1,k1)…(im,1,…,im,km)。

令Wj是向量eij,1,…,eij,kj张成的子空间，则σ限制于每个Wj上后的线性变换为周期kj的轮换，特征多项式xkj-1，其中kj=dimWj。因此由命题1知结论成立。

2　范和相对型的有限周期作用

如果A是GL(n,Z)中一个线性变换，但不是有限周期的，仍然有可能存在非零向量α使得向量序列…,A-1α,α,Aα,A2α,…呈现有限周期变化，因此本节不再限制A是有限周期的线性变换。

定义3任意m×n复数矩阵A=(aij)的范‖A‖定义为一切模|aij|中的最大值。

定义4令线性变换A∈GL(n,Q)在e1,…,en下的矩阵为A，称A为一个有界线性变换，如果循环群〈A〉中矩阵的范有界。令非零向量α在e1,…,en下的坐标矩阵为(a1,…,an)T，称A为一个相对α的有界线性变换当且仅当循环群〈A〉作用在α上所得向量序列

…,A-1α,α,Aα,A2α,…

的范有界。

注1显然上述定义与基的选取无关。

注2以下记特征值等于λ的n阶Jordan块矩阵为Jn(λ)=(aij)，即对于所有1≤i≤n，aii=λ，而1≤i≤n-1，aii+1=1，其他aij=0。

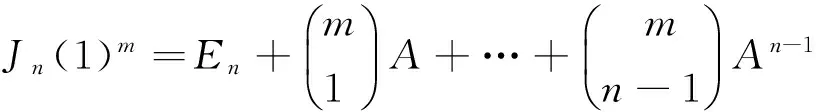
因此线性变换J无界。但是取向量α满足在e1,…,en下的坐标矩阵是(1,0,…,0)T，显然α是J的特征向量，J仅有特征值1，因此J是相对α的有界线性变换。

定义5线性变换A∈GL(n,Q)称为相对非零向量α为有限周期的，如果A限制在α生成的A-循环子空间上的线性变换Aα是有限周期的。

很明显的有

引理2如果线性变换A∈GL(n,Q)相对非零向量α为有限周期的，则A是一个相对α的有界线性变换。

命题2令A是GL(n,Z)中一个线性变换，在e1,…,en下的矩阵是A，非零向量α在e1,…,en下的坐标矩阵是整数矩阵(a1,…,an)T，则A为相对非零向量α为有限周期的当且仅当α存在分解

α=∑αλ，

其中αλ为A的复特征值λ的复特征向量，且λ是单位根。

证明充分性显然，因此只需证明必要性。假设f1,…,fn是A的Jordan基，即A在该组基下的矩阵是Jordan标准形：

diag=[Jk1(λ1),…,Jkm(λm)]

其中λi是A的第i个特征值，ki是Jordan块矩阵Jki(λi)的阶，当A限制在以fi,1,…,fi,ki为基的子空间Wi上的矩阵表示为Jki(λi)。

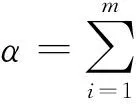
(1)

(2)

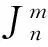
注3|λ|=1且λ是代数整数一般不蕴含λ是单位根[4]。

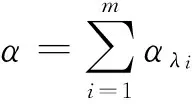
证明由引理2，只需证明充分性。由命题2，αλi≠0必然有|λi|=1，而由已知条件知其所有共轭|σ(λi)|=1，因此由代数数论的知识知λi是单位根，故由命题2即得。

3　问题与发展

本文只是初步探讨了p〈A〉中型的系数周期变化的问题。结合命题1及推论1容易得知前面讨论的线性变换都共轭于Sn中某个置换。在第2部分中虽然给出了型系数在循环群〈A〉作用下周期变化的条件，但是如果p是容许型，本文没有给出相对有限周期的线性变换满足什么条件时能够确保p〈A〉中的型都是容许型。因此，引入更多工具来深入的探讨这些问题是值得期待的。

[1]Bras-AmorósM,García-SánchezPA.Patternsonnumericalsemigroups[J].LinearAlgebraAppl, 2006, 414(2/3): 652-669.

[2] 孙广人. 二分系数作用下的线性齐次型[J]. 安庆师范学院学报(自然科学版)，2014, 20(3): 7-9.

[3]HoffmanK,KunzeR.LinearAlgebra(影印版)[M]. 北京: 世界图书出版公司, 2008: 160-173.

[4]MacCluerCR,ParryCJ.Unitsofmodulus1[J].JNumberTheory, 1975, 7 (4): 371-375.

Periodic Acts on a Linear Homogeneous Pattern

SUN Guang-ren

(Department of Mathematics, Anqing Normal University, Anqing, Anhui 246133，China)

For a linear homogeneous pattern, linear transformations in the general group over integers act on its coefficients are considered. From the view of patterns on numerical semigroups, a sufficient condition is given: under the condition, an element of finite period in the general group has a conjugation, such that the resulted patterns remain admissible by the conjugation generated cyclic subgroup acting on an admissible pattern. Moreover, an equivalent condition for an element in the general group that is finitely periodic relative to a pattern is obtained.

pattern; periodic act; general linear group; numerical semigroup

2016-02-28

孙广人，男，河北唐山人，博士，安庆师范大学数学与计算科学学院副教授，研究方向为代数编码。E-mail: 34900959@qq.com

时间：2016-8-17 11:31

http://www.cnki.net/kcms/detail/34.1150.N.20160817.1131.005.html

G47

A

1007-4260(2016)03-0015-03

10.13757/j.cnki.cn34-1150/n.2016.03.005