带有非线性免疫率的 SIRS 计算机病毒传播模型
昂蓉蓉, 叶 雷
(安徽师范大学 数学计算科学学院,安徽 芜湖 241002)
带有非线性免疫率的 SIRS 计算机病毒传播模型
昂蓉蓉, 叶雷
(安徽师范大学 数学计算科学学院,安徽 芜湖 241002)
本文提出了一类带有非线性免疫率的 SIRS 计算机病毒传播模型,考虑部分易感染类节点,在未被感染的情况下,被新免疫直接免疫后成为免疫状态类节点;同时也考虑部分被免疫后的免疫类节点,在丧失免疫力后又成为易感染类节点。通过计算定义了模型的基本再生数R0,利用LaSalle 不变集原理,构造合适的 Lyapunov 函数,分析计算机病毒在传播过程中的无病毒平衡点和病毒存在平衡点的稳定性,该结果推广了已有文献的结论。
计算机病毒;全局稳定;Lyapunov 函数;数值模拟
计算机病毒通常是一类具有传染性的恶意计算机代码,它是现今网络犯罪中最重要的手段之一。它们是Internet上具有最强破坏性的武器,有可能导致军事、经济、科技、商业等面临巨大的灾难,严重影响人们的日常生活[1]。常见的计算机病毒有:病毒[2]、蠕虫[3]、特洛伊木马[4]、逻辑炸弹等等。目前,人们主要运用微观模型和宏观模型来研究计算机病毒的传播特性。微观模型是从病毒自身出发建立识别病毒的模型,它主要用于研发反病毒软件[5];宏观模型是由 Kephart 等人首次提出[6],其思想是借助于生物传染病的仓室模型,建立计算机病毒的传播仓室模型,研究各仓室内病毒的数量随着时间的变化规律[7],通过预测病毒的演化趋势,从而找到能够有效控制病毒在网络上的传播方法[8]。目前国内外有大量的文献对计算机病毒在网络中的传播过程进行研究分析[9-12],其中Gan[12]提出了一个如下的SIRS模型:
(1)
本文在此基础上,从宏观角度对计算机病毒的传播进行研究,提出一种更好的带有非线性免疫概率的SIRS计算机病毒传播模型。
1 模型的建立
网络可以用若干节点和边来表示,即网络可以看成是由节点和边相互连接构成的图。网络中一台服务器或PC机可以抽象成节点,边则表示两台设备之间的物理连接。某一时刻,网络中的节点可能处于以下3种状态之一[13-15]:
(1) 易感染状态 S(Susceptible):指t时刻尚未被感染但具有被感染风险的节点,记为S(t);
(2) 感染状态 I(Infected):指t时刻已感染病毒的节点,且具有感染可能处于S状态的节点,记为I(t);
(3) 免疫状态 R(Removed):指t时刻对病毒具有免疫功能的节点,记为R(t)。
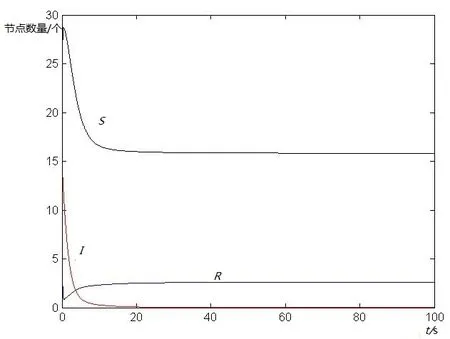
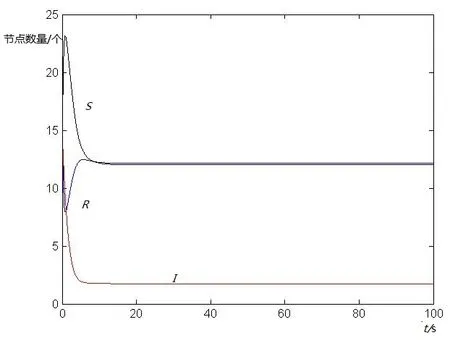
在(1)式中,由于计算机网络处于动态变化之中,应考虑系统存在常数输入率b,将输入节点分为易感染状态类S和免疫状态类 R, 0 根据以上所述,在模型(1)的基础上,建立如下非线性动力学演化方程组: (2) 以N=N(t)表示t时刻此网络中节点的总数量,则N(t)=S(t)+I(t)+R(t)。由系统(2)知N′(t)=b-μ1S-μ2I-μ3R。令μ=min{μ1,μ2,μ3},则N′(t)≤b-μN,因此 令S′(t)=I′(t)=R′(t)=0,很明显存在无病平衡点P0(S0,I0,R0),其中 显然当R0≤1时,系统(2)在Ω内仅有唯一无病毒平衡点P0(S0,I0,R0); 当R0>1时,联立 将3个等式相加得 b-μ1S-μ2I-μ3R=0 (3) 由第2个等式可得 (4) 由第3个等式可得 (5) 将(4)式,(5)式代入(3)式可得 所以存在I*>0使得g(I*)=0。又因为g(I)是一个单调递减的函数,则零点唯一。系统(2)在Ω内除了存在无病毒平衡点P0以外,还有病毒存在唯一的有病平衡点P1(S*,I*,R*)。 定理1当R0≤1时,无病毒平衡点P0在Ω内全局渐进稳定。 证明构造Lyapunov函数 V1=|S-S0|+|I-I0|+|R-R0|, α2R-μ1S-[(1-p)b-α1S0+α2R0-μ1S0]}+ sgn(R-R0){[(pb+γ1I+α1f(I)S-μ3R-α2R]- (pb+α1S0-μ3R0-α2R0)}, -μ(|S-S0|+|I-I0|+|R-R0|)=-μV1,其中μ=min{μ1,μ2,μ3}。对上式两边从t0到t进行积分,可得 由可行域Ω知,S,I,R有界,则它们的导数也有界,从而V1一致有界。故由LaSalle不变集原理可知,当R0≤1时,无病毒平衡点P0全局渐进稳定。 定理2当R0>1时,病毒存在有病平衡点P1在Ω内全局渐进稳定。 证明构造Lyapunov函数 V2=|S-S*|+|I-I*|+|R-R*|, α2R-μ1S-[(1-p)b-α1f(I*)S*+ sgn(R-R*){[pb+γ1I+α1f(I)S-μ3R-α2R]- [pb+γ1I*+α1f(I*)S*-μ3R*-α2R*]}, -μ(|S-S*|+|I-I*|+|R-R*|)=-μV2,其中μ=min{μ1,μ2,μ3}。对上式两边从t0到t进行积分,可得 为了验证理论分析的正确性,观察R0≤1和R0>1时,病毒在网络中流行的不同情况: (1)取b=10,β=0.2,α1=0.8,α2=0.2,p=0.9,γ1=γ2=0.2,μ1=0.8,μ2=0.2,μ3=0.5,此时,R0=0.52≤1,模拟结果如图1所示。 图1 无病平衡点示意图 (2)取b=10,β=0.2,α1=0.2,α2=0.5,p=0.5,γ1=γ2=0.2,μ1=0.3,μ2=0.2,μ3=0.5,此时,R0=2.9>1,模拟结果如图2所示。 图2 有病平衡点示意图 图1表明,当R0≤1时,网络中的病毒数会得到有效控制;图2表明,当R0>1时,网络中的病毒不会被灭绝。 本文建立了一个带有非线性免疫概率的SIRS计算机病毒传播模型,在节点进入网络时,提出了预先免疫的措施,通过分析模型的动力学行为,发现模型中病毒的传播主要依赖于病毒传播的基本再生数R0。当R0≤1时,可以使网络获得全局稳定性,并能最终消除病毒;当R0>1时,处于感染状态的节点会越来越多,最终病毒将一直存在,成为地方病。 [1] Wierman J C, Marchette D J. Modeling computer virus prevalence with a susceptible-infected-susceptible model with reintroduction[J]. Computational Statistics and Data Analysis, 2004, 45(1): 3-23. [2] Han X, Tan Q. Dynamical behavior of computer virus on internet[J]. Applied Mathematics and Computation, 2010, 217(6): 2520-2526. [3] Mishra B K, Pandey S K. Fuzzy epidemic model for the transmission of worms in computer network[J]. Nonlinear Analysis,Real World Applications, 2010, 11(5): 4335-4341. [4] Clark J, Leblanc S, Knight S. Compromise through usb-based hardware trojan horse device[J]. Future Generation Computer Systems, 2011, 27(5): 555-563. [5] 马洪江, 王建忠, 张萍. 基于免疫机制的蠕虫检测防御系统[J]. 重庆师范大学学报(自然科学版), 2005, 23(3): 1-4. [6] Kephart J Q, White S R. Directed graph epidemical model of computer viruses[C]. Proceedings of the 1991 IEEE Symposium on Security and Privacy, Washington DC: IEEE Computer Society, 1991:343-359. [7] 马知恩, 周义仓. 传染病动力学的数学建模与研究[M]. 北京:科学出版社, 2004:3-14. [8] 张宁, 张丹荣, 杨建民. 有限资源下网络病毒的阻断策略[J]. 上海理工大学学报(自然科学版), 2007, 29(3):250-254. [9] 刘铭, 洪帆, 韩兰胜. 一种计算机病毒传播模型的分析与仿真[J]. 计算机仿真, 2010, 27(5):305-308. [10] 李哲, 封汉颖. 一类改进的计算机病毒传播模型[J]. 微计算机信息, 2008, 24(43):64-66. [11] 李晓丽, 王丽娜. 网络中的计算机病毒传播模型 [J]. 计算机工程, 2005, 31(18):153-155. [12] Gan Chenquan, Yang Xiaofan, Liu Wanping, et al. A propagation model of computer virus with nonlinear vaccination probability[J]. Commun Nonlinear Sci Numer Simulat, 2014, 19:92-100. [13] 韩华, 马爱娜, 赵夏, 等. 具有远程感染机制的SIRS传播模型及仿真[J].武汉理工大学学报, 2010(2):141-145. [14] 周海平, 蔡绍兴, 龙艳. 个体差异对病毒传播效率的影响[J]. 计算机应用研究, 2011, 28(10):3797-3798. [15] 夏承遗, 刘忠信, 陈增强, 等. 复杂网络上带有直接免疫的SIRS类传染模型研究[J]. 控制与决策, 2008,23(4):468-472. Propagation Model of SIRS Computer Virus with Non-Linear Vaccination Probability ANG Rong-rong,YE Lei (School of Mathematics and Computation Science, Anhui Normal University, Wuhu, Anhui 241002, China) A propagation model of SIRS computer virus with non-linear vaccination probability is presented. The model takes into account that, in the case of non-infected, some of the susceptible nodes are becoming immune status category nodes directly after the new immunization. In addition, the model also includes the immune nodes which become lost immunity susceptible nodes again. The article draws the conclusion by ways of using the LaSalle invariance principle, constructing Lyapunov function, analyzing the global stabilities of the virus-free equilibrium and the virus equilibrium. computer virus; global stability; Lyapunov function; simulation analysis 2015-05-26 安徽省高校优秀青年人才基金重点项目(2011SQRL022ZD)。 昂蓉蓉,女,安徽合肥人,安徽师范大学数学计算科学科学学院硕士研究生,研究方向为微分方程理论及应用。E-mail: 184850233@qq.com 时间:2016-8-17 11:31 http://www.cnki.net/kcms/detail/34.1150.N.20160817.1131.004.html O175.1;Q141 A 1007-4260(2016)03-0011-04 10.13757/j.cnki.cn34-1150/n.2016.03.004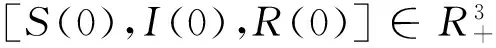
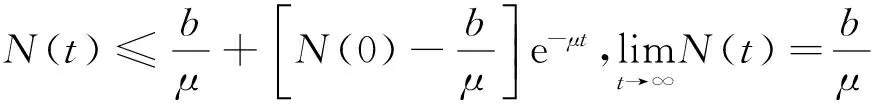
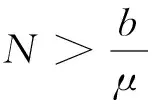
2 平衡点的稳定性分析
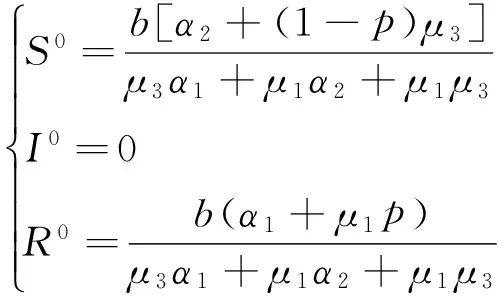
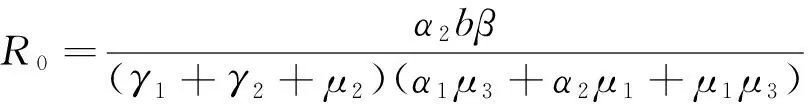
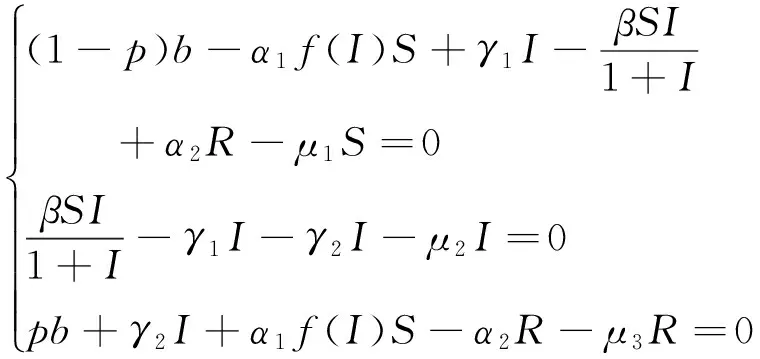
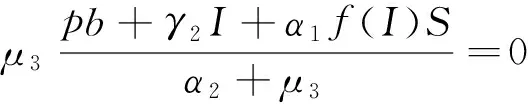
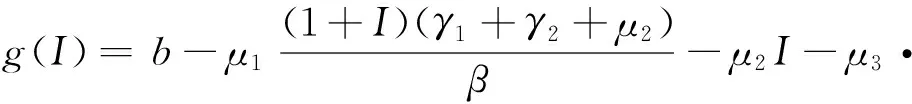
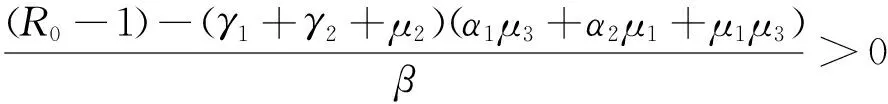
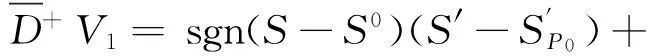
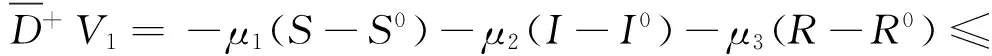
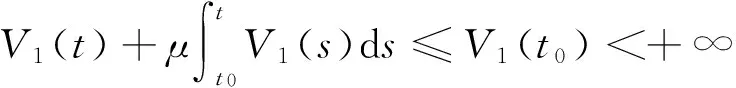
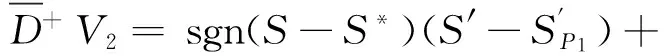
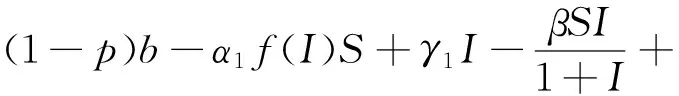
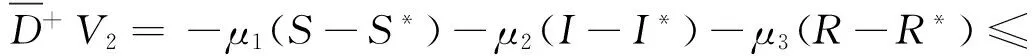
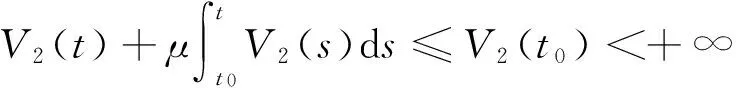
3 模拟仿真
4 结束语

