一类拟变分不等式与Wiener-Hopf方程的等价性及其算法研究

孙 　 杰

(南京财经大学 应用数学学院，江苏 南京 210003)



一类拟变分不等式与Wiener-Hopf方程的等价性及其算法研究

孙 杰

(南京财经大学 应用数学学院，江苏 南京 210003)

在Hilbert空间中研究一类拟变分不等式与Wiener-Hopf方程的等价关系，利用等价关系构建求解这类拟变分不等式的投影迭代算法，并对其收敛性进行分析。

拟变分不等式；Wiener-Hopf方程；算法

设H是Hilbert空间，其内积和范数分别用〈·,·〉，‖·‖表示。拟变分不等式问题QVIP(T,K)最早是由Benousan和Lions[1]介绍的，研究问题为找一点u∈H，使得〈T(u),v-u〉≥0,∀v∈K(u)，其中T∶H→H是一映射，K∶H→2H是集值映射，且对∀u∈H，K(u)是闭凸集。

本文考虑的拟变分不等式问题为找一点u∈H，使得g(u)∈K(u)，且

〈T(u),v-g(u)〉≥0,∀v∈K(u)

(1)

其中T,g∶H→H是连续映射，K∶H→2H是集值映射，且对任意的u∈H，K(u)是闭凸集。上述拟变分不等式问题记为QVIP(T,g,K)。这类拟变分不等式问题由Aussel在2013年提出并研究，可以看作经典拟变分不等式的一个推广。Aussel[2]在Rn空间中假设QVIP(T,g,K)有解的情况下给出了解的误差界，并未涉及解的存在性与算法研究。郭小亚等[3]在Rn空间中讨论了QVIP(T,g,K)解的存在性与算法，并将其运用到交通问题中。本文主要是在Hilbert空间中研究QVIP(T,g,K)与Wiener-Hopf方程的等价关系，利用等价关系构建求解这类拟变分不等式的解的迭代算法，并对算法的收敛性进行分析。

下面先介绍一些概念、引理知识等。

定义1映射T∶H→H是Lipschitz连续的当且仅当存在一个常数β>0，使得

‖T(u)-T(v)‖≤β‖u-v‖，∀u,v∈H。

定义2映射T∶H→H是α-强单调的当且仅当存在一个常数α>0，使得

〈T(u)-T(v),u-v〉≥α‖u-v‖2,∀u,v∈H。

定义3映射T在H上关于g是η-强单调的当且仅当存在一个常数η>0，使得

〈T(u)-T(v),g(u)-g(v)〉≥η‖u-v‖2,∀u,v∈H。

定义4记PK(u)为空间H到K(u)的投影，且令QK(u)=I-PK(u)，其中I为恒等映射，如果g-1存在，求z∈H使得

Tg-1PK(u)z+ρ-1QK(u)z=0

(2)

称形如(2)式的这类方程为Wiener-Hopf方程。

引理1设K(u)是H中的一个闭凸集，对于给定z∈H,u∈K(u)，不等式〈u-z,v-u〉≥0,∀v∈k(u)成立当且仅当u=PK(u)z。

注1这里的投影算子PK(u)是非扩张的，即‖PK(u)x-PK(u)y‖≤‖x-y‖,∀x,y∈H。

假设1[4]对于任意给定的u,v,w∈H，投影算子PK(u)满足‖PK(u)w-PK(v)w‖≤γ‖u-v‖,这里的γ>0是一个正常数。

下面给出Wiener-Hopf方程与QVIP(T,g,K)的等价性及其算法。

定理1若u∈H,g(u)∈K(u)是QVIP(T,g,K)的解当且仅当Wiener-Hopf方程存在解z∈H，

z=g(u)-ρT(u)

g(u)=PK(u)z

(3)

其中PK(u)为空间H到闭凸集PK(u)的投影，且常数ρ>0。

注2这里假设映射g可逆，g-1为g的逆映射。

证明令u∈H，使得g(u)∈K(u)为拟变分不等式(1)的解。由引理1可得

g(u)=PK(u)[g(u)-ρT(u)]，

QK(u)[g(u)-ρT(u)]=g(u)-ρT(u)-PK(u)[g(u)-ρT(u)]=-ρT(u)=

-ρTg-1PK(u)[g(u)-ρT(u)]，

若z=g(u)-ρT(u)，则可得Tg-1PK(u)z+ρ-1QK(u)z=0。

相反，令z∈H为Wiener-Hopf方程(2)的解，则

ρTg-1PK(u)z=-QK(u)z=

-[I-PK(u)]z=PK(u)z-z

DWD无线随钻测量仪器由地面部分、井下部分及辅助工具、设备组成，其工作原理是利用仪器内的涡轮发电机将部分钻井液的能量转化成电能为探管供电，同时钻井液脉冲发生器将探管探测到的数据通过钻井液传递到地面，地面上采用钻井液压力传感器检测来自井下仪器的钻井液脉冲信息，并传输到地面解码箱进行处理，最终井下仪器所测量的井斜角、方位角和工具面数据等信息可以显示在计算机或DDU司钻阅读器上。

(4)由(4)式和引理1可得0≤〈PK(u)z-z，v-PK(u)z〉=〈ρTg-1PK(u)z,v-PK(u)z〉，从而可得〈Tg-1PK(u)z,v-PK(u)z〉≥0,∀v∈K(u)成立。因此g(u)=PK(u)z为拟变分不等式(1)的解，并且由(4)式可以得到z=g(u)-ρT(u)。

通过上面的证明，得到求解QVIP(T,g,K)与求解Wiener-Hopf方程是等价的，因此对Wiener-Hopf方程进行变形，可以得到几个求解QVIP(T,g,K)的迭代算法。

(a)记(2)式中的Wiener-Hopf方程移项变形为QK(u)z=-ρTg-1PK(u)z，将 (3) 式及QK(u)=I-PK(u)代入上式，可到z=PK(u)-ρTg-1PK(u)z=g(u)-ρT(u)，由此可得迭代算法1。

算法1对已知的z0∈H，由如下迭代式计算zn+1，

(5)

(b)记(2)式中的Wiener-Hopf方程移项变形为Tg-1PK(u)z=-ρ-1QK(u)z，两端同时加上QK(u)z得QK(u)z+Tg-1PK(u)z=-ρ-1QK(u)z+QK(u)z。又由QK(u)=I-PK(u)得，

z-PK(u)z+ρTg-1PK(u)z=(1-ρ-1)QK(u)z，

即z=PK(u)z-ρTg-1PK(u)z+(1-ρ-1)QK(u)z=

u-ρT(u)+(1-ρ-1)QK(u)z，结合(3)式得算法2。

算法2对已知的z0∈H，由如下迭代式计算zn+1，

(c)如果T是一个线性可逆映射，则Wiener-Hopf方程(2)式由关系式QK(u)=I-PK(u)可得Tg-1z[I-QK(u)]z+ρ-1=0，对该式进行整理：

Tg-1z-Tg-1QK(u)z+ρ-1QK(u)z=0,

Tg-1z=(Tg-1+ρ-1)QK(u)z,

T(z)=(T+ρ-1g)QK(u)z,

最终得到

z=(I-ρ-1gT-1)QK(u)z。

算法3对已知的z0∈H，由如下迭代式计算zn+1，

zn+1=(I-ρ-1gT-1)QK(un)zn，ρ>0。

注3若K(u)=K，则算法1、算法2、算法3退化为广义变分不等式投影迭代算法(收敛性证明参见文献[5])

若g=I，则算法1、算法2、算法3退化为经典拟变分不等式的投影迭代算法。(收敛性证明参见文献[6-7])

以下将在一定条件下证明算法1的收敛性，同理可证算法2、算法3的收敛性。

定理2T∶H→H关于g是η-强单调且是β-Lipschitz连续的，g∶H→H可逆且是σ-强单调和δ-Lipschitz连续的，若假设1成立并且存在一个常数ρ>0使得

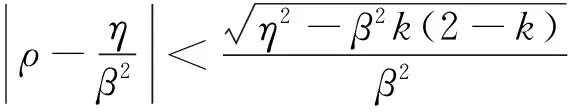
(6)

证明令u∈K(u)是拟变分不等式(1)的解，那么由定理1得到

(7)

因此结合(5) 式得‖zn+1-z‖≤(1-αn)‖zn-z‖+αn‖g(un)-g(u)-ρ[T(un)-T(u)]‖。

由T在H上关于g是η-强单调的且是β-Lipschitz连续的，g是δ-Lipschitz连续的，得到

‖g(u1)-g(u2)-ρ[T(u1)-T(u2)]‖2≤

‖g(u1)-g(u2)‖2+ρ2‖T(u1)-T(u2)‖2-

2ρ〈T(u1)-T(u2),g(u1)-g(u2)〉≤δ2‖u1-u2‖2+ρ2β2‖u1-u2‖2-2ρη‖u1-u2‖2=(δ2+ρ2β2-2ρη)‖u1-u2‖2，

由(5)式，(7)式及假设1，同时g是σ-强单调和δ-Lipschitz连续的，可得‖un-u‖≤‖un-u-[g(un)-g(u)]‖+

‖PK(un)zn-PK(u)z‖≤‖un-u-[g(un)-g(u)]‖+

‖PK(un)zn-PK(un)z‖+‖PK(un)z-PK(u)z‖≤

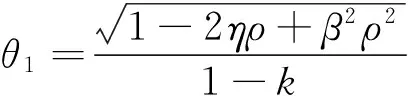
θ1<1，因此 ‖zn+1-z‖≤(1-αn)‖zn-z‖+αnθ1‖zn-z‖≤

[1-(1-θ1)αn]‖zn-z‖≤

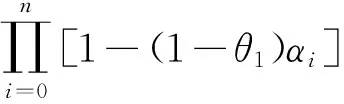
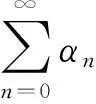
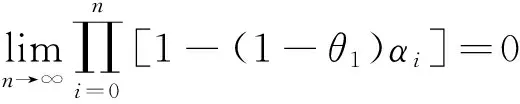
因此{zn}强收敛于z。

[1] Bensousan A, Lions J. Applications Des Inequations Variationelles En Controle Stochastique[M]. Paris:Dunod, 1978.

[2] Aussel D, Gupta R, Mehra A. Gap funtions and error bounds for inverse quasi-variational inequalities problems[J]. Journal of Mathematical Analysis and Applications, 2013, 407(2): 734-748.

[3] Guo Xiaoya, Zhang Congjun. Some reaearch on the quasi-variational inequality and its application in traffic[J]. Mathematica Applicata, 2015, 28(4): 743-752.

[4] Noor M A. On general quasi-variational inequalities [J]. Journal of King Saud University-Science, 2012, 24(1): 81-88.

[5] Noor M A. Differentiable nonconvex functions and general variational inequalities [J]. Applied Mathematics and Computation, 2008, 199(2): 623-630.

[6] Noor M A. Some recent advances in variational inequalities[J]. New Zeal J Math,1997, 26(1): 53-80.

[7] Noor M A. Generalized multivalued quasi-variational inequalities[J]. Computers and Mathematics with Applications, 1996, 31(12): 1-13.

Some Research of the Equivalence with Wiener-Hopf Equations and the Algorithm on a Class of Quasi-variational Inequality

SUN Jie

(School of Applied Mathematics, Nanjing University of Finance & Economics, Nanjing, Jiangsu 210003, China)

In this paper, we establish the equivalence between a class of the Quasi-variational inequality and the Wiener-Hopf equations in Hilbert space. Then we use the equivalence to construct the algorithms for this Quasi-variational inequality, and give convergence analysis.

Quasi-variational inequality; Wiener-Hopf equations; algorithms

2015-12-30

孙杰，男，江苏淮安人，南京财经大学应用数学学院硕士研究生，研究方向为非线性分析与经济应用。E-mail：304978554@qq.com

时间：2016-8-17 11:31

http://www.cnki.net/kcms/detail/34.1150.N.20160817.1131.003.html

O178

A

1007-4260(2016)03-0008-03

10.13757/j.cnki.cn34-1150/n.2016.03.003