二维束宽恒定的二阶锥规划波束形成方法*

张 勇，何培宇，罗胡琴

（四川大学电子信息学院，成都　610065）

二维束宽恒定的二阶锥规划波束形成方法*

张 勇，何培宇**，罗胡琴

（四川大学电子信息学院，成都610065）

二阶锥规划作为凸优化理论的一个分支，近些年来已应用于波束形成的研究，但在已有研究中基于均匀线阵的一维波束形成研究得较多，且较少考虑不同指向下的束宽恒定问题。因此，基于矩形平面阵，将二阶锥规划的一维束宽恒定波束形成方法扩展到二维作为主要研究目标，首先采用Dolph-Chebyshev加权方法设计出二维参考波束，再以主瓣逼近和旁瓣最小为约束，引入二阶锥规划方法设计了支持不同俯仰角和方位角指向的二维波束。经仿真分析，所提方法可实现在三维空间中的不同指向下的波束形成，且在俯仰角设定后，在不同方位指向下可实现3 dB束宽较恒定的波束，减少了指向对波束特性的影响，方便于应用。

阵列信号处理；波束形成；矩形阵列；二阶锥规划；束宽恒定；二维波束

1　引言

基于阵列的波束形成是阵列信号处理的一个重要研究方向。波束形成广泛应用于无线通信、声纳、雷达等领域。为了实现基于传感器阵列的波束形成，需要对各传感器收发信号进行系数加权，从而才能得到期望的方向图，可称为波束图综合。而这些加权系数的求取，涉及到了不同算法的研究。

对于均匀直线阵列，可以将阵列波束图表示成多项式形式，道尔夫利用切比雪夫（Dolph-Chebyshev）函数来表示该多项式，从而提出了经典的切比雪夫波束综合方法［1］。切比雪夫阵列给出了在相同副瓣电平和相同阵列长度条件下的最窄主瓣宽度，但是当阵元个数较大时，切比雪夫阵列激励幅度将在边缘阵元发生突变，不利于馈电。泰勒阵列很好地克服了这个缺点，并能提高天线阵列方向性［2］。而由于很多方向综合问题都可以表示为凸函数优化问题，且与随机优化算法不同的是，凸优化方法可以快速地找到目标函数的最优解。1997年，Lebret和Boyd首先系统地将凸优化算法应用到阵列方向图综合中［3］。而二阶锥规划（Second-Order Cone Programming，SOCP）是凸规划问题的一个子集，可以处理特殊的优化问题。文献［4］较早地将二阶锥规划应用于波束成形中，在进行自适应的波束成形方法的研究中，推导出了其波束形成器的基于二阶锥规划的公式化表达。文献［5-7］则利用二阶锥规划方法的特点，将其应用于提高波束成形的稳健性。

由于传感器阵列的特性，可以方便地对波束进行指向的设定，对基于线阵的常规一维波束形成，当波束指向逐渐偏离基阵法线方向时，主瓣逐渐变宽［8］，这势必导致阵列分辨性能下降。文献［9］提出了基于二阶锥约束的方向不变恒定束宽波束形成方法，但它仅针对一维线阵从而实现的是一维波束形成。本文采用Dolph-Chebyshev加权方法实现了三维空间期望波束，并采用二阶锥规划优化方法，实现了基于矩形平面阵的二维恒定束宽波束形成。

2　参考波束的设计

图1所示的矩形传感器阵列为均匀分布的平面阵。设波束指向为K，阵元间隔为窄带信号中心频率波长的1/2，即dx=dy=λ/2，其中λ为信号波长，每行和每列的阵元数均设为M。

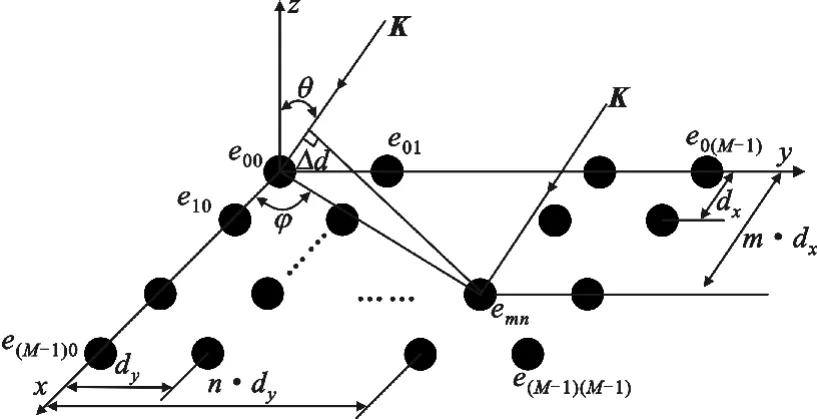
图1　M×M矩形阵列示意图Fig.1 Illustration of M×M rectangular array

波束指向K由方位角φ和俯仰角θ这两个参数确定。根据阵列的几何关系，可以得第m行、第n列的阵元对应的导向系数amn可表达为

当dx=dy=λ/2时，式（1）又可以写为

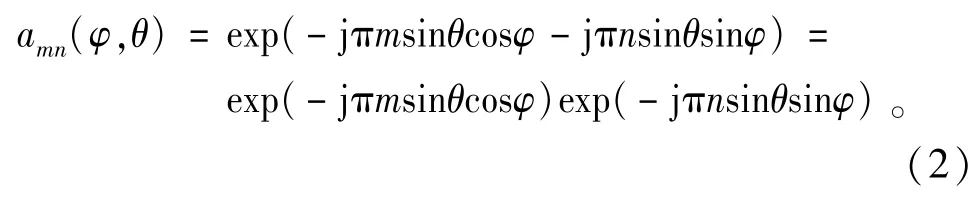
为了实现在不同方位指向上的波束具有恒定的束宽，首先需要设计一个参考波束。本文采用Dolph-Chebyshev加权方法设计该参考二维波束响应。Dolph-Chebyshev加权方法的特点是在给定旁瓣高度的要求下获得最窄的主瓣，或者在给定主瓣宽度要求下获得最低的旁瓣。基于均匀线阵，Dolph-Chebyshev加权方法计算得的第m个阵元对应的加权值为［10，14］

式中：M表示矩形阵的一行所包含的阵元个数；d为阵元间距；λ为信号波长；θNN为波束两零点间束宽的一半；Lsidelobe（单位dB）表示旁瓣水平（由于旁瓣水平比主瓣低，所以用负数表示）。

由式（3）可以看出，所求取到的加权系数wm是对称的。此外，如果直接采用式（3）所求得的加权系数wm对线阵接收信号进行加权求和，接收波束的主轴方向始终指向0°。如果要使波束主轴方向指向其他角度，还需在加权后附加一定的相移。设Dolph-Chebyshev加权矢量wd为

附加一定相移后的加权矢量wx为

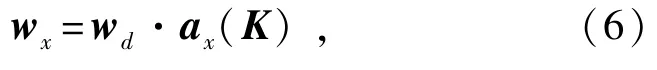
式中：ax（K）为沿x轴的均匀线阵在K方向的阵列导向矢量，而K方向由俯仰角θ和方位角φ确定。另外，式（6）中的两个矢量乘法为点乘，即相应元素对应相乘。同理，可以求得沿y轴的线阵各阵元的加权矢量wy为

根据矩形阵列的几何关系以及式（2），可以推得整个阵列的加权向量为wx和wy的Kronecker积：

式中：w∈CC1×M2，它的每个元素对应于矩形平面阵列的每个阵元的加权系数，而基于这些系数就可得到在设定的俯仰角为θ、方位角为φ时的二维参考波束响应，可表示为

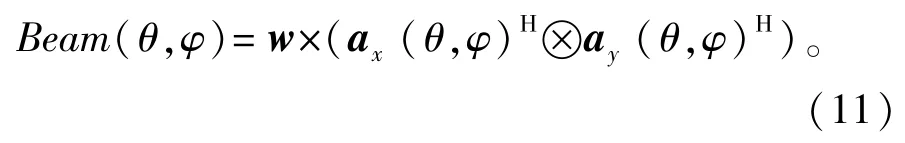
式中：H表示共轭转置。

3　SOCP二维束宽恒定波束形成

在波束形成方面，往往要求不同的波束指向上具备相同的波束特性，这样会对应用上带来更多的方便，如波束指向不影响波束的分辨力。文献［9］提出了基于二阶锥约束的方向不变恒定束宽波束形成方法，但它仅针对一维线阵。而在实际的应用中，往往对二维阵列的恒定束宽波束形成有需求，如希望对三维空间中的某些方向有波束指向要求，这时，就需要波束具备方位和俯仰的指向能力，同时保持束宽的恒定。本文基于矩形平面传感器阵列和二阶锥规划方法，以上一节所产生的Dolph-Chebyshev参考波束为约束，实现了二维恒定束宽的波束形成。借鉴文献［9］思路，并根据本文的三维空间指向波束设计的实际需求，设计准则可描述为

由于式（12）中所涉及到的变量较多，下面对这些变量进行详细解释。w∈CC1×M2为要求取的各阵列加权系数。将感兴趣的三维空间区域用方位角和俯仰角联合表征，设在方位上离散化为N个方位指向，在俯仰上离散化为K个指向，则（ΦiSL，ΘjSL）表示方位和俯仰离散值下标分别为i和j的波束所对应的旁瓣区域，而a（ΦiSL，ΘjSL）则为这些旁瓣区域在所采用的阵列下对应的导向矢量。因此，的物理意义可理解为求取到的权系数w使得当波束指向在感兴趣区域内时，其旁瓣最低。而在这个优化问题下，以为约束条件实现主瓣内的恒定束宽，这里的恒定束宽，指俯仰角设定后，主瓣的方位向和俯仰向的束宽均恒定。（φiq，θjp）为待设计波束的主瓣区域的一种离散化表征，其中的i和j变量含意如前述，该指向下的波束主瓣区域在方位和俯仰上的离散点数分别为P和Q，则Pd（φiq，θjp）为对应于离散点对（q，p）的主瓣响应值（也可理解为该处增益值）。Pr（φ'iq，θ'jp）则对应于参考波束的主瓣区域内离散点对（q，p）的主瓣响应值，而参考波束的主瓣区域在方位和俯仰上的离散点数也分别为P和Q。当每个由变量对（i，j）确定指向的设计波束均采用相同的参考波束时，Pr（φ'iq，θ'jp）也可以写为Pr（φ'q，θ'p）。ε为产生的设计波束与参考波束的主瓣之间允许的误差值。［φL，φ］Ri和［θL，θ］

Rj分别为由（i，j）确定指向的设计波束在方位和俯仰上的主瓣区域。a（φsi，θsj）表示阵列在（i，j）确定的指向上的导向矢量，wHa（φsi，θsj）=1是为了稳健性和归一化的考虑加入的一条约束。

二阶锥规划是一种强有力的优化方法，但在应用这种方法的前提，需将针对实际问题提出的设计约束转化为二阶锥规划的标准形式，如此一些凸优化工具如SeDuMi［11］可以应用。为了便于SeDuMi优化工具计算，式（12）可表示为

式中：δ和εpq都为新引入的非负量；p=1，2，…，P；

式中：｛0｝表示零锥。式（13）的第一个不等式约束可以表示为

式中：R1+表示为非负实数集。借鉴文献［12-13］，式（13）的第二个不等式约束可以表示为

式中：Q3m表示二阶锥；eT（p，q）=［e11，e12，…，ePQ］，且

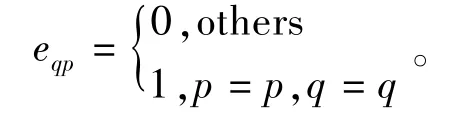
式（13）的第三个不等式约束可以表示为

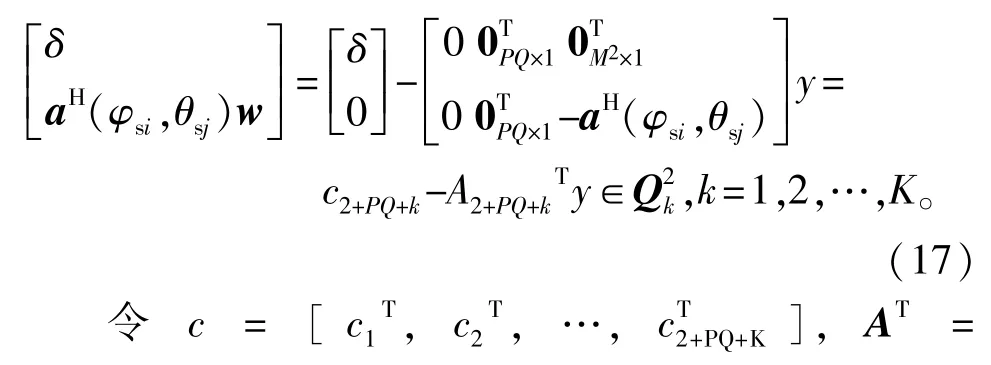
［A1，A2，…，A2+PQ+K］T，则可以方便地利用SeDuMi工具，对于求解问题的转换也可参见文献［14］。

4　仿真与分析

平面阵列为具有15×15阵元的矩形阵，信号中心频率设为900 MHz，相邻阵元之间的间隔为窄带信号中心频率对应波长的1/2；采用Dolph-Chebyshev加权方法设的参考波束的旁瓣设为-40 dB，参考波束指向设为方位角φ=0°，俯仰角θ=20°。

图2显示了参考波束在三维直角坐标系中的波束响应情况，可以看出它在设定的（φ，θ）=（0°，20°）处有明显的高增益波束，其旁瓣均低于设定要求的-40 dB，因此参考波束满足设定要求。

图2　Dolph-Chebyshe加权方法设计的参考波束响应Fig.2 The referential beam designed by Dolph-Chebyshe weighted method

根据本文所采用的基于参考波束的二阶锥规划束宽恒定波束方法，考察设计产生的二维波束的束宽情况。设定俯仰角θ=50°，方位角设为φ=0°～360°时进行考察。图3（a）表示俯仰角为50°指向、不同方位角指向下得到的多个设计波束在俯仰向切面下的波束图，每个波束在方位指向上相隔5°，可见不同方位指向下得到的波束图的主瓣几乎均重合。不同方位的波束，在俯仰向的3 dB束宽均为12°。图3（b）表示为在俯仰角为50°时，变化方位角指向得到的不同设计波束图。可见不同方位角下得到的波束图的方位向切面的主瓣宽度也几乎相同，3 dB束宽均为30°。

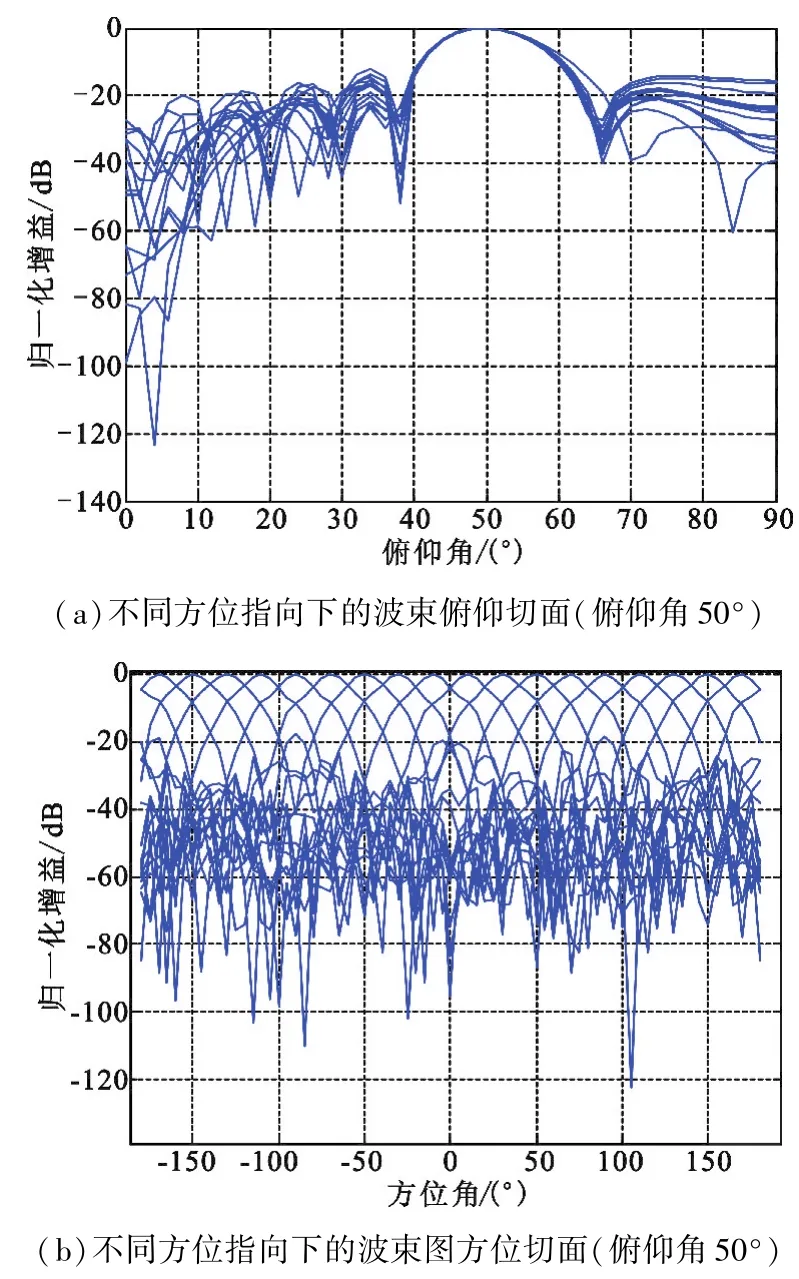
图3　基于SOCP的二维波束恒定束宽响应Fig.3 2D beam SICB response based on SOCP

图4（a）为采用Dolph-Chebyshev加权方法时，方位角为0°，考虑不同俯仰角时实际得到的波束。可见随着俯仰角的增加，在俯仰切面上的波束宽度逐渐增大；当俯仰角达到60°时，已无法形成较完整的波束形态。图4（b）为二阶锥规划束宽恒定方法设计的波束在俯仰角60°时，方位角0°的情况。可见相比Dolph-Chebyshev加权方法，本文的基于二阶锥规划的恒定束宽方法可以较准确地指向设定的俯仰角，且能形成较完整的波束。图4（c）为球坐标下的波束表征，在球坐标下，x-y平面中的x轴为方位角的0°，x-y平面中以原点为起点的矢径长度为俯仰角大小，z轴表征不同方位角和俯仰角下的波束增益大小。

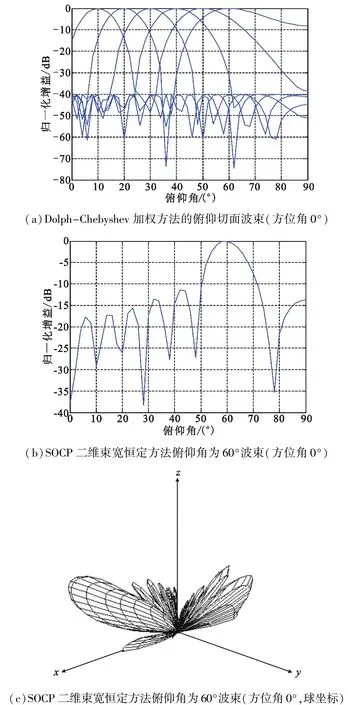
图4　俯仰角对设计波束的影响对比Fig.4 The comparison of different elevation angles

图5为对矩形阵列进行的一次三维空间连续赋形，设定的俯仰角为50°。由于采用恒束宽的波束设计约束，当俯仰角一定，可见在三维空间中的各个方位角上可以得到较均匀的增益赋形。

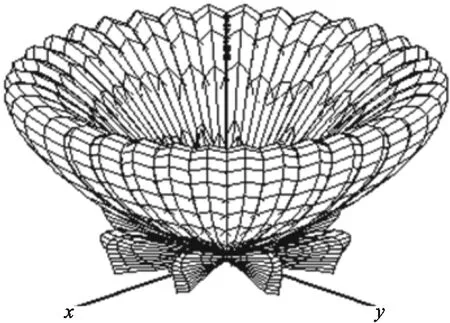
图5　球坐标坐下的阵列波束赋形（俯仰角50°）Fig.5 The continuous forming of beams in spherical coordinate when elevation angle is set as 50°

5　结束语

本文基于矩形平面传感器阵列，采用二阶锥规划（SOCP）方法，以恒定束宽为约束条件，实现了三维空间指向的波束设计，将通常的SOCP一维波束扩展至二维波束。经仿真分析，在俯仰角设定后，在不同的方位指向下得到的波束在方位切面和俯仰切面上其束宽均较恒定；且与Dolph-Chebyshev加权方法相比，所提方法可以适用于更大范围的俯仰角指向。此外，所提方法由于以束宽恒定为设计目标，减少了不同指向下对波束特性的影响，方便于实际应用。下一步的研究方向是将该方法向宽带信号进行扩展。

［1］BELLMAN R.Introduction to matrix analysis［M］.New York：McGrwa Hill，1960.

［2］TAYLOR T T.Design of line source antennas for narrow beamwidth and low side-lobe［J］.IRE Transactions on Antennas and Propagation，1955，3（1）：16-28.

［3］LEBRET H，BOYD S.Antenna array pattern synthesis via convex optimization［J］.IEEE Transactions on Signal Processing，1997，45（3）：526-532.

［4］LIU J，GERSHMAN A B，LUO Z Q，et al.Adaptive beamforming with sidelobe control：a second-order cone programming approach［J］.IEEE Signal Processing Letters，2003，10（11）：331-334.

［5］VOROBYOV S A，GERSHMAN A B，LUO Z Q.Robust adaptive beamforming using worst-case performance opti-mization：a solution to the signal mismatch problem［J］. IEEE Transactions on Signal Processing，2003，51（2）：313-324.

［6］VOROBYOV S A，GERSHMAN A B，LI Z Q，et al.A-daptive beamforming with joint robustness against mismatched signal steering vector and interference nonstationarity［J］.IEEE Signal Processing Letters，2004，11（2）：108-111.

［7］LIAO B，TSUI K M，CHAN S C.Robust beamforming with magnitude response constraints using iterative second-order cone programming［J］.IEEE Transactions on Antennas and Propagation，2011，59（9）：3477-3482.

［8］VAN TREES H L.Optimum array processing［M］.New York：John Wiley&Sons Inc.，2002.

［9］幸高翔，蔡志明.基于二阶锥约束的方向不变恒定束宽波束形成［J］.电子与信息学报，2009，21（9）：2109-2112. XING Gaoxiang，CAI Zhiming.Steering-invariant constant beamwidth beamforming with SOCP constraints［J］. Journal of electronics and information，2009，21（9）：2109-2112.（in Chinese）

［10］DOLPH C L.A current distribution for broadside arrays which optimizes the relationship between beam width and side-lobe level［J］.Proceedings of the IRE，1946，34（6）：335-348.

［11］STURM J F.Using SeDuMi 1.02，a MATLAB toolbox for optimization over symmetric cones［J］.Optimization Methods and Software，1999（11/12）：625-653.

［12］YAN S F.Optimal design of FIR beamformer with frequency invariant patterns［J］.Applied Acoustics，2006，67（6）：511-528.

［13］LIU J，GERSHMAN A B，LUO Z Q，et al.Adaptive beamforming with sidelobe control：a second-order cone programming approach［J］.IEEE Signal Processing Letters，2003，10（11）：331-334.

［14］鄢社锋，马远良.传感器阵列波束优化设计及应用［M］.北京：科学出版社，2009：96-99，287-290. YAN Shefeng，MA Yuanliang.Optimization design and application of beam based on sensor array［M］.Beijing：Science Press，2009：96-99，287-290.（in Chinese）

张 勇（1979—），男，四川荣县人，2003年于四川大学获计算机及应用专业工学学士学位，2007年于四川大学获电路与系统专业理学硕士学位，现为博士研究生、高级工程师，主要研究方向为阵列信号处理、传感器网络及卫星通信等；

ZHANG Yong was born in Rongxian，Sichuan Province，in 1979.He received the B.S.degree and the M.S.degrees from Sichuan University in 2003 and 2007，respectively.He is now a senior engineer and currently working toward the Ph.D.degree.His research concerns array signal processing，sensor networks and satellite communication.

Email：zhangyong5719@163.com

何培宇（1963—），女，四川茂县人，1986年于清华大学无线电电子学系获工学学士学位，1989年于四川大学无线电电子学系获理学硕士学位，2005年于四川大学获通信与信息系统专业工学博士学位，2000～2001年赴荷兰Eindhoven工业大学电气工程系作访问学者，现为教授、博士生导师，现任四川大学电子信息学院无线电技术与信息系统教研室主任及四川大学-德州仪器DSP联合实验室主任，主要研究方向为自适应信号处理及DSP技术、阵列信号处理等；

HE Peiyu was born in Maoxian，Sichuan Province，in 1963. She received the B.S.degree from Tsinghua University，the M. S.degree and the Ph.D.degree from Sichuan University in 1986，1989 and 2005，respectively.She is now a progfessor and also the Ph.D.supervisor.Her research concerns adaptive signal processing，DSP technology and array signal processing.

Email：hepeiyu@scu.edu.cn

罗胡琴（1990—），女，四川邻水人，2015年于四川大学获工学硕士学位，主要研究方向为阵列信号处理。

LUO Huqin was born in Linshui，Sichuan Province，in 1990.She received the M.S.degree from Sichuan University in 2015.Her research concerns array signal processing.

A 2-D Steering-invariant Constant Beamwidth Beamforming Algorithm Based on Second-order Cone Programming Constraints

ZHANG Yong，HE Peiyu，LUO Huqin
（School of Electronics and Information Engineering，Sichuan University，Chengdu 610065，China）

Second-Order Cone Programming（SOCP）is a study branch of convex optimization theory，and has been applied in beamforming field in recent years.Conventionally，the beamforming algorithms based on the SOCP were usually applied on uniform linear array（ULA），and few methods were proposed to consider the steering-invariant constant beamwidth（SICB）.Based on planar rectangle array，this paper expands 1-D SICB beamforming to 2-D.Firstly，the expected beam is designed by employing Dolph-Chebyshev weighted method.Next，SOCP is introduced to design the 2-D beam with the constraints of approaching mainlobe of expected beam and minimizing sidelobes.Computer simulations show that 2-D beamforming can be achieved for 3-D space.As the elevation angle is set，the 3 dB beamwidth can be almost constant even with the different azimuths，which reduces the effect of steering on beam and is benefit to application.

array signal processing；beamforming；planar rectangle array；second-order cone programming；constant beamwidth；2-D beam

TN911.7

A

1001-893X（2016）04-0383-06

10.3969/j.issn.1001-893x.2016.04.006

张勇，何培宇，罗胡琴.二维束宽恒定的二阶锥规划波束形成方法［J］.电讯技术，2016，56（4）：383-388.［ZHANG Yong，HE Peiyu，LUO Huqin.A 2-D steering-invariant constant beamwidth beamforming algorithm based on second-order cone programming constraints［J］. Telecommunication Engineering，2016，56（4）：383-388.］

2015-09-30；

2016-01-07 Received date:2015-09-30；Revised date:2016-01-07

**通信作者:hepeiyu@scu.edu.cn Corresponding author：hepeiyu@scu.edu.cn