基于改进层次分析法的节水灌溉模式优选

李道西, 王一博

(华北水利水电大学 水利学院,河南 郑州 450045)

，

α*=αmin+αmax-α。

。

。

表1 改进后的5/5—9/1比例标度表

。

。

。

，

，

。

表2 平均随机一致性指标RI

表3 方案A、B、C、D的各指标值

表4 经济指标权重评分值

表5 目标层及准则层综合评价值



基于改进层次分析法的节水灌溉模式优选

李道西, 王一博

(华北水利水电大学 水利学院,河南 郑州 450045)

提出了基于改进层次分析法的节水灌溉模式优选方法。以传统层次分析法为理论依据,结合现今人们对事物的认知习惯,对传统层次分析法中1—9比例标度表对人们主观思维的量化原理进行了分析并加以改进,采用更为科学合理的5/5—9/1比例标度表并进行了实例验证。结果表明,改进后的层次分析法所确定的指标权重科学合理,更贴近人们的主观思维,且具有模型简单、便于掌握的优点,可用于节水灌溉模式的优选。

节水灌溉；优选方法；改进层次分析法；比例标度；综合评价

当前不少地区对节水灌溉模式的选择仅凭以往经验进行决断,对节水灌溉模式的前期调查评价不够深入,结果使工程应用后不能发挥预期效益[1]。因此,有必要结合当地的实际情况推算优选出适宜当地经济、技术以及社会等因素的节水灌溉模式。

目前,已有多种节水灌溉模式的优选方法,如模糊综合评价法[2]、集对分析法[3]、灰色关联分析法[4]、主成分分析法[5]、模糊物元分析法[6]、TOPSIS模型法[7]、层次分析法[8-9]等。每种方法各有优劣，如模糊综合评价法的数学模型简单，易于掌握，但不能有效地解决指标间因存在相关关系而造成的信息重复问题；集对分析法把确定性分析和不确定性分析有机地结合起来，但需要从集对的两个集合特性出发进而实现到多个集合的转化，较为复杂；灰色关联分析法能够处理部分信息明确的灰色系统，所需的数据量不是很大，但通过该法定义时间变量的几何曲线则比较困难；主成分分析法可将存在相关关系的多指标化为少数的综合指标，但主成分的含义解释一般带有模糊性；TOPSIS法适用于指标数和对象数较少的系统。本文所采用的层次分析法模拟了人的决策思维过程,将定性分析与定量分析有机结合,并最大限度地消除人的主观影响,适用于定性因素起主导作用的决策问题[10],因此被广泛地应用于节水灌溉模式的优选。

层次分析法在实施过程中的一个关键步骤就是构造判断矩阵计算相对权重,而在构造判断矩阵时,通常使用1—9比例标度表。例如,若指标A较指标B略微重要,那么二者的相对重要性在该表中取3/1,即7.5/2.5,这显然并不十分符合人的主观判断,而取为6/4更容易被人们所接受。本文试图针对这一不足,对传统层次分析法中比例标度表进行改进,使评价过程更加符合人的主观判断,使评价结果更加科学合理。

1 改进层次分析模型的构建

层次分析法是美国数学家T. L. Saaty教授于20世纪70年代初期提出的一种简便、灵活而又实用的多方案优化决策方法。通常的做法是:首先根据目标问题构建具有递阶层次的评价指标体系,并对指标进行规范化和同趋势化处理；然后比较每一层次要素间的相对重要性,利用1—9比例标度表构建判断矩阵;通过计算判断矩阵的最大特征值及其特征向量,得出该层要素的权重;再计算出各层次要素对总体目标的组合权重；最后与各指标进行综合,得出不同设想方案的综合效益指标值,为选择最优方案提供依据。

1.1 评价指标体系的建立

应用文献[7]中的评价指标,将评价指标分为国民经济评价指标、技术评价指标及社会评价指标,构建节水灌溉评价指标体系，如图1所示。该体系包含有定量和定性两类指标。其中,定性指标还需要通过专家打分法进行量化处理。例如,定性指标评语集为:很好、较好、一般、较差、很差,对应的隶属度可设置为:1.00、0.75、0.50、0.25、0.00。

图1 具有递阶层次的节水灌溉评价指标体系

1.2 评价指标的规范化和同趋势化处理

由于评价指标间数量级相差过大且部分指标有量纲，不具有可比性,故而需先将评价指标进行规范化处理[11],将各指标值均转化至区间[0,1]上，其处理方法见式(1)。另外,节水灌溉评价指标体系中有些指标为正向指标,即越大越优;有些指标为逆向指标,即越小越优。对于逆向指标就需要进行同趋势化处理,即将逆向指标正向化,其处理方法见式(2)。

(1)

α*=αmin+αmax-α。

(2)

式中:α*为处理后的指标值;αmax为指标最大值;αmin为指标最小值;α为原指标值。

1.3 构造指标比较判断矩阵

聘请6～10名从事节水灌溉的专家组成专家组,各专家分别对同级指标两两比较,通过比例标度表将定性指标量化,构造各层次判断矩阵A=(aij)n×n。其中,aij表示指标αi对指标αj的相对重要程度,根据传统层次分析法中1—9比例标度表取1、3、5、7、9时,分别对应:同等重要、略微重要、相当重要、明显重要、绝对重要。1—9比例标度给出的标度值是等差递增的,对此标度的合理性,可以通过算例说明。

假设有3个指标,指标k1、k2、k3,指标间存在序关系k1≻k2≻k3,其中k1比k2稍微重要,k2比k3稍微重要,可设m1、m2、m3是相对的重要程度。采用1—9比例标度对指标间的相对重要程度之比赋值,可得

由传递性得

由1—9比例标度的定义,得到k1比k3绝对重要,而在常识中,人们认为k1比k3明显重要才是合理的,显然由1—9比例标度得到的结果与人们的正常判断存在较大偏差。因此,笔者认为1—9比例标度不能准确、客观地反映人们的主观判断。

将5/5—9/1比例标度、9/9—9/1比例标度、9k/9指数标度、ak-1指数标度、1—5比例标度、1—9比例标度等6种标度进行比较[12],结果表明，5/5—9/1比例标度传递性最好,判断矩阵的偏差最小,能够客观、合理地反映人们的主观思维。

据此,可将1—9比例标度表改进为5/5—9/1比例标度表,见表1,从而将同等重要、略微重要、相当重要、明显重要、绝对重要的期望值分别修订为1.00、1.50、2.33、4.00、9.00,修订后的比例标度表更加符合人的主观判断。

表1 改进后的5/5—9/1比例标度表

相对重要性定义说明5/5=1.00同等重要两目标同样重要6/4=1.50略微重要一个比另一个略微重要7/3=2.33相当重要一个比另一个重要8/2=4.00明显重要深感一个比另一个重要9/1=9.00绝对重要明显感到一个比另一个重要得多5.5/4.5,6.5/3.5,7.5/2.5,8.5/1.5两个相邻判断的中间值需要折中时采用

1.4 计算指标权重

1)计算判断矩阵每一行元素的乘积Mi。

(3)

2)计算Mi的n次方根Di。

(4)

3)对特征向量W=(w1,w2,…,wn)做归一化处理,得到处理后的权重值。

(5)

4)通过计算最大特征根λmax、一致性指标CI以及随机一致性比率CR,进行一致性检验。

(6)

(7)

(8)

式中:(AW)i表示AW的第i个分量；RI为平均随机一致性指标,可由表2查得。

表2 平均随机一致性指标RI

阶数n3456789RI0.580.901.121.241.321.411.45

当随机一致性比率CR<0.1时,认为判断矩阵具有满意的一致性,否则应对判断矩阵进行调整。

1.5 计算综合评价值

将各指标权重与对应指标的规范化和同趋势化处理结果相乘并累加求和,即得到准则层的综合评价值。进一步地,将准则层的权重与准则层的综合评价值相乘并累加求和,即得到各方案的最后综合评价值[13]。

2 实例分析

本文以文献[7]为实例参照,针对某地区管道灌溉、喷灌、滴灌和小管出流灌溉4种节水灌溉模式(分别对应方案A、B、C、D),用本文提出的改进层次分析法进行优选,各方案的指标值见表3,依据1.2节式(1)和式(2)将评价指标进行规范化和同趋势化处理。

表3 方案A、B、C、D的各指标值

评价指标方案A方案B方案C方案D定量指标 投资回收期E1/a13.2014.2012.8011.50 收益率E2/%12.8013.5011.2014.20 效益费用比E32.101.941.861.65 净现值E4/万元9.2010.8011.269.60 灌水均匀度T1/%91.6082.4085.2083.20 灌水强度T2/(mm/h)9.108.609.309.20 灌溉水利用率T3/%92958590定性指标 对作物的适应性T4/%9080100100 对地形的适应性T5/%100100100100 施工难易程度T6/%80709080 农民欢迎程度S1/%807010090 安全可靠性S2/%90869282

请专家构造准则层和指标层的判断矩阵,计算其权向量并进行一致性检验。限于篇幅,这里仅给出经济指标判断矩阵的形成，见表4。

表4 经济指标权重评分值

经济指标投资回收期E1收益率E2效益费用比E3净现值E4指标权重 投资回收期E115.5/4.54.5/5.55/50.25 收益率E24.5/5.514.5/5.55.5/4.50.24 效益费用比E35.5/4.55.5/4.516/40.30 净现值E45/54.5/5.54/610.21

依据1.4节的步骤1—4即可计算出经济指标权重向量为

ωe=(0.25,0.24,0.30,0.21)T,

随机一致性比率CR=0.005 7<0.1,满足一致性检验。

同样地,可计算出技术指标、社会指标、准则层的权重向量分别为:

ωt=(0.14,0.12,0.17,0.17,0.18,0.22)T,

ωs=(0.45,0.55)T,

ω=(0.38,0.34,0.28)T。

经计算，均满足一致性检验。进一步地,计算出准则层和目标层的综合评价值并进行总排序,见表5。

表5 目标层及准则层综合评价值

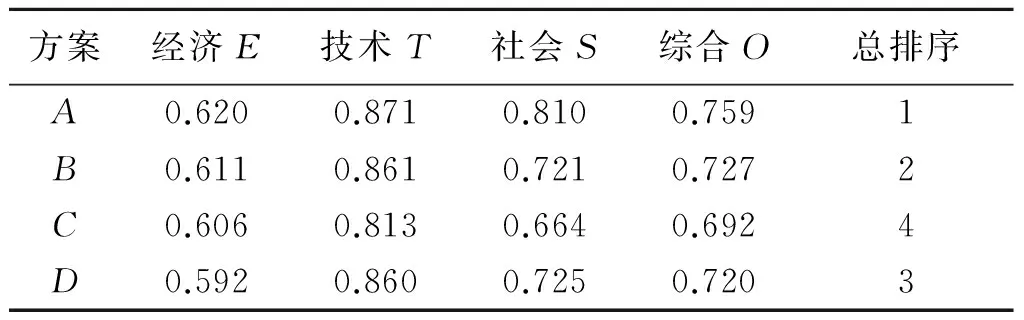
方案经济E技术T社会S综合O总排序A0.6200.8710.8100.7591B0.6110.8610.7210.7272C0.6060.8130.6640.6924D0.5920.8600.7250.7203

计算结果表明,方案A(即管道灌溉)为最佳方案,与文献[7]的评价结果一致。由此说明,基于层次分析原理提出的改进方法所得到的评价结果并未失真,可以为节水灌溉模式的优选提供有效决策。

3 结 语

运用层次分析法确定权重时,由于判断矩阵的给出具有很大的人为主观因素,从而对于权重的确定影响很大,换句话说,使用不同的标度对最后确定的权重值的影响较显著。但根据一致性理论,在建立的判断矩阵满足一致性的前提下,对于具有一定差别的判断矩阵,应用特征值法所求得的权重系数只是各数值大小的不同,并不影响排序。

本文实例中的评价指标的规范化和同趋势化方法与文献[8]也是一致的,所以最终综合评价值的排序也是一致的。如果评价指标的规范化和同趋势化方法发生变化,综合评价值的排序有可能发生变化,还需要进一步研究。

[1]赵林,谭炼,梁炜.基于层次分析模型的节水灌溉优化选择[J].湖南科技学院学报,2011,32(12):16-18.

[2]严乐军.模糊综合评判法在节水灌溉项目投资决策中的应用[J].节水灌溉,2000(4):11-13.

[3]高军省.节水灌溉方案优选的集对分析方法[J].节水灌溉,2010(12):81-83.

[4]罗金耀,李道西.节水灌溉多层次灰色关联综合评价模型研究[J].灌溉排水学报,2003,22(5):38-41.

[5]王爽英,李立辉,戴向洋.基于主成分分析方法的湖南省农业区域经济评价及发展方向[J].农业现代化研究,2010,31(2):241-244.

[6]郭文献,徐建新,卢双宝.模糊物元模型在节水灌溉方式优选中的应用[J].中国农村水利水电,2006(5):27-33.

[7]邓丽娟,马爱玲.基于CRITIC权重与TOPSIS模型的节水灌溉方案优选[J].水科学与工程技术,2010(2):10-12.

[8]张庆华,白玉慧,倪红珍.节水灌溉方式优化选择[J].水利学报,2002,33(1):47-51.

[9]张志政,王敏,苏静.利用层次分析法优化选择节水灌溉方式[J].农机化研究,2008(4):55-58.

[10]刘朝亮.层次分析法在农业系统中的应用研究[J].广东农业科学,2013(13):228-232.

[11]董磊.节水灌溉方式选择中综合评价方法的应用[J].河南水利与南水北调,2012(14):177-178.

[12]郭亚军,张发明,易平涛.标度选择对综合评价结果的影响及合理性分析[J].系统工程与电子技术,2008,30(7):1277-1280.

[13]桑华,李琳.Z地区节水灌溉方式的优化选择[J].华北水利水电学院学报,2009,30(2):34-36.

(责任编辑：陈海涛)

Optimal Selection of Water-saving Irrigation Modes Based on Improved Analytic Hierarchy Process

LI Daoxi, WANG Yibo

(School of Water Conservancy, North China University of Water Resources and Electric Power, Zhengzhou 450045, China)

An optimization method of water-saving irrigation modes based on the improved analytic hierarchy process (IAHP) was proposed in this paper. Taking the traditional AHP as theoretical basis, in view of present people′s cognitive habits, the quantification principle of comparative scale table 1—9 based on the traditional AHP for people′s subject thinking was analyzed and improved, more scientific and reasonable comparative scale table 5/5—9/1 was adopted to testify the IAHP. The results show that the index weight determined by the IAHP was scientific and reasonable, and closer to people′s subject thinking. The IAHP has simple models and is easily grasped, can be used to optimize the modes of water-saving irrigation.

water-saving irrigation; optimization method; improved analytic hierarchy process (IAHP); comparative scale table; comprehensive evaluation

2016-03-03

华北水利水电大学研究生教育创新计划基金(YK2015-03)。

李道西(1978—),男,湖北鄂州人,副教授,硕士生导师,博士,主要从事农业高效节水方面的研究。E-mail:ldx97042@163.com。

王一博(1992—),男,河南郑州人,硕士生,主要从事节水灌溉方面的研究。E-mail:1006639280@qq.com。

10.3969/j.issn.1002-5634.2016.03.004

TV93;S274.3

A

1002-5634(2016)03-0023-04