基于二进制序列索引的灰色马尔科夫交通流量预测模型

尹素素，严　凌

（上海理工大学管理学院，上海 200093）

基于二进制序列索引的灰色马尔科夫交通流量预测模型

尹素素，严凌

（上海理工大学管理学院，上海 200093）

针对短时交通流量预测在精度和收敛速度方面的不足，将二进制序列索引和灰色马尔科夫波动性预测模型相结合，用于短时交通流量预测.通过二进制序列索引，将传统灰色马尔科夫模型中的直接流量数据变为间接流量数据，以减少后期数据处理中误差导致的蝴蝶效应；同时通过波动性数据处理方法的逆方法将预测值还原到索引序列，使灰色马尔科夫预测模型可用于波动性数据的预测，并自主调整预测精度和收敛速度.以松原市兴业大街松原大路交叉口某一进口道的短时交通流量过程为例，对模型进行检验，结果表明：将经过二进制序列索引后的间接交通流量数据运用于优化后的灰色马尔科夫模型后，短时交通流量预测值的相对误差由0.46缩小至0.07，大幅提升了预测数据的精度，说明模型具有良好的预测精度，可以满足短时交通流量预测的要求，具有较高的实用性.

交通工程；交通流量预测；二进制序列；灰色马尔科夫模型

交通流量是指在选定的时间段内通过道路某一地点、某一断面或某一车道的交通实体数.根据交通流量大小可以判定交通的拥挤状况，从而决定采取何种交通管理措施，因此交通流量的准确检测在交通工程中非常重要.但交通流量受城市环境、经济、产业结构、文化和生活习惯等因素的影响，是各种因素通过各种相互关系综合作用的结果［1］，是随机性和规律性的统一.与长期流量预测相比，短时交通流量预测的不确定性更强，受随机干扰因素的影响更大，规律性不明显.目前，国内外针对短时交通流量预测的模型和方法主要有：①基于线性理论的模型和方法，如卡尔曼滤波法［2］；②基于计算机人工智能的预测方法，如神经网络法［3］和非参数回归法［4］等；③基于非线性理论的方法，如小波分析法［5］；④基于组合的预测方法［6-7］；⑤基于交通模拟的预测方法，如元胞自动机［8］和动态交通分配［9］等.所有模型均需要大量历史数据，对于同一算法模型，历史信息交通流量吸收程度与其预测精度通常是正相关的.与以上研究方法不同，灰色系统理论具有所需样本少、无需计算统计特征量等特点.灰色预测是灰色系统理论的重要组成部分，其中应用较为广泛的是传统GM（1，1）模型.灰色马尔科夫模型是一种结合灰色系统理论和马尔科夫链的理论预测模型.灰色预测方法用于预测变化趋势较为明显的时间序列，对随机波动性较大的时间序列效果欠佳，而马尔科夫链的理论适用于随机过程的状态转移行为，可以有效弥补灰色预测的局限.

由于传统GM（1，1）模型仅适用于原始数据序列按指数规律变化且变化速度较慢的情况［10-11］，当时间序列数据不规则波动变化时，数据拟合效果不够理想，本研究拟采用可以弱化原始数据随机性、提高时间序列规律性的波动性数据处理方法解决此问题.此外，原始交通流量数据在不断处理的过程中会出现可容误差，而这些误差会在接下来的一系列计算中产生蝴蝶效应，导致误差变得更为显著，影响预测数据的准确性.本研究采用基于二进制索引的间接流量预测模型对原始交通流量数据进行初处理，以期减少后期数据处理中的蝴蝶效应，对交通流量进行短时预测.

1　建立灰色马尔科夫预测模型

1.1灰色预测模型

根据灰色系统理论，设原始流量数据X（0）（i）=｛x（0）（1），x（0）（2），x（0）（3），…，x（0）（m）｝，通过累加序列（1-AGO）得到一阶累加序列X（1）（i）=｛x（1）（1），x（1）（2），x（1）（3），…，x（1）（m）｝，其中

根据GM（1，1）模型可以求出一次累加生成量X（1）（i）的模型预测值

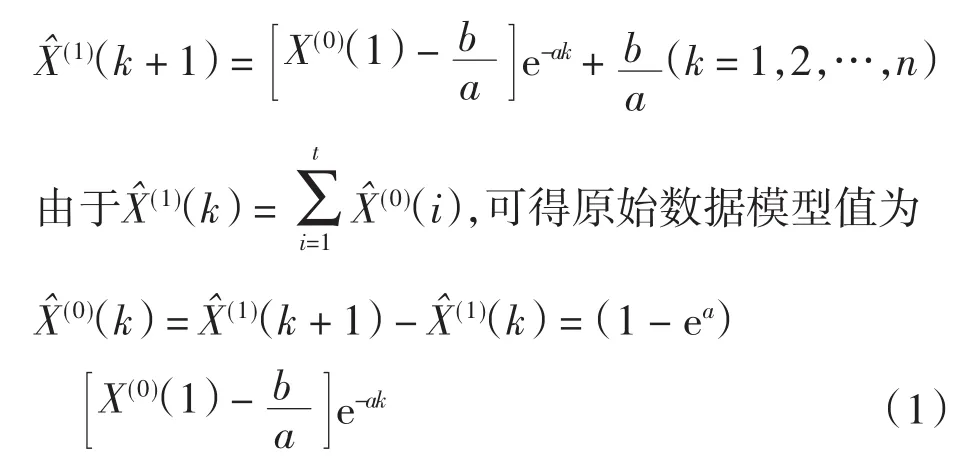
式（1）中：a和b为可标定的参数；e为自然常数2.718.

1.2马尔科夫状态划分和状态转移矩阵

1.2.1状态划分

1.2.2状态转移矩阵

设Λij（n）为状态Θi经n步转移到状态Θj的样本数，ψi为处于状态Θi的样本数，pij（n）为状态Θi到状态Θj的n步转移概率，则pij（n）=Λij（n）/ψi，n步转移概率矩阵

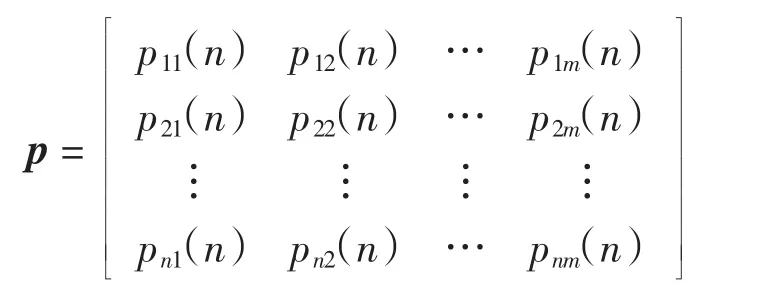
1.2.3确定二进制索引的预测值

确定状态转移矩阵后，通过分析系统现有状态，运用概率加权确定系统特征量的预测值

2　模型优化及二进制序列索引

2.1灰色模型的优化

针对GM（1，1）模型在应用过程中预测精度欠佳的不足对背景值的构造和初始条件的设定进行精度优化.

2.1.1背景值Z（1）（k）的构造

传统GM（1，1）模型误差部分源于背景值的选取［14］，传统模型的背景值由于模型通过梯形面积代替曲边梯形面积，造成预测精度降低.

本研究采用曲边梯形面积构造背景值，背景值Z（1）（k）的优化公式为

式（3）中：x（1）（k）≠x（1）（k-1）.

当x（1）（k）=x（1）（k-1）时，传统背景值Z（1）（k）=；优化后背景值Z（1）（k）=，此结果与传统GM（1，1）模型一致，因此，为减小误差，本研究选取背景值优化计算背景值.

2.1.2初始条件的设定

实际建模中可以在原始数据序列中取出一部分数据进行建模.在利用灰色模型进行预测的过程中，精度较高的只有原点数据X（0）（n）后的1～2个数据［15］.一般情况下，越往未来发展就越远离时间原点，预测价值也随之降低.在实际应用中须不断考虑随时间推移相继进入系统的扰动和驱动因素，随时将每个新得到的数据置入x（0）中，建立信息模型.若以x（1）（n）为初始条件，则，从而信息得到充分利用.

灰色预测模型并不是原始数据越多预测精度就越高，距离时间原点较远的信息对模型预测作用不大，甚至会出现反作用，导致模型精度迅速降低.因此，初始条件的选取应既体现信息优先原理，又体现最佳拟合条件，本研究选取以x（1）（n）为中心的x（1）（n）+δ作为初始条件，运用最小二乘原理，在x（1）（n）+δ内采用一定的步长，计算出总误差最小解作为GM（1，1）的解.

2.2时间序列的二进制索引转化

为描述交通流量的变化，通过建立时间与交通流量的正相关曲线来表示交通流量随时间的变化情况.交通流量的二进制索引转化可以抽象描述交通状态的演变，为了建立二进制索引，研究中将时间-交通流量曲线在横向坐标轴上划分为m段，表示m个时间序列；在纵坐标划分为n段，表示n个交通流量水平，如图1所示.

图1　交通流量水平划分Fig.1　Level division of traffic flow

2.2.1横向时间序列的分段确定

交通流量横向分段由检测器的检测间隔决定，如检测器检测间隔为5 min，则时间序列最小为5 min，也可为5 min的倍数.时间间隔越小所反映的交通流量变化越详细，但也会失去一些统计学特征，不利于短时流量的预测；时间间隔过大则会失去一些随机因素的作用，无法体现随机因素的影响.设在实际交通系统数据采集系统中，检测器以t min作为统计时间间隔，因此，本研究以t min的N倍作为时间间隔，则在观测时间T内交通数据采集个数M=T/t，时间序列数m=T/tN.划分的时间间隔须保证M为整数，从而形成等间隔时间序列.

2.2.2纵向交通流量的水平划分

纵向水平划分对索引变化幅度和预测精度具有较大影响.令最大交通流量F=max（f），其中f为交通流量.将F划分为n段，每段代表1种流量水平，则交通流量水平的段长度为，纵向索引值的变化幅度为 ［1，n］，为满足既反映规律性又反映随机性的要求，n的取值不能太大也不能太小.本研究根据交通流量的历史最大值和最小值，在此基础上加上一个可变量α，减去一个可变量β确定交通流量变化幅度，然后划分为n段，即n个交通流量水平.则有每段长度

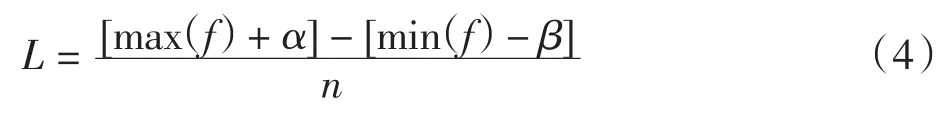
式（4）中：f代表交通流量；α和β为参数；L为整数，可以通过调整α、β和n将L设置为整数.

2.2.3二进制的转化及索引的提取

获取交通状态索引的过程其实是求取流量水平、提取索引序列的过程，即将一维的一串数字变成坐标轴上二维的位置信息.

对某一时间序列有

式（5）中：Li=［min（f）-β］+i×L为第i个时间序列的流量水平，可得序列流量水平0-1矩阵为其中（i∈m，j∈ n），提取流量水平0-1矩阵中bik=1（k∈j）的元素索引，得到序列（1，x1），（2，x2），…，（i，xi），其中行索引i代表时间序列，列索引xi=k通过表示bi的二维位置信息代表预测交通流量数据的间接流量数据.

2.3索引的波动性数据处理

由于GM（1，1）模型自身的缺陷，当数据呈现不规则波动变化时，数据拟合的效果不够理想.本研究采用可以弱化原始数据随机性、提高时间序列规律性的数据处理方法解决此问题.波动性数据处理简单说就是用y（0）（k）+Dk替代y（0）（k），则Dk的求法为：

设原始时间序列为y（0）（k），则

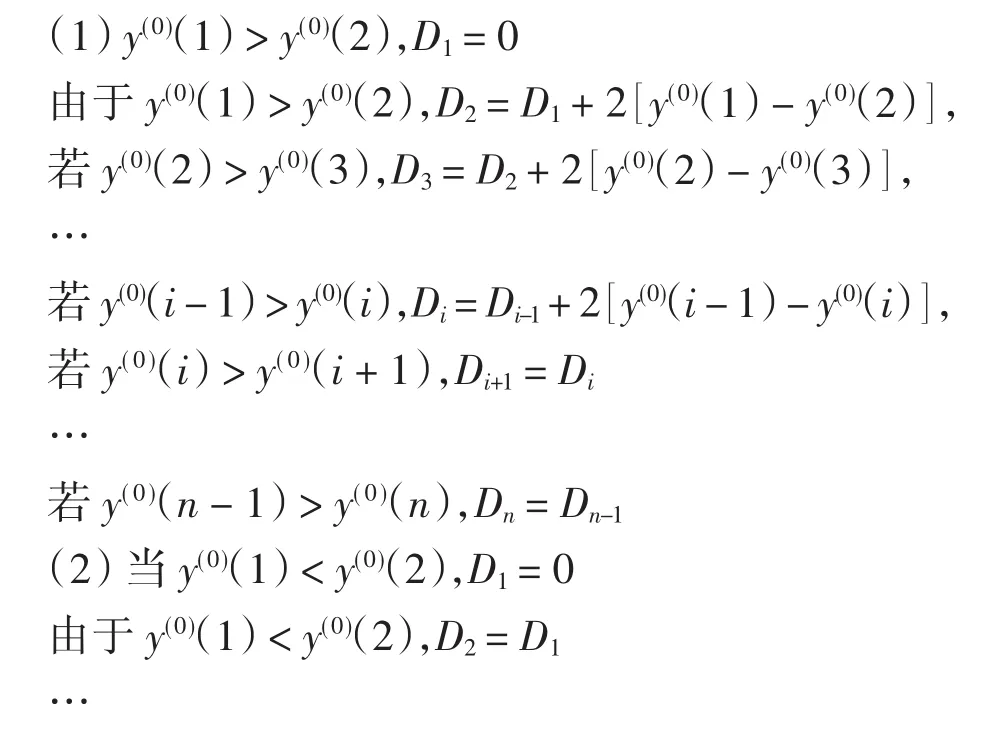
由波动性数据处理方法得到原始数据的处理值为｛x（0）（k）｝，k=1，2，3，…，n，其中x（0）（k）=y（0）（k）+Dk，当y（0）（1）＜y（0）（2）＜…＜y（0）（n）时，可知D1=D2=…= Dn，符合灰色系统理论的原始数据直接生成法.

对｛x（0）（k）｝进行一次累加，得到｛x（1）（k）｝，其中x（1）（k）=

2.4优化模型的应用步骤

在实际应用中，须不断考虑随时间推移进入系统的扰动因素，淡化历史数据，将系统新信息置入序列，建立等维递推信息灰色马尔科夫模型.预测过程中，不断去除旧数据和加入新数据，保持数列等维，直到完成预测目标或达到预测精度为止.

基于二进制序列索引的灰色马尔科夫交通流量预测模型步骤：

（1）原始流量数据处理，包括奇异数据和无效数据处理，构建等间隔时间序列交通流量数据.

（2）时间序列数据的横向和纵向的划分，构建时间序列的二进制矩阵.

（3）二进制矩阵索引的提取.

（4）二进制矩阵索引的预处理.

（5）构建列索引处理后数据的灰色预测模型GM（1，1），得到索引预测值序列

（6）利用波动性数据处理方法的逆方法还原预测值到索引序列.

（7）计算GM（1，1）模型的残差数列e（k）.

（8）利用e（k）、x（0）（k）和划分马尔科夫状态，并近计算一步状态转移矩阵.

（10）预测索引序列x（0）（k）的还原，运用线性插值方法，得到预测的交通流量

（11）更新数据列，新息的加入和旧息的剔除，构建等维递推模型.

（12）返回步骤（2），重复步骤（2）～步骤（11），预测下一时间序列的值.

3　实例验证

3.1数据来源

利用优化后的灰色马尔科夫模型对松原市兴业大街松原大路交叉口某一进口道的交通流量进行验证.预测数据包括所有机动车，原始数据是换算后的当量数据，其中大货车和集装箱的换算系数为3，公交大巴和客车换算系数为2，摩托车换算系数为0.5，其他机动车换算系数为1.数据的采集周期为15 min，流量数据如表1所示.

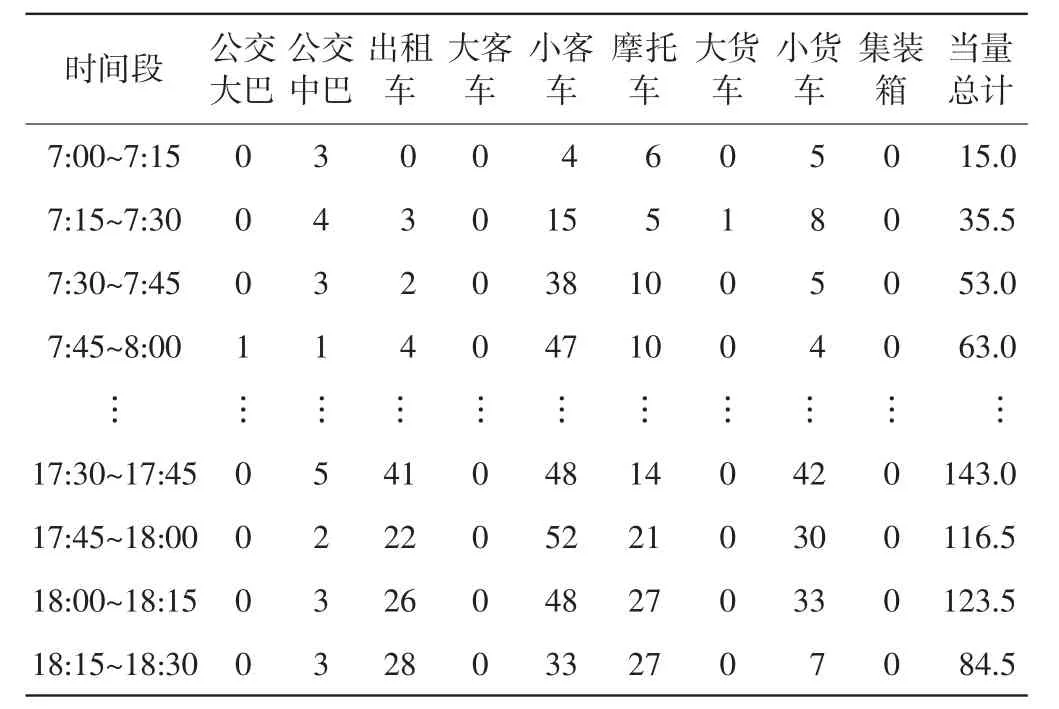
表1　交通流量调查结果Tab.1　Survey results of traffic flow

3.2二进制索引预测

采用基于二进制索引的灰色马尔科夫模型对短时交通流量序列进行模拟预测，预测模型采用的时间间隔为15 min、交通流量纵向划分度为5.信息等维递推可以更好适应于短期预测［16］，为验证新模型方法的实用性，选取前11个交通流量数据进行模拟预测，模型对前10个序列进行预测，第11个为验证数据，第11个以后的交通流量预测方法同前.为验证模型的有效性，分别利用5个不同模型对松原市兴业大街松原大路交叉口某一进口道的交通流量进行预测：

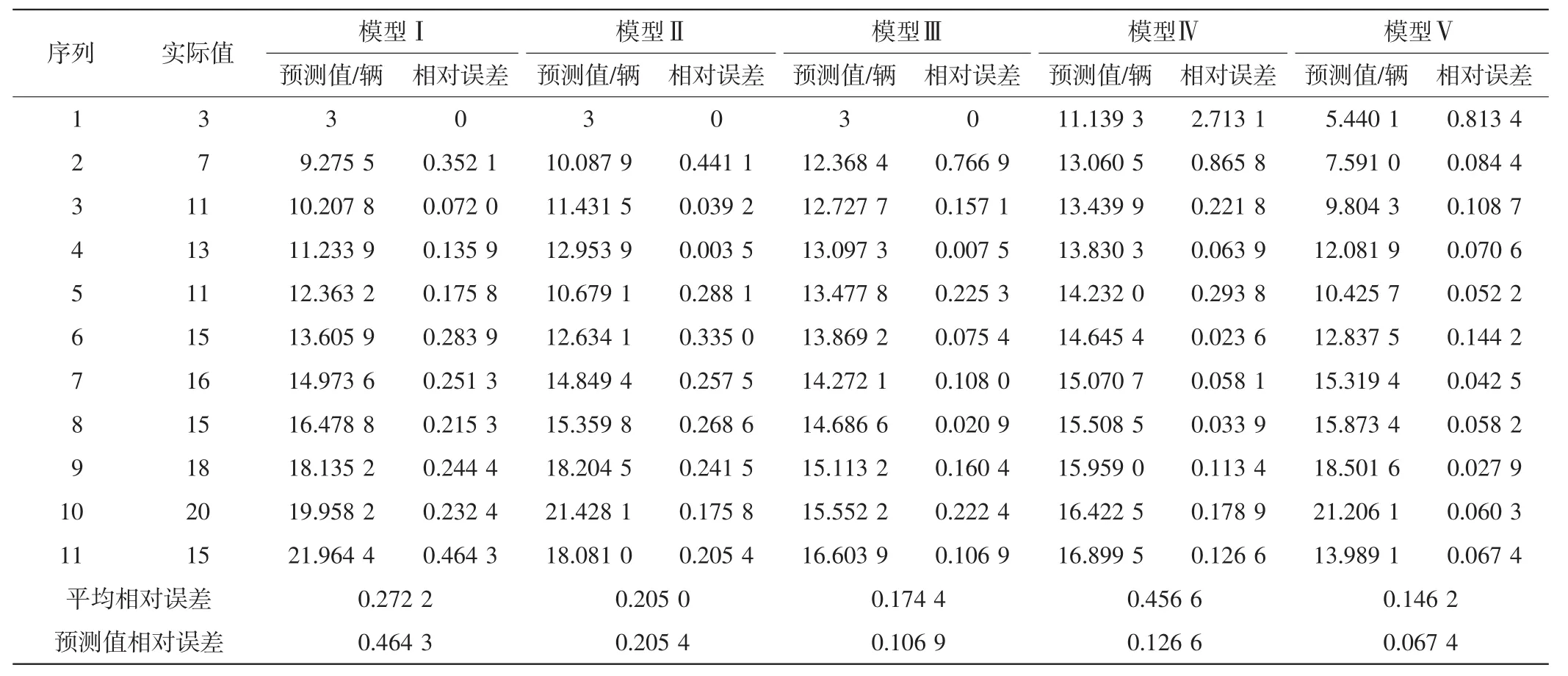
表2　模型预测值与预测相对误差Tab.2　Prediction results and relative error of the models

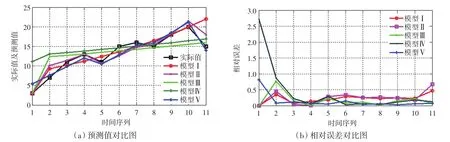
图2　预测结果分析图Fig.2　Analysis diagram of the prediction results

通过对比表2和图2中数据可知，对于波动性数据，传统灰色预测（模型Ⅰ）以第1点为初始条件，曲线既要通过第1点，又要符合最小二乘法，因此在第2点会出现突变，总体得到一条平滑的曲线，所得结果虽然可以大体反映变化趋势，但误差很大，预测值相对误差达到0.464 3；由于波动性数据的处理方法（模型Ⅱ）可以弱化原始数据随机性、提高时间序列规律性，将处理后数据进行灰色预测，因此所得结果优于没进行处理前的预测结果，预测值相对误差降到0.205 4；采用背景值优化方法的灰色模型（模型Ⅲ）克服了传统灰色模型本身算法自带的算法误差，使模型精度进一步的提高，误差降到0.106 9；由于强制初值，造成模型Ⅳ预测模拟的前几个时间序列数值误差较大，拉高了平均误差；而在模型Ⅳ的基础上改进了初选值的灰色模型（模型Ⅴ）则将误差降低至0.067 4.

对比5个模型的预测值可以看出，通过二进制索引、波动性数据处理、背景值优化、初值选为x（1）（n）的灰色模型可以将预测值的精度最大化，是预测短期波动性交通流量的最优方法.

3.3索引还原

4　结论

（1）灰色马尔科夫模型是一种结合灰色系统理论和马尔科夫链的理论的预测模型，在此基础上，通过对原始数据的序列和残差绝对值序列二次建立GM（1，1）预测模型，引进马尔科夫链的状态转移概率矩阵建立了交通量预测模型.

（2）提出二进制索引预测，将直接流量数据变为间接流量数据，减少后期数据处理中误差导致的蝴蝶效应.对灰色模型提出了部分改进措施，通过波动性数据处理方法的逆方法将预测值还原到索引序列，使灰色马尔科夫预测模型可以对波动性数据进行预测，并自主调整预测精度和收敛速度.

（3）结合松原市兴业大街松原大路交叉口某一进口道的短时交通过程的实际交通量数据，建立了其交通量预测模型，研究结果表明：与传统灰色GM（1，1）模型相比，相对误差明显减小，该模型在交通量预测精度上有了很大的改进.

（4）马尔科夫状态的划分没有统一的模式，流量的还原只用了简单的线性插值等，以后会进一步研究优化模型以更好地适用于现实交通流量的实时预测.

［1］靳引利．基于交通量演变模式检索的高速公路交通量预测方法［J］.公路交通科技，2010，27（1）：116-121.JIN Y L.Method of expressway traffic volume forecast based on searching traffic volume evolvement mode［J］.Journal of Highway and Transportation Research and Development，2010，27（1）：116-121（in Chinese）.

［2］聂佩林，余志，何兆成．基于约束卡尔曼滤波的短时交通流量组合预测模型［J］.交通运输工程学报，2008，8（5）：86-90.NIE P L，YV Z，HE Z C.Constrained Kalman filter combined predictor for short-term traffic flow［J］.Journal of Traffic and Transportation Engineering，2008，8（5）：86-90（in Chinese）.

［3］朱中，杨兆升．实时交通量人工神经网络预测模型［J］.中国公路学报，1998，11（4）：89-92.ZHU Z，YANG Z S.A Real-time traffic flow prediction model based on artificia neural network［J］.China Journal of Highway and Transport，1998，11（4）：89-92（in Chinese）.

［4］宫晓燕，汤淑明．基于非参数回归的短时交通流量预测与事件检测综合算法［J］.中国公路学报，2003，16（1）：82-86.GONG X Y，TANG S M.Integrated traffic flow forecasting and traffic incident detection algorithm based on non-parametric regression［J］.China Journal of Highway and Transport，2003，16（1）：82-86（in Chinese）.

［5］张晓利．基于小波分析与神经网络的交通流短时预测方法［J］.信息与控制，2007，36（4）：467-475.ZHANG X L．The forecasting approach for short-term traffic flow based on wavelet analysis and neural network［J］.Information and control，2007，36（4）：467-475（in Chinese）.

［6］樊娜，赵祥模，戴明．短时交通流预测模型［J］.交通运输工程学报，2012，12（4）：114-119.FAN N，ZHAO X M，DAI M.Short-term traffic flow prediction model［J］.Journal of Traffic and Transportation Engineering，2012，12（4）：114-119（in Chinese）.

［7］ZHENG Z D，SU D C.Short-term traffic volume forecasting：a knearest neighbor approach enhanced by constrained linearly sewing principlecomponentalgorithm［J］.TransportationResearchPartC，2014，43（1）：143-157.

［8］张兴强，汪滢，胡庆华．交叉口混合交通流元胞自动机模型及仿真研究［J］．物理学报，2014，63（1）：010508（1）-010508（8）.ZHANG X Q，WANG Y，HU Q H．Research and simulation on cellular automation model of mixed traffic flow at intersection［J］.Acta Phys Sin，2014，63（1），010508（1）-010508（8）（in Chinese）.

［9］陈岳明，萧德云．基于动态交通分配的路网应急疏散模型［J］.清华大学学报：自然科学版，2009，49（8）：1102-1105.CHENG Y M，XIAO D Y.Dynamic traffic assignment-based method for real-time traffic management during emergency evacuation［J］.Tsinghua University：Sci&Tech，2009，49（8）：102-1105（in Chinese）.

［8］MAO Z L，SUN J H.Application of Grey-Markov model in forecasting fire accidents［J］.Procedia Engineering，2011，11：314-318.

［9］KUMAR U，JAIN V K.Time series models（Grey-Markov，grey model with rolling mechanism and singular spectrum analysis）to forecast［10］姚奇富，李翠凤，马华林．灰色系统理论和马尔科夫链相结合的网络流量预测方法［J］.浙江大学学报：理学版，2007，34（4）：396-400.YAO Q F，LI C F，MA H L.Novel network traffic forecasting algorithm based on grey model and Markov chain［J］.Journal of Zhejiang University：Science Edition，2007，34（4）：116-121（in Chinese）.

energy consumption in India［J］.Energy，2010，35：1709-1716.

［11］李相勇，张南，蒋葛夫．道路交通事故灰色马尔科夫预测模型［J］.公路交通科技，2003，20（4）：98-101.LI X Y，ZHANG N，JIANG G F.Grey-Markov model for forecasting road accident［J］.Journal of Highway and Transportation Research and Development，2003，20（4）：98-101（in Chinese）.

［12］孔垂猛，韩印．基于灰色马尔科夫模型的波动性交通流量预测［J］.森林工程，2015，31（1）：92-96.KONG C M，HAN Y.Prediction of volatile traffic volume based on the Grey-Markov model［J］.Forest Engineering，2015，31（1）：92-96（in Chinese）.

［13］韩莹，丰继林．基于二进制串的Trie索引树分词词典机制的研究［J］.计算机与现代化，2013，01（05）：5-7.HAN Y，FENG J L.Research on dictionary mechanism based on binary of Trie Index trees［J］.Computer and Modernization，2013，1（5）：5-7（in Chinese）.

［14］党耀国．灰色预测与决策模型研究［M］．北京：科学出版社，2009.DANG Y G.Grey Forecasting and Study of Decision Model［M］.Beijing：Science Press，2009（in Chinese）.

［15］田刚，李南．江苏省物流货运量灰色预测及灰色关联研究［J］.价格月刊，2010（4）：83-85.TIAN G，LI N.Grey prediction and grey relation research on logistics freight volume in Jiangsu province［J］.Prices Monthly，2010（4）：83-85（in Chinese）.

［16］赵玲，许宏科．基于新维无偏灰色马尔科夫的交通事故预测［J］.计算机工程与应用，2013，49（7）：35-38.ZHAO L，XU H K.Traffic accident prediction based on equal dimensionand new information unbiased Grey-Markov model［J］.Computer Engineering and Application，2013，49（7）：35-38（in Chinese）.

（责任编校亢原彬）

Grey-Markov model for traffic flow forecast based on binary sequence index

YIN Susu，YAN Ling
（Business of Management，University of Shanghai for Science and Technology，Shanghai 200093，China）

For the shortcomings of the short-term traffic flow prediction on precision and convergence speed，a method which combines the binary sequence volatility index and Grey-Markov prediction model was proposed to predict of the short-term traffic flow.The direct traffic data of traditional Grey-Markov model was changed into indirect traffic data by binary sequence index in order to reduce the later data processing error caused by the butterfly effect.Meanwhile the projections were restored into the index sequence using the inverse method of processing method the data with volatility，and the prediction accuracy and convergence speed were actively adjusted.The model was tested with the short-term traffic flow of the intersection of Xinye street and Songyuan street in Songyuan city for example.The results show that relative error of the short-term traffic flow prediction is shortened from 0.46 to 0.07 by using the indirect traffic flow data which indexed by binary sequence for the optimized Grey-Markov model，and the prediction accuracy are significantly improved.The results suggest that the model has better prediction precision，and can satisfy the requirement of short-term traffic flow prediction with higher practicability.

traffic engineering；traffic flow forecast；binary sequence；Grey-Markov model

O211.62

A

1671-1114（2016）02-0033-06

2015-01-12

上海市教委科研创新重点项目（12ZZ137）.

尹素素（1990—），女，硕士研究生.

严凌（1963—），男，副教授，主要从事系统工程方面的研究.