捷联惯导/北斗高精度组合导航方法研究

周　懿，汪小飞，田永锋，郑永梅

(中航飞机股份有限公司汉中飞机分公司，陕西 汉中　723213)



捷联惯导/北斗高精度组合导航方法研究

周懿，汪小飞，田永锋，郑永梅

(中航飞机股份有限公司汉中飞机分公司，陕西 汉中723213)

提出采用紧组合方式进行捷联惯导/北斗组合导航设计，首先对捷联惯导与北斗系统进行误差分析与建模，将捷联惯导系统误差、北斗等效时钟误差相应的距离(伪距误差)以及等效时钟频率误差相应的距离率(伪距率误差)作为组合导航系统状态；利用捷联惯导位置输出与北斗接收机星历输出构造获得等效伪距，将其与北斗接收机测量的伪距对应相减作为量测，推导建立对应的量测方程，采用卡尔曼滤波设计捷联惯导/北斗组合导航滤波算法；仿真结果表明，该组合导航方法的速度精度达到±0.05 m/s，位置精度达到±3.2 m，水平姿态精度达到±0.4′，航向精度达到±1.6′。

捷联惯导系统;北斗导航系统;组合导航;紧组合;伪距

0　引言

高精度导航是制导炸弹、制导炮弹、导弹等高尖端武器实现精确打击的根本保证。目前，国外在诸多制导武器中广泛采用了惯性/GPS组合导航方式，如美国最新研制的高超巡航导弹HyTech计划，采用INS/GPS制导方式，命中精度达到9 m[1]；美军在科索沃战争中使用的联合制导炸弹JDAM采用紧组合方式将惯性测量部件(IMU)与GPS进行组合制导，圆概率误差达到10 m。但是，GPS受美国国防部直接控制，使用权受制于人，对于我国在战时使用势必遇到很大困难，因此惯性/GPS组合导航系统难以直接用于我国国防装备。

目前，我国已经初步建立拥有绝对自主权的北斗卫星导航系统，这意味着可以不依赖于GPS而实现高精度导航定位，为此可将惯导系统与北斗系统结合起来进行组合导航。文献[2-4]研究了采用一代北斗与惯导进行组合导航的方法，其中文献[2,3]将惯导与北斗的位置输出对应相减作为量测，文献[4]将两者的位置、速度输出共同作为量测，两种滤波方法均获得有效收敛，但是其组合导航精度有限，定位精度约为30 m[4]。文献[5]基于北斗二代接收机，采用H∞滤波用于惯性/北斗位置、速度组合模式，有效提高了滤波的稳定性，但组合导航精度仍然有限。文献[6]研究了三星+高度表的无源北斗/INS组合导航方法，将一代北斗接收机测得的伪距作为量测，采用UKF解决量测方程的非线性问题，有效提高了组合导航精度，但滤波算法较为复杂，而且要求北斗的3颗星均能有效搜获；文献[7]将北斗二代接收机输出的伪距作为量测，并采用人工鱼群粒子滤波算法来解决量测方程的非线性问题。

由于基于卫星伪距信息的紧组合方式能够有效提高组合导航系统的抗干扰性[8]，同时能够提高组合导航精度，为此本文采取紧组合方式进行捷联惯导/北斗组合导航设计，并为了避免量测方程的非线性问题，利用捷联惯导位置输出与北斗接收机星历输出解算获得等效伪距，将其与北斗接收机测量的伪距对应相减作为观测量，采用卡尔曼滤波研究组合导航滤波算法。

1　捷联惯导/北斗高精度组合导航方案

由于采取紧组合方式进行捷联惯导/北斗组合导航设计，因此直接利用北斗接收机输出的伪距、星历数据以及捷联惯导输出的导航数据来构造组合导航量测信息，并采用间接法滤波设计，即以捷联惯导和北斗的系统误差作为组合导航滤波器的系统状态。

首先，根据捷联惯导输出的载体位置参数与北斗接收机输出的星历数据，利用相关算法实时解算获得等效伪距ρI；然后，利用该等效伪距ρI与北斗接收机实际输出的伪距ρB相减作为组合导航的量测；接着，将量测送入组合导航滤波器中进行滤波计算，获得系统状态的最优估计结果；最后，利用该估计结果实时地对捷联惯导系统进行误差校正(如图1所示)。

图1　捷联惯导/北斗高精度组合导航的原理方案框图

2　捷联惯导/北斗组合导航系统误差模型与状态方程

为了实现捷联惯导/北斗组合导航滤波器的设计，首先需要分析建立捷联惯导与北斗系统的误差模型，并以此选取组合导航滤波器的系统状态、建立状态方程。

2.1捷联惯导系统的误差模型

由于惯性器件误差是捷联惯导系统最主要的误差源，为此需先建立陀螺仪和加速度计的误差模型。在组合导航设计中，为了尽量降低滤波器状态的维数，同时经过有效的标定补偿后，陀螺仪误差主要考虑常值漂移和白噪声。因此，陀螺仪的误差模型可建立如下：

(1)

同样，加速度计误差则主要考虑常值误差和白噪声，因此其误差模型为：

(2)

由于惯性器件本身存在误差，这就导致捷联惯导系统参数也存在一定误差，具体包括数学平台姿态误差、速度误差、位置误差，上述误差的模型方程可参见有关文献，本文在此就不再赘述。

2.2北斗导航系统的误差模型

北斗导航系统的定位误差实质上是由测距误差所引起，因此直接对其测距误差进行分析建模；而且，文中在设计组合导航滤波算法时采用伪距组合方式，建立北斗系统的测距误差模型(即伪距误差模型)有利于滤波算法设计。

北斗导航系统的大部分测距误差都可以从导航电文中提取相关信息进行有效修正，但是经过修正仍然会存在一些随机误差，这些误差中最主要的是由接收机时钟误差所引起的。因此，北斗导航系统的测距误差可以等效成时钟误差对应的距离，而接收机时钟误差与时钟频率误差之间的关系建模则比较清楚，通常用一阶马尔可夫过程来描述。从而，根据上述分析，北斗导航系统的测距误差模型可以描述如下：

(3)

(4)

其中：δρ为等效时钟误差相应的距离(即伪距误差)，δη为等效时钟频率误差相应的距离率(即伪距率误差)，β为反相关时间常数，wρ、wη为白噪声。

2.3捷联惯导/北斗组合导航的系统状态方程

结合前面所建立的捷联惯导系统与北斗导航系统误差模型，选取捷联惯导/北斗组合导航的状态变量为：捷联惯导的数学平台失准角φE、φN、φU，速度误差δvE、δvN、δvU，位置误差δL、δλ、δh，陀螺随机常值漂移εbx、εby、εbz，加速度计随机常值误差▽bx、▽by、▽bz；北斗导航系统伪距误差δρ，伪距率误差δη。即组合导航系统状态向量X为:

(5)

根据捷联惯导与北斗的系统误差模型，可列写出捷联惯导/北斗组合导航的系统状态方程为:

(6)

其中：F为系统状态矩阵(17×17)；G为系统噪声驱动阵(17×8)；系统白噪声W=[wgx,wgy,wgz,wax,way,waz,wρ,wη]T。

3　捷联惯导/北斗组合导航的量测方程

捷联惯导/北斗组合导航采用紧组合方式，将捷联惯导位置输出对应的等效伪距与北斗接收机输出的伪距分别对应相减作为量测，为此需要首先根据捷联惯导输出的位置信息与北斗接收机输出的星历数据，构造获得与捷联惯导位置输出对应的等效伪距ρI。

设捷联惯导输出位置在地球坐标系中的坐标为(xI,yI,zI)，其可以利用捷联惯导输出的经纬度和高度经过计算而获得；已知北斗导航系统第i颗卫星t时刻在地球坐标系中位置坐标为(xsi,ysi,zsi)，则与捷联惯导位置输出对应的等效伪距ρIi(对应于第i颗卫星)为：

(7)

由于式(7)是非线性方程，需要进行线性化处理，将其相对于载体位置真实值(x,y,z)处展开成展开成泰勒级数，忽略高阶项，只取前两项可得：

(8)

(9)

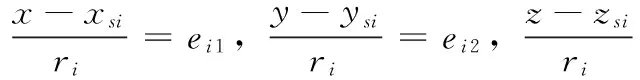
(10)

由于北斗导航系统的伪距误差为δρ，则北斗接收机输出的伪距ρBi(对应于第i颗卫星)可表示为：

(11)

其中：vρi为北斗接收机输出伪距的白噪声。

将计算获得的捷联惯导等效伪距ρIi与北斗接收机输出的伪距ρBi(i=1,2,3,4，分别对应于4颗卫星)相减作为组合导航的量测，记为Z，即:

(12)

将式(10)与(11)代入到式(12)中可得:

(13)

而捷联惯导系统在地球坐标系中的位置误差δx、δy、δz与其在地理坐标系中的位置误差δL、δλ、δh之间满足如下关系：

(14)

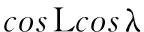
(15)

(16)

于是，将式(14)～(16)代入到式(13)中，经整理可得：

(17)

其中：ai1=-ei1(RN+h)sinLcosλ-ei2(RN+h)sinLsinλ+ei3cosL(RN-RNf2+h)，ai2=-ei1(RN+h)cosLsinλ+ei2(RN+h)cosLcosλ，ai3=ei1cosLcosλ+ei2cosLsinλ+ei3sinL(i=1,2,3,4)。

从而，结合组合导航系统状态向量X，根据式(17)可以列写出捷联惯导/北斗组合导航的量测方程之一为:

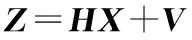
(18)

其中：H为量测矩阵(4×17)，量侧白噪声V=[vρ1,vρ2,vρ3,vρ4]T。

获得组合导航的状态方程和量测方程以后，需要先对它们进行离散化处理，才能使用离散型卡尔曼滤波方程进行组合导航滤波计算。由于量测方程(18)式本身已经是离散的，因此只需将连续的状态方程(6)式离散化为如下形式：

(19)

式中，Φk+1,k为状态一步转移矩阵，Wk为离散化后系统白噪声，其噪声方差阵为Qk。

这里需要说明的是，上述组合导航量测的计算公式(12)和量测方程式(18)是对应于能够搜到4颗卫星的情况下建立的，而如果北斗卫星信号因受丛林、山谷等遮挡导致接收机输出的伪距信息少于4颗卫星，此时只需相应减少量测的维数和量测矩阵的行数，仍可以继续进行组合导航滤波计算。

4　仿真验证与结果分析

图2　载体飞行运动轨迹曲线

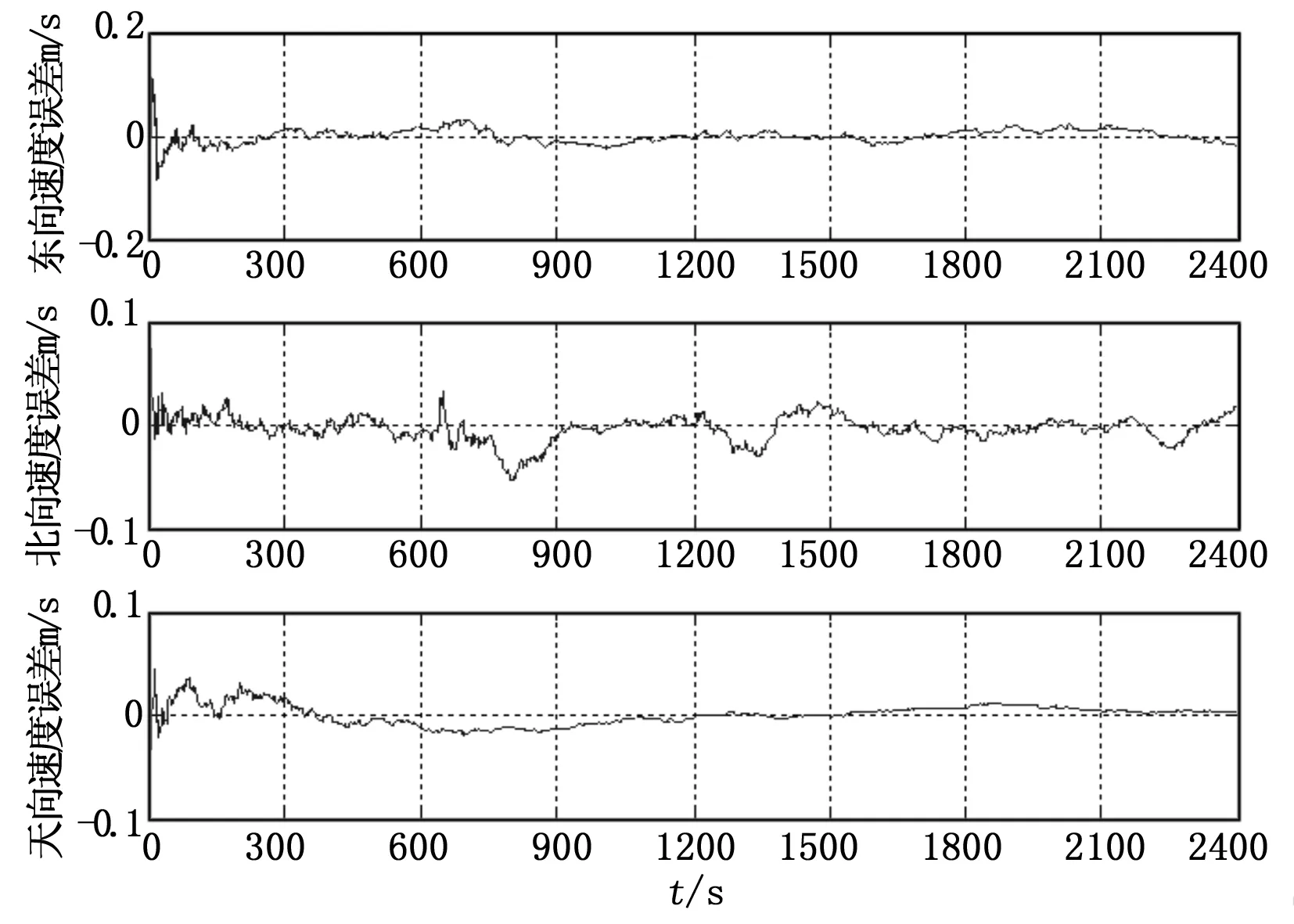
图3　捷联惯导/北斗组合导航的速度误差

图4　捷联惯导/北斗组合导航的位置误差

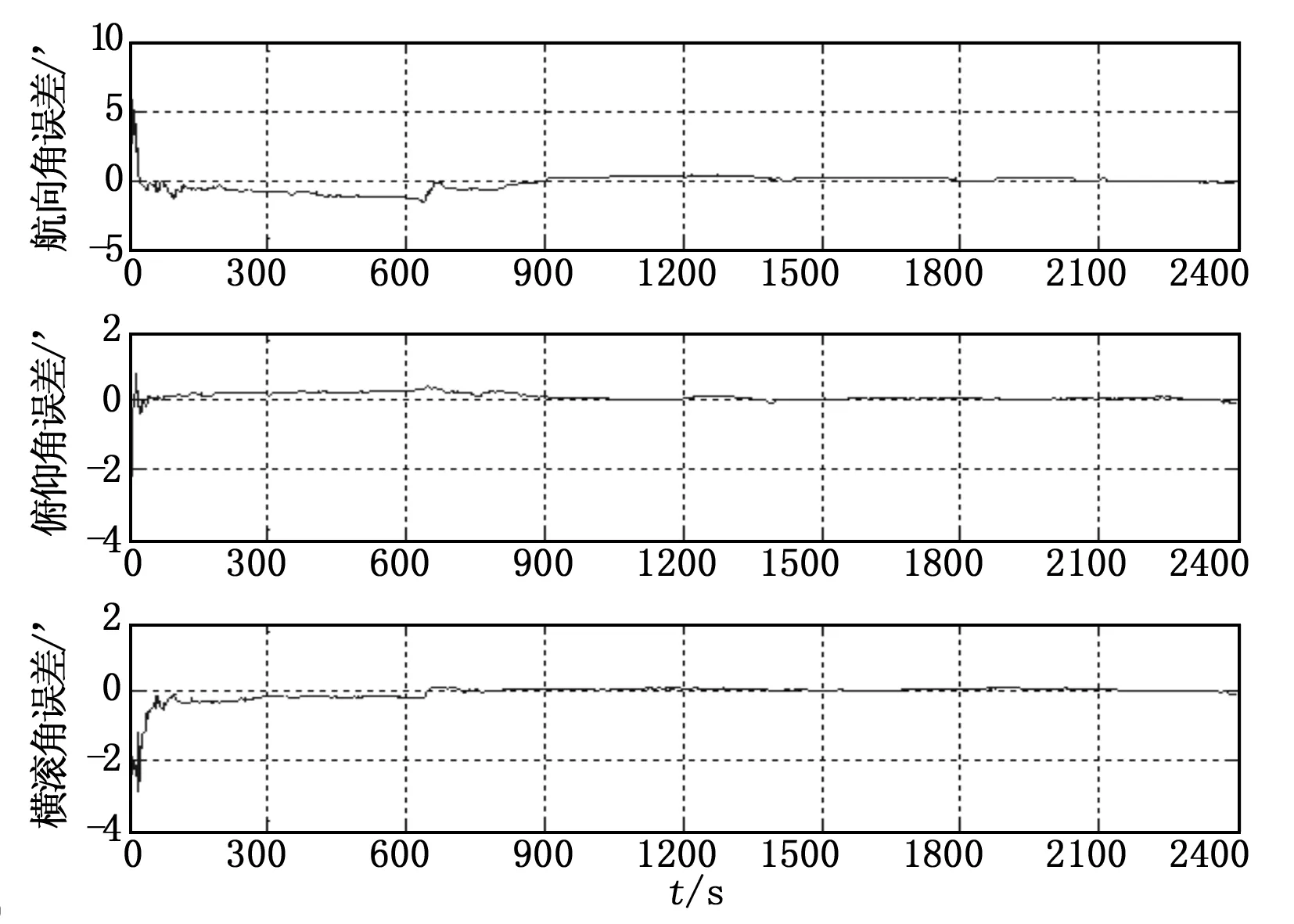
图5　捷联惯导/北斗组合导航的姿态误差

根据上述仿真结果可以看出，捷联惯导系统与北斗导航系统采用紧组合方式后，获得了较高的组合导航精度：速度精度达到±0.05 m/s以内，位置精度达到±3.2 m以内，水平姿态精度达到±0.4′以内，航向精度达到±1.6′以内。这就说明，捷联惯导/北斗组合导航有效克服了纯捷联惯导误差随时间积累的致命缺陷，而且实现了比北斗导航系统更高的导航定位精度。与此同时，仿真结果还表明，尽管飞行过程中载体的运动存在多种机动，但系统导航精度仍然保持稳定，这就意味着载体机动没有对捷联惯导/北斗组合导航精度造成显著影响，从而说明文中所研究的组合导航算法具有较好的鲁棒性。

5　结束语

本文研究了利用捷联惯导系统与北斗导航系统进行高精度组合导航的方法，提出采用紧组合方式进行组合导航设计，将捷联惯导位置输出的等效伪距与北斗接收机测量的伪距对应相减作为量测，并采用卡尔曼滤波研究获得相应的组合导航滤波算法，仿真结果验证了方法的可行性。该方法有效避免了北斗卫星信号因受遮挡而导致定位精度很差的问题，而且实现了较高的组合导航精度，特别是对于我国使用具有绝对自主权。因此，在军事应用领域内将具有重要的意义，非常适用于制导炸弹、制导炮弹、导弹等武器的高精度导航制导。

[1] 李大光. 世界各国高超声速武器发展现状[J].国防技术基础,2007(5): 45-48.

[2] 黄显亮,刘建业,林雪原,等. 北斗双星/SINS组合导航系统滤波模型的一致性研究[J].中国惯性技术学报,2005,13(5): 29-32.

[3] 赖际舟,刘建业,林雪原,等. 基于北斗双星定位系统的组合导航滤波算法实现研究[J].宇航学报,2005,26(1): 107-111.

[4] 扈光锋,马小艳,王艳东,等. 北斗双星/SINS组合导航实时滤波方法[J]. 弹箭与制导学报,2005,25(2): 39-41.

[5] 李艳辉,杨琦. 惯性/北斗组合导航系统的鲁棒H∞滤波[J].吉林大学学报,2015,33(3): 261-266.

[6] 胡攀,高社生,倪龙强,等. UKF滤波在INS/无源北斗组合导航系统中的应用[J]. 弹箭与制导学报,2009,29(5): 69-72.

[7] 李家森,席志红,赵彦青. 北斗/INS组合导航中人工鱼群粒子滤波的应用[J].电子科技,2013,26(6): 157-161.

[8] Vlada S,Goran D,Rade D. Integration of INS,GPS,magnetometer and barometer for improving accuracy navigation of the vehicle [J]. Defence Science Journal,2013,63(5): 451-455.

Research on SINS/BDS Precise Integrated Navigation Method

Zhou Yi，Wang Xiaofei，Tian Yongfeng，Zheng Yongmei

(AVIC Aircraft Co. Ltd. Branch in Hanzhong,Hanzhong723213,China)

Tightly coupled model was adopted to design strapdown inertial navigation system (SINS)/ Bei Dou system (BDS) integrated navigation algorithm. Errors of SINS and BDS were analyzed and modeled firstly. Errors of SINS,pseudo range error and pseudo range rate error of BDS were chosen as states of the integrated navigation system. Position outputs of SINS and satellite ephemeris outputs of BDS receiver were taken to construct the equivalent pseudo range. Then the difference between the equivalent pseudo range and the pseudo measured by BDS receiver was chosen as the measurement,thus the measurement equation is built. Kalman filter was adopted design SINS/BDS integrated navigation filtering algorithm. Simulation results showed that,the velocity accuracy of this integrated navigation method reached ±0.05 m/s,the position accuracy reached ±3.2 m,the horizontal attitude accuracy reached ±0.4′,and the heading accuracy reached ±1.6′.

strapdown inertial navigation system; Beidou system; integrated navigation; tightly coupled; pseudo range

1671-4598(2016)04-0261-04DOI：10.16526/j.cnki.11-4762/tp.2016.04.075

V249.3

A

2015-10-19；

2015-11-11。

周懿(1982-)，男，硕士，工程师，主要从事机载航电系统及测试技术方向的研究。