基于GSPN的飞机测试性指标确定方法研究
王小强,韩 斌
(中航工业第一飞机设计研究院,西安 710089)
基于GSPN的飞机测试性指标确定方法研究
王小强,韩斌
(中航工业第一飞机设计研究院,西安710089)
针对目前飞机测试性指标论证时缺乏有效方法支撑问题,提出了一种基于广义随机Petri网(Generalized Stochastic Petri Nets,GSPN)的测试性指标确定方法;通过分析飞机航线级的维修过程,构建过程的GSPN模型,并对模型进行求解和分析,得到测试性指标与使用可用度和平均修复时间之间的关系,以这两个指标共同作为约束目标,通过权衡分析确定飞机合理的测试性指标,并以某飞机测试性指标论证为例,演示验证了方法的可行性。
测试性指标;广义随机Petri网;使用可用度;平均修复时间
0 引言
测试性是指产品能及时、准确地确定其状态(可工作、不可工作或性能下降程度),并隔离其内部故障的一种设计特性[1]。现代飞机的功能越来越先进,技术和结构复杂性越来越强,各系统的设计也越来越高度集成化和综合化,因此对飞机的故障诊断与隔离提出了更高、更新、更严的要求。在飞机测试性设计之初,首先应确定合理的测试性指标作为输入和依据,过高的指标要求将使产品设计难度、开发周期以及开发费用大幅度地增加,过低的指标要求将不能充分利用系统资源,达不到系统的最终要求[2]。目前在工程研制过程中,确定飞机测试性指标时往往参考类似机型或其它机型的数据,结合工程经验及飞机特点进行确定,主观性太强,缺乏科学依据及方法的支撑。
测试性指标与可靠性、维修性、保障性等指标之间是相互影响、相互约束的,本文依据GSPN的相关理论,构建飞机航线级维修过程的GSPN模型,通过求解模型的稳态概率得到可用度与测试性指标之间的关系,并进一步分析得到平均修复时间与测试性指标的关系,以可用度和平均修复时间作为约束目标,通过权衡分析确定飞机合理的测试性指标。
1 构建维修过程GSPN模型
飞机航线级维修一般包括故障发生、故障检测、故障隔离、故障修复、检测校准等活动,其中故障修复又可根据故障检测、故障隔离的结果进行细化,具体过程如图1所示。
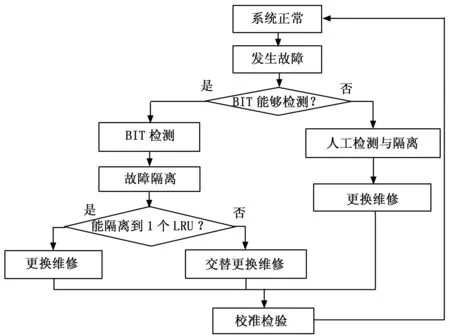
图1 飞机航线级维修过程
广义随机Petri网是SPN的扩展,通过在SPN中引入零延迟时间变迁而得到,通常零延迟时间变迁也称为立即变迁,其变迁优先级高于时间变迁[3]。GSPN模型中变迁有效地描述了时间参数(如任务时间、故障检测时间、故障隔离时间、维修时间等)和概率参数(故障率、故障检测率、故障隔离率等),根据图1的飞机航线级维修过程,构建其GSPN模型,如图2所示。
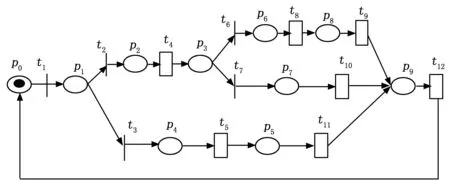
图2 维修过程的GSPN模型
维修过程GSPN模型中的库所和变迁的具体含义如表1所示。
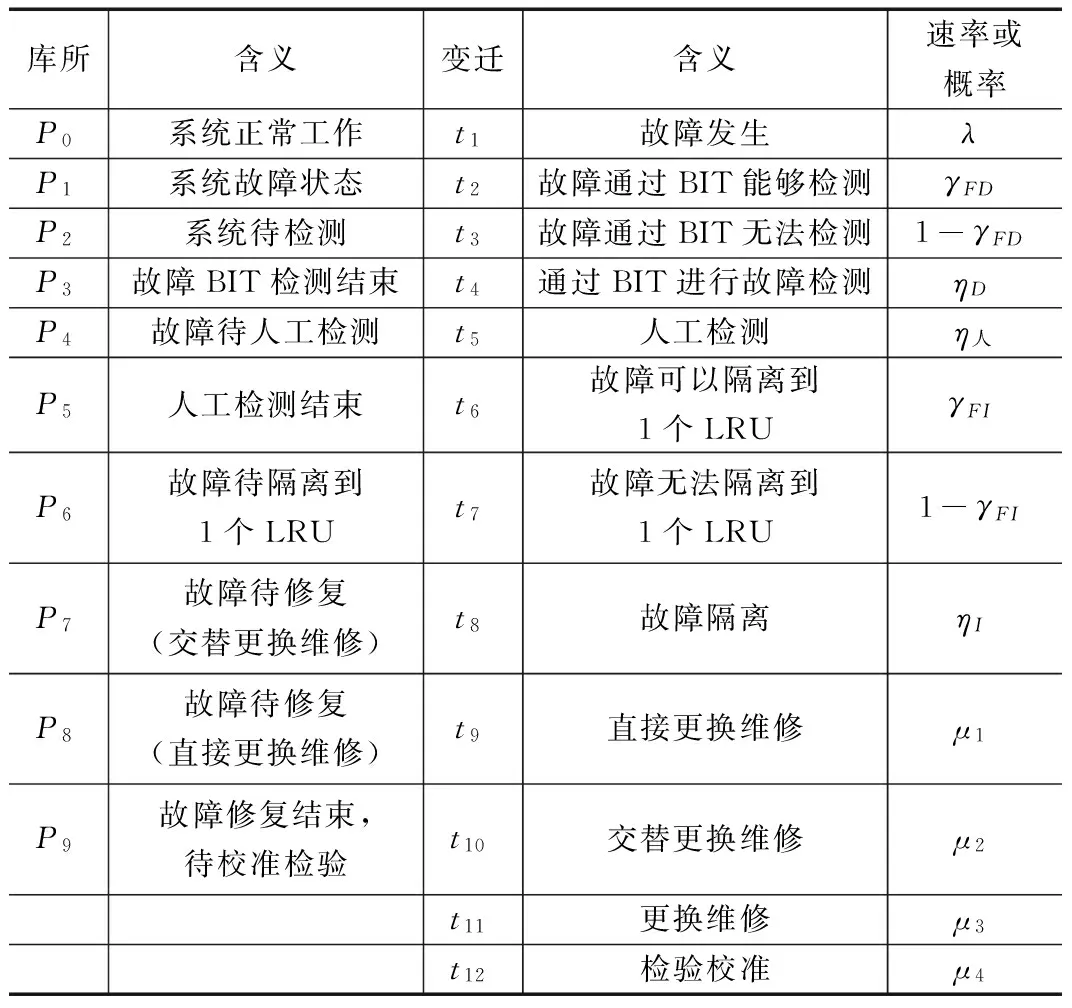
表1 图2中库所和变迁的具体含义
2 模型的求解
从数学上讲,GSPN和连续时间马尔可夫链(continuous time Markov chain,CTMC)是同构的,因此可以采用同构法对系统进行分析[4-5]。设GSPN的可达标识集为S,按照其特性可以分为两个集合T和V,其中T为显状态,是时间变迁集合,V为隐状态,是立即变迁集合。
根据GSPN模型,可以得到状态可达图,基于可达图可以得到系统显状态之间的状态转移矩阵U′,由U′可以得到CTMC的状态转移矩阵Q,矩阵中的元素Qij为:
(1)
设π=[π1,π2,…,πk,…]为系统的显状态概率,则其满足:
(2)
通过求解式(2)可得到系统的稳态概率解。
根据上述理论,对图2构建的维修过程GSPN模型进行求解,过程如下:
1)设可达表示集S={M0,M1,M2,M3,M4,M5,M6,M7,M8,M9} ,其中显状态集T={M0,M2,M3,M5,M6,M7,M8,M9},隐状态集V={M1,M4},从而得到系统的状态可达图,如图3所示。

图3 状态可达图
2)根据图3可以得到显状态的状态转移矩阵为:

(3)
3)根据式(1)构造稳态转移矩阵:
Q=
(4)
4)根据式(2)建立方程组,求系统处于状态M0的稳态概率π0即为系统的稳态使用可用度A0。
(5)
飞机研制过程中维修性常用的指标是平均修复时间(MTTR),它与使用可用度(A0)和平均故障间隔时间(MTBF)之间的关系为:
(6)
通过式(5)和式(6),得出MTTR与测试性指标之间的关系为:
(7)
3 基于GSPN的测试性指标确定方法流程
工程中测试性常用的指标包括采用BIT的故障检测率(γFD)、隔离到1个LRU的故障隔离率(γFI)、平均故障检测时间(1/ηD)、平均故障隔离时间(1/ηI)、人工检测时间(1/η人),式(5)和式(7)分别给出了这些指标与可靠性、维修性和保障性指标之间的约束关系,当可靠性、维修性、保障性指标确定之后,通过权衡分析,可以得到合适的测试性指标值,具体流程如图4。
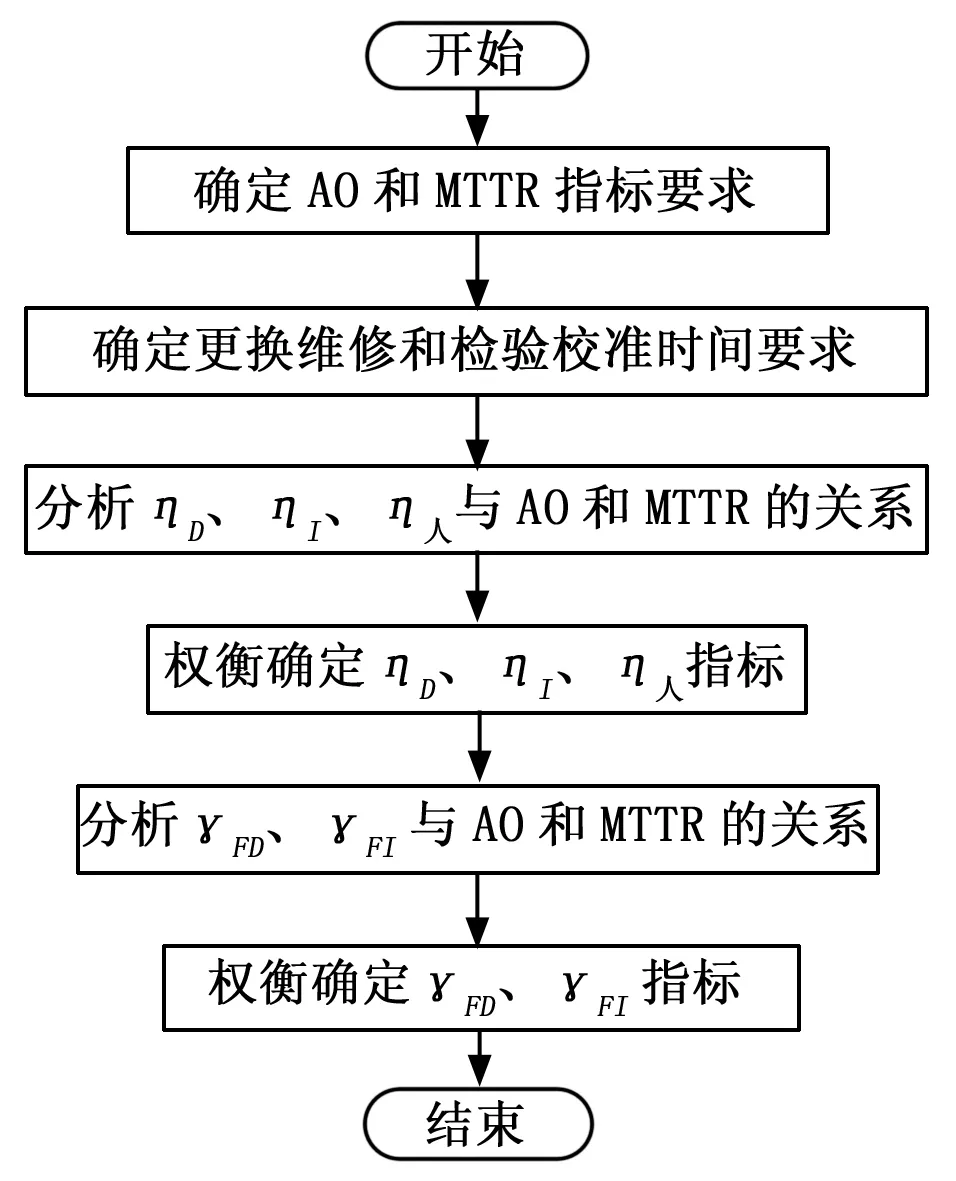
图4基于GSPN的测试性指标确定方法流程
4 工程实例
某飞机指标论证时确定的可靠性指标MFHBF不低于10fh(λ≤1/10),MTTR不大于1.6 h,使用可用度A0不低于0.87,其它与维修相关的指标分别为直接平均更换维修时间1 h(μ1=1 h-1),平均交替更换时间2 h(μ2=1/2 h-1),平均更换维修时间1 h(μ3=1 h-1),平均检测校准时间10 min(μ4=6 h-1),通过上述方法,权衡分析飞机的测试性指标。
将上述已知参数代入式(5)和式(7),设故障检测率和故障隔离率相同,取故障检测率分别为0.7、0.8、0.9、0.95时,分别以故障检测速率、故障隔离速率和人工检测速率为自变量,分析这些参数与使用可用度和MTTR之间的影响关系,结果如图5所示。

图5 影响关系结果图
从图5(a)和图5(b)可以看出,取不同的故障检测率和故障隔离率,随着平均故障检测速率和平均故障隔离速率的增大,MTTR都随之减小,使用可用度A0都随之增大,当速率增大到一定程度时,对MTTR和A0的影响变化已经很小,此时再增大速率对于降低MTTR和提高A0意义不大,相反可能会提高实现成本以及增加系统的复杂性,因此权衡分析取通过BIT进行检测的平均故障检测速率ηD不小于30,平均故障隔离速率ηI不小于30,即平均故障检测时间和平均故障隔离时间均为不大于1/30=2 min。
从图5(c)可以看出,随着平均人工检测速率的增大,MTTR随之减小,A0随之增大,当η人>0.5时,随着平均故障检测速率的增大,故障检测率和故障隔离率对MTTR和A0的影响越来越小,说明此时平均人工检测速率对MTTR和A0的影响已经很小,同时考虑实际中人工检测具有很多不确定性,因此速率也不宜过高,权衡考虑,取η人=1,即平均人工检测隔离时间为1 h。
将确定的ηD、ηI和η人指标值代入式(5)和式(7),取不同的故障隔离率,以故障检测率为自变量,分析其余A0和MTTR的关系,结果如图6所示。

图6 关系图
从图6可以看出,当故障隔离速率为0.8时,要满足A0不小于0.87的要求,故障检测率必须大于0.91,同时要满足MTTR不大于1.6 h的要求,则需故障检测率大于0.76;当故障隔离率为0.85时,要同时满足A0和MTTR要求,则需要故障检测率分别大于0.85和0.72;考虑到实际工程中,故障隔离时应尽可能隔离到单个LRU,避免出现模糊组的情况,因为模糊组的修复时间往往大于直接更换维修时间,同时结合工程实际,考虑设计的可实现性、成本、机载设备的测试性设计水平以及测试性试验结果等因素,故障检测率和故障隔离率也不宜过高,结合因此综合权衡考虑,采用BIT的故障检测率γFD为0.9,隔离到单个LRU的故障检隔离率γFI为0.85。
5 结论
本文以飞机航线级维修过程为基础,构建了过程的GSPN模型,通过模型求解得到测试性指标与使用可用度A0和平均修复时间MTTR之间的关系,依此为基础通过权衡分析确定测试性指标,给出了指标确定方法的具体流程,并以某飞机为例,验证了方法的可行性。该方法有效地构建了测试性与可靠性、维修性和保障性之间的关系,可以用于立项阶段的测试性指标的权衡分析与论证。
[1] GJB2547A-2012.装备测试性工作通用要求[S].北京:国防科工委军标出版社,2012.
[2] 张延生,黄考利,陈建辉,等.复杂装备测试性指标确定方法研究[J].军械工程学院学报,2010,22(6):7-10.
[3] 钱彦岭,邱静,温熙森,等.确定系统级测试性参数的广义随机Petri网模型[J].系统工程与电子技术,2002,24(5):4-7.
[4] 邱静,刘冠军,杨鹏,等.装备测试性建模与设计技术[M].北京:科学出版社,2012.
[5] 苏永定.装备系统测试性需求分析技术研究[D].长沙:国防科学技术大学,2011.
Research on Determination Method for Testability Index of Aircraft Based on GSPN
Wang Xiaoqiang,Han Bin
(AVIC First Aircraft Institute,Xi′an710089,China)
Aiming at the problem of lacking of effective method in the determination of aircraft testability index,a new method is proposed based on Generalized Stochastic Petri Nets. Through analyzing the maintenance process of the aircraft line level,the GSPN model of the process is constructed. Then the model is solved and analyzed. Meantime the relationship between testability index and operational availability and mean time to repair is also obtained. Using the two indexes as a constraint,rational testability index is determined by trade-off analysis. Finally,taking the determination of one aircraft testability index as an example,the feasibility of the method is demonstrated.
testability index;generalized stochastic Petri nets;operational availability;mean time to repair
1671-4598(2016)04-0013-03DOI:10.16526/j.cnki.11-4762/tp.2016.04.004
TP306; V267
A
2015-10-29;
2015-11-27。
航空科学基金2013年度资助项目(2013ZD03016)。
王小强(1985-),男,陕西岐山人,硕士,工程师,主要从事飞机维修性、测试性设计与分析方向的研究。

