基于改进的PSO优化SVM火灾火焰识别算法研究
段锁林,任珏朋,毛 丹,杨 可
(常州大学 机器人研究所,江苏 常州 213164)
基于改进的PSO优化SVM火灾火焰识别算法研究
段锁林,任珏朋,毛丹,杨可
(常州大学 机器人研究所,江苏 常州213164)
针对室内复杂环境下火灾识别准确率会降低的问题,提出了一种改进的粒子群算法优化支持向量机参数进行火灾火焰识别的方法;首先在YCrCb颜色空间进行火焰图像分割,对获得的火焰图像进行预处理并提取相关特征量;其次采用PSO算法搜索SVM的最优核参数和惩罚因子,并在PSO算法中加入变异操作和非线性动态调整惯性权值的方法,加快了搜索SVM最优参数的精度和速度;然后将提取的火焰各个特征量作为训练样本输入SVM模型进行训练,并建立参数优化后的SVM分类器模型;最后将待测试样本输入SVM模型进行分类识别;算法的火灾识别准确率达到94.09%,分类效果明显优于其他分类算法;仿真结果表明,改进的PSO优化SVM算法提高了火焰识别的准确率和实时性,算法的自适应性更强,误判率更低。
火焰检测;支持向量机;粒子群算法;参数优化
0 引言
火灾是一种常见多发,并能造成重大人员和财产损失的灾害,传统火灾检测方法大多基于感温、感烟等传感器[1-2],容易受到外界复杂环境干扰,误报率较高。因此,国内外学者开始涉足图像型火灾探测领域。图像型火灾探测的关键问题是将火灾火焰从有干扰物的环境中分类出来。常见的分类识别方法主要有:贝叶斯分类器[3]、神经网络[4-5]、支持向量机[6-9]等。文献[3]中贝叶斯分类器判别火焰和非火焰取得了比较好的效果,但实际环境中的温度和湿度会发生变化,对发生火灾的先验概率产生影响,进而影响识别精度。文献[5]使用BP神经网络算法对火焰的静态和动态特征进行融合识别,该算法克服了传统方法识别判据单一的缺点,有效地提高了判别准确率。但是神经网络训练过程需要大量样本,导致学习时间过长,且有陷入局部极值导致训练失败的缺点,降低了火灾探测的灵敏度与稳定性。文献[9]通过提取火灾火焰特征量输入SVM模型进行分类识别,文中SVM算法比文献[5] BP神经网络算法所需训练样本更少,因而计算时间也更短,同时在火焰识别准确率方面也更高。但是文中对支持向量机的参数选取不够灵活且参数并非最优,进而影响支持向量机分类性能。
前人的火灾探测算法取得了较好的探测效果,但仍存在局限性,算法在速度、精度和鲁棒性上都存在不足。因此,本文提出一种改进的PSO优化SVM参数[10-12]进行火灾火焰识别的方法。并在PSO中加入变异操作和非线性动态调整惯性权值,提高了对SVM参数寻优的精度和速度,利用获得的最佳参数构建SVM模型进行火灾火焰图像识别。结果表明,本文改进的PSO优化SVM参数的方法能很好地识别复杂环境下的火灾火焰,且识别的精度更高。
1 支持向量机算法
支持向量机是近年来热点研究的基于统计学习理论的机器学习方法,SVM克服了神经网络学习过程中易过学习、易陷入局部极值的缺点,对于较少的训练样本的分类问题效果显著,同时能很好的解决高维数和非线性等问题。通过定义一个非线性映射将对线性不可分的样本数据变换到高维特征向量空间,在这个特征空间构造最佳判定函数,最终求得最佳分类面,使得目标样本中正负两类样本能正确识别并让它们之间的隔离边缘最大化。

(1)
式中,ω′为惯性权重;b为常数;ξ为松弛变量;c为SVM的惩罚参数,求解公式(1),得到ω′和b,进而解得最佳分类面。
SVM将线性不可分的样本数据经过非线性变换Φ:Rd→H,从而让初始空间样本数据变换到高维空间H中,在高维空间H中运用线性方法构造最佳分类面。再运用泛函相关理论,构造合适的内积函数K(xi,xj)满足Mercer条件,即能完成相应非线性转换之后的线性分类。此时,公式(1)目标函数变为:
(2)
式(2)中,αi为拉格朗日乘子。上述问题相当于找到公式(2)仅有的一个最佳解。获得的最佳分类判别函数为:
(3)
式(3)中,函数K(xi,xj)称为核函数,本文选用常用的径向基核函数(RadialBasisFunction简称RBF)作为SVM的核函数。径向基核函数公式为:
(4)
式(4)中,σ为径向基核函数的核参数,将公式(4)代入公式(3),最终的最佳分类判别函数为:
(5)
SVM的惩罚参数c和核参数σ取值大小很大程度上会影响构建的SVM模型的分类效果,惩罚参数c主要调控算法复杂度和分类错误率,其值过大会导致对训练样本分类精度过高,但是对测试样本分类精度低,算法的泛化能力变低;其值过小则对测试样本的分类效果达不到预期目标。而核参数σ值过大会产生过学习现象,算法的泛化能力变低;值过小则欠学习问题突出,SVM模型分类性能过低。支持向量机参数选取没有通用有效解决方法,本文采用改进的PSO算法对SVM的惩罚参数c和核参数σ寻优。
2 粒子群算法及其改进
粒子群算法是根据鸟群捕食方式而提出的一种新的群体智能优化算法。与网格搜索法(gridsearch)和遗传算法 (geneticalgorithm,GA)等传统优化算法有所不同,PSO算法具有实现过程需要调节的参数少、收敛速度快、计算耗时短及搜索精度高等优点,广泛应用于参数优化,能够有效提高搜索效率。
2.1粒子群算法原理
PSO算法中种群的每个粒子的位置被视为优化问题的一个可行解,粒子同时被赋予速度和位置两个特征,粒子的优劣程度通过计算目标函数获得的适应度值来衡量。粒子群迭代过程是根据个体自身和群体最优位置来调节自身行为,从而到达适应度值最好的位置,进而搜索到问题的最佳解。标准粒子群算法公式如下:
Vk+1=ωVk+c1r1(Pk-Xk)+c2r2(Gk-Xk)
(6)
Xk+1=Xk+Vk+1
(7)
上述两个公式中:k为迭代步数;V为粒子的速度;X为粒子的位置;P为个体极值;G为全局极值;ω为惯性权值参数,通常取值范围为[0.2,0.9];r1和r2为随机数,取值范围为[0,1],c1和c2为加速因子,是常量,且为正数,一般设置为c1=c2=2。公式(6)表示粒子下一次迭代速度由上一次迭代的速度、个体极值和全局极值一起确定。公式(7)表示粒子下一次迭代的位置由上一次的位置和迭代后新的速度之和。
2.2改进的粒子群算法
粒子种群在迭代进化过程中如果出现某一粒子找到局部极值,那么其他粒子就会向这个粒子快速聚拢,进而算法陷入局部最优解,也就是常见的早熟收敛现象。因此针对上述问题,本文对粒子之间的聚集程度变化情况进行分析,从而确定全局极值G是否要进行变异操作,迫使陷入早熟收敛的粒子能跳出局部极值进入更大的空间进行搜索,最终搜索到新的个体极值P和全局极值G,照这样的方式进行迭代,直到算法结束即可搜索到问题最佳解。
2.2.1群体适应度方差
粒子的位置可以用适应度函数值来表示,因而,粒子的聚集程度变化对应着粒子适应度函数值的变化。群体适应度方差定义为:设粒子种群数量为n,Fi为第i个粒子的适应度值,Favg为粒子种群当前平均适应度,则群体适应度方差λ2定义为:
(8)
其中:F是标准化定标因子,用于约束λ2的在一定范围,本文F按公式(4)计算:
F=max{1,max{|Fi-Favg|}}
(9)
群体适应度方差λ2体现了粒子种群的聚集状况,若粒子群往一个或某几个位置聚拢,相应的λ2值会变小;反之,表明种群居于任意搜索时期。粒子群算法搜索过程中,粒子逐渐聚集,每个粒子的适应度也趋于一致,所以λ2也也会变小,当粒子聚集到某些位置,算法陷入早熟收敛时,则λ2接近于零。
2.2.2变异操作
在粒子群算法迭代搜索最优解期间,若同时满足公式(10)中λ2=0和搜索到的最佳解不是预期最佳解fd两个条件,则表明PSO算法发生了早熟收敛现象。通过设置随机变换的方式将符合变异的全局极值G按相应的概率pm进行变异,能使粒子跳出找到的全局极值点,进入更大空间寻找新的全局极值,同时,变异也能保证群体的多样性。pm用公式(10)计算:
(10)
公式(10)中的θ取值范围是[0.1,0.3]。λd2通常远小于λ2的最大值。fd为理论最优值,在这里跟支持向量机算法最佳分类精度有关。
对全局极值G进行变异操作,可以使用增加随机扰动的方式,设Gk为G的第k次迭代时取值,η遵循Gauss(0,1)分布,则Gk+1变异用公式(11)计算:
Gk+1=Gk*(1+0.5*η)
(11)
2.2.3非线性惯性权值
为了提高PSO算法平衡全局和局部搜索的能力,通常的做法是采用线性递减惯性权值,在算法初期赋予较大的惯性权值,有益于粒子跳出局部极值,扩大搜索空间;随着粒子群迭代进化,惯性权值逐渐减小,有益于提高粒子在局部空间收敛能力。线性递减惯性权值增强了粒子群算法搜索能力,但粒子实际迭代搜索过程是复杂的非线性变化,线性惯性权值不能有效反映这种特性,对算法的收敛精度和速度上效果不够显著。因此,本文考虑使用非线性递减惯性权值体现粒子群的非线性迭代搜索过程。ω取值用如下公式(12)计算:
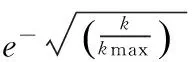
(12)
ωinitial是惯性权值初始值,本文设置为ωinitial=0.2;kmax为最大迭代次数;k为当前迭代次数。
3 基于改进PSO的SVM参数优化
基于改进PSO寻找SVM最优惩罚参数c和核参数σ实现过程如下:
1)设置最大迭代步数kmax,初始化相关参数,同时随机生成粒子的速度和位置。设位置为X=(X1,X2,...,XN),N为粒子种群数量,其中Xi=(Xic,Xiσ)表示第i个粒子由两个分量组成,分别代表支持向量机惩罚参数c和核参数σ的位置,随机生成相应位置的速度为Vi=(Vic,Viσ),同时设定位置两个分量的范围为[Xcmin,Xcmax]和[Xσmin,Xσmax]。
2)计算粒子适应度F(Xi)。以粒子位置分量Xic和Xiσ作为SVM参数并构建火灾火焰分类识别模型,并按公式(14)将5折交叉验证下SVM的分类准确率Y作为粒子适应度F(Xi)。Y用公式(13)计算:
(13)
公式内cc和uc分别为样本数据分类正确和错误的数目。
3)更新粒子群个体极值P和全局极值G。假如粒子适应度值满足条件F(Xik) > F(Xik-1),则Pk=Xk,否则Pk=Xk-1。假如存在某一粒子j满足条件F(Xjk) > F(Xik)均成立,同时满足另一条件F(Xjk) > F(Gk-1),则Gk= Xjk,即粒子j位
置作为全局极值位置,否则Gk=Gk-1
4)根据公式(8)计算群体适应度方差λ2。
5)根据公式(12)设置惯性权值ω。
6)根据公式(10)计算变异概率pm。
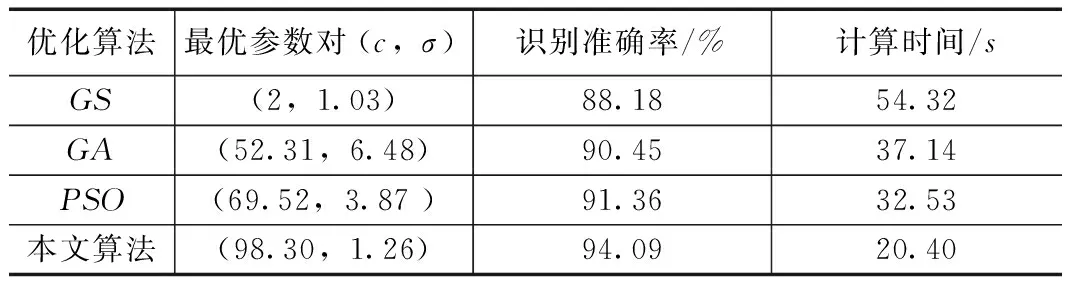
7)产生随机数r∈[0,1],若r 8)根据公式(6)和公式(7)迭代更新粒子群的速度和位置。迭代后要判断粒子位置的两个分量是否在设定的最大搜索范围[Xcmin,Xcmax]和[Xσmin,Xσmax]之内,假如出现超出范围的粒子,必须重新限制粒子到设定范围内。即若Xic 9)判断是否满足退出条件。如果满足最大迭代次数kmax,则退出迭代,同时获得的全局极值G即为最佳参数。 步骤(2)中选取SVM交叉验证的分类准确率来计算粒子适应度F(Xi),基于SVM的火灾分类识别模型的步骤如下: ①获得训练样本集并进行归一化操作。 ②将PSO算法中寻优的核参数σ和惩罚参数c传递到SVM分类模型中。 ③将输入训练样本划分为两类,正确分类样本标签设为1,错误分类样本标签设为-1。 ④通过公式(1)和公式(2)构造对偶模型并求解支持向量机模型,得到二次函数寻优问题的最优解α*=(α1*,α2*,...,αn*)。 ⑤构造公式(5)中的最优分类判别函数。 ⑥通过分类判别函数计算SVM的分类准确率,并将该值返回PSO寻优模型,从而计算粒子适应度F(Xi)的值。 上述算法步骤如图1所示。 图1 改进的PSO对SVM参数寻优流程图 火灾火焰图像识别需要获得图像相关特征量,因此还需经过火焰图像分割、图像特征提取及特征归一化等步骤。 4.1火焰图像分割 本文依据YCrCb颜色空间相关特性进行火焰图像分割,YCrCb颜色空间相比RGB颜色空间能分类彩色图像的亮度信息,并且亮度与色度也存在一定的关联,能够在火焰特征提取的时候兼顾色度和亮度信息。分割获得的图像还需经过腐蚀、膨胀、二值化、边缘检测及中值滤波等过程,才能用于后面的图像特征提取。 4.2火焰特征提取 早期火灾火焰的面积、形态 和颜色不断变化,对火焰的这些特殊特征进行提取,能够作为很好的火灾火焰识别依据。本文选择颜色特征、面积变化率、圆形度、尖角特征、闪烁频率作为火焰图像识别的判据。 1)颜色特征。火灾发生时的颜色信息比较丰富,本文选取YCrCb颜色空间的Y、Cr、Cb3个特征量作为火焰图像识别的判断依据。 2)面积变化率。面积变化率用Varea表示,计算公式为: (14) Z1,Z2为前后两帧图像中的亮点个数。 3)圆形度。圆形度表征物体的相对规整水平,其计算公式为 (15) C为图像圆形度,P和A分别为图像的周长和面积。 4)尖角特征。火灾火焰燃烧时的形状变化明显,火焰尖角个数相对较多。计算尖角个数的方法:起初进行火焰图像边界检测并生成边界链码,然后归一化处理,上升和下降会得到一个三角形,当该三角形顶角和对应的两个边长达到预先设置值时,即获得一个尖角。 5)闪烁频率特征。大多学者研究发现,火焰的闪烁频率受到外界环境变化的影响比较小,将火焰闪烁频率作为火焰特有的特征可以很好的跟其他干扰物区分开来,火焰闪烁频率计算公式: (16) D为火焰等效直径。 4.3特征归一化 不同特征量取值范围差别过大,会造成取值小的特征作用被取值大的特征掩盖,为避免这种影响,需要对不同特征量归一化处理。本文采用高斯归一化到[-1,1]区间。 通过在MATLAB软件上安装libsvm进行了仿真研究,燃烧材质选择纸张,干扰物为蜡烛火焰、照明灯。分别获得340幅火焰图像和260幅干扰图像,样本总共有600组,并将其中380(包括210幅火焰图像和170幅干扰图像)作为训练样本,其余的220幅图像(包括130幅火焰图像和90幅干扰图像)作为测试样本。 然后对采集的图像分割并进行二值化处理,得到二值化图像。如图2、图3和图4所示。 图2 火焰及其二值化图像 图3 蜡烛及其二值化图像 图4 照明灯及其二值化图像 二值图像处理后,还要经过腐蚀、膨胀和边缘提取等处理,然后进行火焰的特征提取,分别获得Y、Cr、Cb、圆形度、面积变化相对速度、尖角及闪烁频率7个火焰特征量,将特征量数据进行归一化处理,并作为SVM分类器模型的训练和测试样本。为了比较不同方法优化得到的SVM模型识别火焰的准确率,本文将传统的网格搜索法(GS)、遗传算法(GA)、粒子群算法(PSO)与本文中改进的PSO算法对SVM惩罚参数c和核参数σ进行优化,并比较建立不同的最优参数的SVM模型后的火灾识别效果。其中,各优化算法的参数设置如下: GA:最大进化迭代次数kmax=80,粒子群体数量N=20,c∈[0.1,1000],σ∈[0.0001,20]。 PSO: 最大进化迭代次数和PSO体数量与遗传算法设置相同,c∈[0.1,1000],σ∈[0.0001,20],c1=c2=2,惯性权值ω=0.9。 本文算法:最大进化迭代次数和粒子群体数量与遗传算法设置相同,c∈[0.1,1000],σ∈[0.0001,20],c1=c2=2,惯性权值ωmax=0.9,ωmin=0.2。 4种算法优化后的SVM模型对火焰图像分类结果如表1所示。表1中采用4种不同的算法优化参数后的SVM模型识别率差距较大,其中,GS算法的火焰识别率只有88.18%,算法精度较低,并且搜索耗时最长,不利于实际应用实时性的要求。GA和PSO算法比GS算法寻找最佳解的速度更快,并且在算法精度方面也有一定的提升,此外,PSO算法在搜索最佳解的效率及解的作用上都好于GA。而本文算法的火焰识别准确率比前面3个算法都要很高,达到了94.09%,算法平均计算时间也是最短的。这是由于改进的PSO算法能在出现早熟收敛时,通过对全局极值G进行变异操作使粒子能跳出当前局部极值,进入更大空间寻找新的全局极值,提高了算法寻找全局最佳解的能力和速度;同时加入非线性调整惯性权值的方式提高了粒子搜索及收敛速度,有效地减少了算法计算时间。改进的PSO算法很大程度上提高了优化支持向量机参数速度和精度,进而提高了SVM模型火焰识别的准确率,并缩短了算法计算时间。 表1 4种算法优化参数的SVM识别结果 本文算法相比贝叶斯分类器和BP神经网络都能更准确的识别出火焰,表2为3种算法的识别结果。其中,贝叶斯分类器识别准确率最低,原因是图像获取过程环境温湿度的变化会影响先验概率,测试和训练样本中火灾和干扰图像所占比例不同也会影响识别准确率。本文算法比BP神经网络识别准确率更高,因为本文算法利用了SVM处理小样本数据的优势,而BP神经网络在小样本条件下分类效果较差。识别结果表明本文算法在识别准确度和速度方面都超过贝叶斯分类器和BP神经网络算法。 表2 3种算法识别结果比较 本文采用构建SVM分类器模型的方法识别室内火灾。首先采用背景差分法进行火焰图像运动区域的检测,在YCrCb颜色空间分割出可疑火焰区域,然后进行火灾火焰图像特征提取,并将特征向量输入SVM训练,并用训练完成的SVM模型对火焰及疑似火焰干扰物作分类识别。为了提高SVM模型火焰识别的准确率,本文提出一种带变异操作和非线性动态调整惯性权值的PSO算法优化SVM的两个参数。仿真结果表明,本文改进的PSO算法进行SVM参数寻优后的分类器模型,在火焰识别准确率和速度方面都有很大的提升,并能有效排除室内常见干扰的影响,降低了火灾探测的误报率。 [1] 王娜.火灾探测的模糊神经网络数据融合算法研究[J].燕山大学学报,2008,32(2):120-123. [2] 张兢.基于多传感器数据融合的智能火灾预警系统[J].计算机工程与应用,2006,6:206-208. [3] 王菲.基于火焰识别的早期火灾探测技术研究[D].广州:华南理工大学,2013. [4] Cheng C X.One fire detection method using neural networks[J].Tsinghua Science and Technology,2011 ,16(1):31-35. [5] 谢荣全,徐志胜.基于BP神经网络在火灾图像探测技术中的应用[J].铁道科学与工程学报,2014,11(3):140-145. [6] Truong T X.Fire flame detection in video sequences using multi-stage pattern recognition techniques[J].Engineering Applications of Artificial Intelligence,2012,25(7):1365-1372. [7] Ko,Byoung Chul,Fire detection based on vision sensor and support vector machines[J].Fire Safety Journal,2009,44(3):322-329. [8] 王媛彬.基于特征融合的图像型火灾探测方法[J].计算机工程,2011,37(19):166-168. [9] 马宗方,程咏梅.基于快速支持向量机的图像型火灾探测算法[J].计算机应用研究,2010,27(10):3985-3987. [10] 付燕,聂亚娜.PSO-SVM算法在肝脏B超图像识别中的应用[J].计算机测量与控制,2012,20(9):2491-2500. [11] Chen Yongqi.LS_SVM Parameters Selection Based on Hybrid Complex Particle Swarm Optimization[J].Energy Procedia,2012,17(A):706-710. [12] Hui ling Chena.Towards an optimal support vector machine classifier using a parallel particle swarm optimization strategy[J]. Applied Mathematics and Computation,2014,239:180-197. [13] 邬月春.基于自适应变异粒子群算法的物流配送路径优化[J].兰州交通大学学报,2012,31(1):114-117. [14] 高磊.一种动态非线性改变惯性权的自适应粒子群优化算法[J].科学技术与工程,2011,11(17):3984-3988. Fire Flame Recognition Algorithm Based On Particle Swarm Optimization-based SVM Duan Suolin,Ren Juepeng,Mao Dan,Yang Ke (Robotics Institute, Changzhou University,Changzhou213164,China) Due to fire detection is relatively low in the case of complex indoor environment,the proposed support vector machine (SVM) is applied to fire detection in the paper,among which an improved particle swarm optimization (PSO) is used to determine optimal parameters of support vector machine. Firstly,the obtained flame image will be processed ahead of time and extracted related feature quantity after flame image segmentation in YCrCb color space. Secondly,the optimal kernel parameter and penalty factor for support vector machine will be found by PSO algorithms,meanwhile,the ability of searching accuracy and speed of the optimal parameters of SVM are raised by adding mutation and nonlinear dynamic adjustment inertia weight in PSO algorithm;Then,each extracted flame characteristic parameters is reserved as training samples to train the SVM model,meanwhile,the SVM classifier model is established after the optimization of the parameters. Finally,the test samples will be input the SVM model to classification and recognition. The accuracy rate of algorithm is 94.09%,and the classification effect is better than other algorithms. Simulation results show that the improved SVM algorithm optimized by PSO can enhance the accuracy and real-time performance of flame recognition,as the same time,the algorithm has better adaptability and lower false positive rate. flame detection; support vector machine; PSO; parameter optimization 1671-4598(2016)04-0202-04DOI:10.16526/j.cnki.11-4762/tp.2016.04.059 TP391.41 A 2015-10-22; 2015-11-18。 江苏省科技支撑计划项目(社会发展)(BEK2013671)。 段锁林(1956-),男,陕西岐山人,博士,教授,主要从事机器视觉与智能移动机器人控制方向的研究。
4 图像采集及处理
5 试验结果与分析



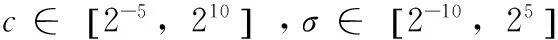

6 结束语

