重心坐标插值的三角形着色算法硬件实现

杜慧敏，季凯柏，蒋忭忭，郭冲宇

(西安邮电大学 电子工程学院，陕西 西安 710121)



重心坐标插值的三角形着色算法硬件实现

杜慧敏，季凯柏，蒋忭忭，郭冲宇

(西安邮电大学 电子工程学院，陕西 西安 710121)

针对三角形的平滑着色技术，设计并实现一种三角形颜色插值的硬件加速器。根据三角形建立单元输入的三角形顶点数据，利用边界方程计算三角形的面积以及面积倒数。通过扫描转化模块筛选出每个三角形覆盖的有效像素块，最后利用三角形建立单元得到的边界方程值与三角形面积倒数值，通过插值模块实现经过扫描转换模块处理后的三角形内所有片元的颜色插值。测试结果表明，该加速器最大工作频率可达约为222.2 MHz，能够实现嵌入式GPU中图形平滑着色的要求。

重心坐标插值；平滑着色；嵌入式GPU

嵌入式图形处理器(Graphic Processing Unit, GPU)可绘制真实感的三维图形, 提高用户的视觉效果，已经成为图形处理技术的研究重点之一[1]。

在嵌入式GPU图形流水线中，三角形着色通常是根据3个顶点的颜色，通过插值的方式计算出光栅化后每个片元的颜色，以便其后对片元进行其他处理，形成屏幕上显示的像素[2-3]。三角形光栅化及片元的属性插值运算量非常大，需要通过高性能硬件加速器实现，才能保证GPU的性能。三角形属性插值有许多种方法，最基本的属性插值算法主要有平面插值算法、透视校正插值算法和重心坐标插值算法[4]。其中,重心坐标插值算法是平面插值算法的一种优化改进，计算复杂度相对低，更适合硬件高效实现[5]。

本文拟通过分析重心坐标插值算法，设计并实现一种三角形颜色插值的硬件加速器。利用光栅化阶段三角形三条边的边界函数值和片元坐标，计算三角形内重心坐标插值所需要的参数，从而对三角形内的片元进行颜色插值，以期满足嵌入式GPU中图形平滑着色的要求。

1　算法概述

1.1三角形重心坐标

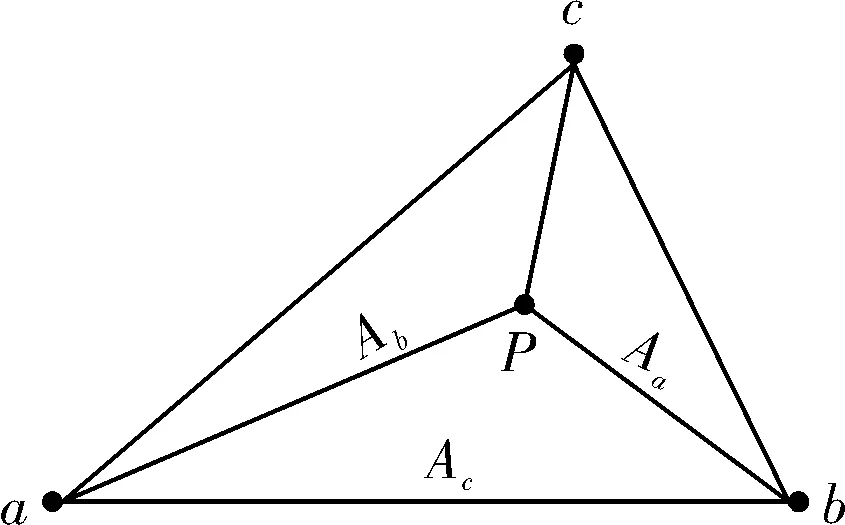
图1　三角形重心坐标插值

三角形abc内任意P点坐标(x,y)可表示为[6]

(1)

(2)

根据P点的边界函数，可将式(2)化简为[7]

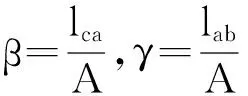
(3)

其中lca为三角形ca边的直线方程，其中lab为三角形ab边的直线方程，且三角形内任意P点重心坐标α，β，γ满足以下关系

α+β+γ=1。

(4)

因此，只需计算其中任意两个，利用式(4)便可快速的计算出第三个插值系数。

1.2基于重心坐标算法的颜色插值

若已知三角形abc的3个顶点的R、G、B颜色值可表示[8]为

(5)

其中Ca为三角形中a点的颜色值，Cb为三角形中b点的颜色值，Cc为三角形中c点的颜色值，CP为三角形中P点的颜色值。

根据三角形内任意P点重心坐标α，β，γ，可将三角形abc内任意P点的颜色值CP[9]表示为

CP=αCa+βCb+γCc。

(6)

根据式(5)和式(6)可知，三角形内任意P点的R,G,B的颜色分量可以表示为

(7)

由式(3)可知，在计算三角形内任意一点的重心坐标时，参数A对于一个特定的三角形图元而言是固定的，因此只需要计算一次，利用光栅化时计算出的边函数可以快速地计算三角形的重心坐标，缩减了整个插值算法的计算量，从而能够加快颜色插值的速度。

2　硬件实现

2.1硬件电路的总体设计

三角形光栅化与重心坐标插值硬件电路顶层主要包括面积计算模块、面积倒数计算模块、重心坐标计算模块和颜色插值模块。硬件电路的总体设计如图2所示。

图2　硬件电路总体设计

对于计算三角形内任意一点的颜色值, 将进行3路并行处理。

熊珍琴[25]等基于Fluent软件，采用RNG-ε非稳态模型模拟了重力影响下的空气源热泵热水器在加热过程中的水箱温度分布情况。仿真结果与实验非常一致，验证了该模型的可靠性，并定性分析了改善水箱盘管布置的方向，为水箱及其同类设备的研发和优化提供了参考。

2.2面积计算模块

采用流水结构实现面积的计算。该流水线结构计算三角形的面积需要有5个浮点a×b功能的加法单元和2个a×b功能的浮点乘法单元。具体的硬件结构如图3所示。其中，MUL代表32位的浮点乘法器，ADD代表32位的浮点加法器。

图3　面积计算的硬件结构

2.3面积倒数计算模块

结合二次多项式逼近算法[10-11]实现三角形建立单元中三角形面积倒数的计算，硬件结构如图4所示。

图4　三角形面积倒数计算的硬件结构

三角形的面积用32bit单精度浮点数格式表示，记为F，则三角形面积的倒数可表示为

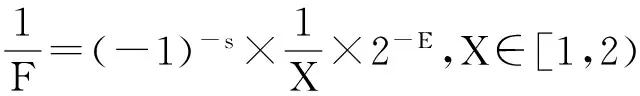
(8)

由式(8)可知，F的倒数计算主要由符号位的计算、尾数位的计算以及指数位的计算3部分组成。符号位和指数位的处理比较简单，且易于硬件实现，在硬件设计中可以和尾数位的计算进行并行处理，不影响电路整体的速度和性能，而尾数位的计算是设计中最为关键和复杂的。 尾数处理的关键在于计算尾数的倒数，通过将尾数区间缩小到[1,2)，利用多项式逼近实现尾数的倒数，减少了计算复杂度。

2.3.1尾数位的倒数计算

尾数位为nbit的二进位小数(包含1位隐藏位)，其范围在[1,2)之间。把X分解为高位X1和低位X2两部分，其中高位X1占mbit，低位X2占n-mbit，具体分解如图5所示。

图5　尾数的分解

由图5可知，X1=[x1x2…xm]，X2=[xm+1xm+2…xn]×2-m，将在归一化的[1,2)区间内分为2m段,每一段的长度为2-m，其中尾数的高m位决定分段的个数。在每一分段区间上进行二次多项式逼近,则任意一个分段X1≤X≤X1+2-m，在一定误差范围内可以用二次多项式近似表示为

f(X)≈AX2+BX+C。

(9)

尾数倒数计算模块主要由查找表、平方运算器和2个乘法融合树组成，硬件结构如图6所示。

图6　尾数倒数计算的硬件结构

2.3.2阶码的调整

已知输入的三角形面积为一个正浮点数(F)，则该浮点的倒数可以表示为

(10)

2.4重心坐标计算模块

重心坐标计算模块主要实现三角形内片元的重心坐标计算。其计算过程如下所示。

第1阶段利用光栅化算出的边函数(lca，lab)是32位浮点数，该模块浮点乘加运算较多，为减少硬件资源开销，保证计算重心坐标时参数lca和lab的精度满足2-16，仿照标准IEEE单精度格式自定义浮点数格式：浮点数用24位表示，其中1位符号位S，7位阶码位E,16位尾数位F，如图7所示。

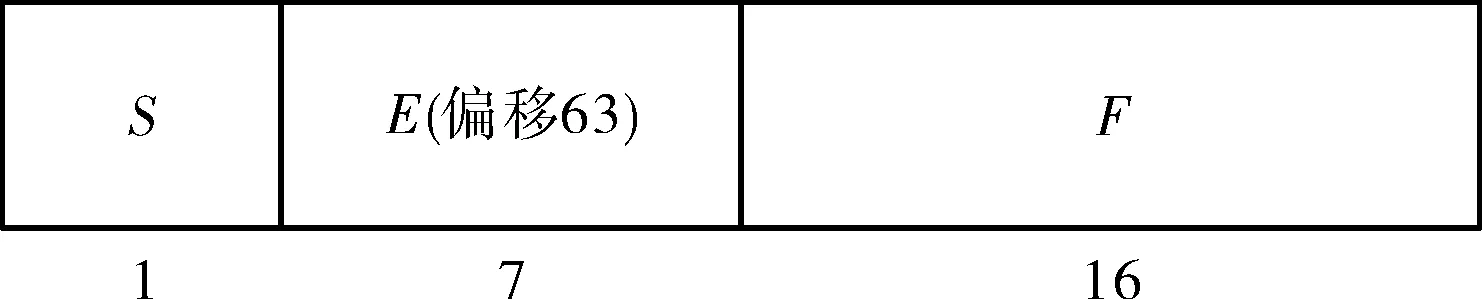
图7　自定义浮点格式

该浮点格式表示的值为

V=(-1)S×2(E-63)×1.F。

(11)

第2阶段完成重心坐标β，γ的计算。需要进行2次浮点乘法运算。

第3阶段完成α的计算，需要进行2次浮点加法运算。硬件结构如图8所示。

图8　重心坐标产生的模块

2.5颜色插值模块

颜色插值模块主要实现了三角形内片元的颜色插值计算。为了缩短三角形内片元颜色值的运算时间，在已知三角形3个顶点的颜色值R,G,B分量及三角形内片元的重心坐标的条件下，采用流水线结构实现三角形内片元的颜色值的计算，如图9所示。其中ADD表示24位的浮点加法器，MUL表示24位的浮点乘法器。

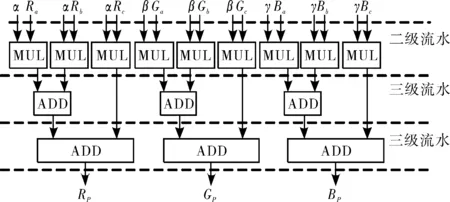
图9　颜色插值流水线结构

3　测试结果与分析

通过分析基于边函数的光栅化和重心插值算法，设计并实现一种三角形颜色插值的硬件加速器，并在Xilinx的ZC706开发平台上移植了Linux操作系统，在Linux操作系统下使用OpenGL ES语言编写简单的图形，进一步对算法进行了验证。

基于重心坐标颜色插值算法的硬件加速器，采用Synopsys DC工具0.13微米工艺综合，频率约为222.2 MHz。在Linux操作系统下使用OpenGL ES语言编写实现的三角形和立方体的平滑着色效果图，如图10所示。

(a) 三角形的平滑着色

4　结语

采用流水线结构以及并行处理的方式，设计并实现一种三角形颜色插值的硬件加速器。测试结果表明，该加速器可实现对任意三角形的平滑着色，能够满足嵌入式GPU中图形平滑着色的要求。

[1]MOSMONDOR M, KOMERICKI H, PANDZIC I. 3D Visualization on mobile devices[J/OL]. Handbook of Research on User Interface Design & Evaluation for Mobile Technology, 2006, 32(2-3):181-191[2016-05-23].http://dx.doi.org/10.1007/s11235-006-9137-3.

[2]TOMAS A M, ERIC H.实时计算机图形学[M]. 2版.普建涛,译.北京:北京大学出版社,2004:213-244.

[3]EDWARD A, DAVE S.交互式计算机图形学[M]. 6版. 张荣华,译.北京:电子工业出版社,2011:107-109.

[4]李玉云. 面向移动设备的光栅化处理器的研究与设计[D]. 合肥:中国科学技术大学, 2010：19-25.

[5]郭安泰,郭立,杨毅,等.一种图形光栅的硬件实现算法[J/OL].中国图象图形学报,2009 14(1):176-182[2016-05-23].http://www.cnki.com.cn/Article/CJFDTotal-ZGTB200901033.htm.

[6]ANAND V B. Computer Graphics and Geometric Modeling for Engineers[M]//New York: John Wiley & Sons,1996:55-68.

[7]SUN C H, TSAO Y M, LOK K H. Universal rasterizer with edge equations and tile-scan triangle traversal algorithm for graphics processing units[C/OL]// ICME’09 Proceedings of the 2009 IEEE international conference on Multimedia and Expo, NJ:IEEE,2009:1358-1361[2016-05-23]. http://dx.doi.org/10.1109/ICME.2009.5202755 .

[8]BROWN R A. Barycentric Coordinates as Interpolants[EB/OL].[2016-05-23].http://arxiv.org/pdf/1308.1279v3.

[9]SKALA V. Duality, barycentric coordinates and intersection computation in projective space with GPU support[J/OL]. Wseas Transactions on Mathematics, 2010, 9(6):407-416[2016-05-23].https://otik.uk.zcu.cz/xmlui/bitstream/handle/11025/11337/Skala_2010_NAUN-journal.pdf?sequence=1.

[10]焦继业, 穆 荣, 郝 跃, 等. 面向移动图形顶点处理器的高性能低功耗定点特殊函数运算单元[J/OL]. 电子与信息学报, 2011, 33(11): 2764-2770[2016-05-23].http://dx.chinadoi.cn/10.3724/SP.J.1146.2011.00480.

[11]牛 涛, 沈海斌. 基于分段二次插值的初等函数逼近低成本设计[J/OL].计算机工程, 2013, 39(8):285-287[2016-05-23].http://dx.chinadoi.cn/10.3969/j.issn.1000-3428.2013.08.063.

[责任编辑：祝剑]

Implementation of triangle tinting algorithm based on the center of gravity coordinate interpolation

DU Huimin,JI Kaibo,JIANG Bianbian,GUO Chongyu

(School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

A hardware accelerator for triangle color interpolation is designed and accomplished. The area of the triangle and area reciprocal are calculated by using the boundary equation with triangle vertex data coming from triangular element. The effective pixel block of each triangle is selected by using the scan conversion module. The boundary value equation and reciprocal of the triangular area obtained from Triangle building unit are then used, and color interpolation of all slice elements in triangle processed by scan conversion module is achieved by using the interpolation module. Testing results show that the accelerator can achieve maximum working frequency of 222.2 MHz, which can achieve embedded GPU graphics smooth rendering.

gravity co-ordinate interpolation, smooth shading, embedded GPU

10.13682/j.issn.2095-6533.2016.05.008

2016-05-23

国家自然科学基金重点资助项目(61136002)；西安市科技发展计划资助项目(CXY1440(10))

杜慧敏 (1966-)，女，博士，教授，从事计算机体系结构和计算机图形学研究。E-mail:228660529@qq.com.

季凯柏(1990-)，男，硕士研究生，研究方向为集成电路系统设计。E-mail:964929756@qq.com.

TP391.4

A

2095-6533(2016)05-0039-04