品味楔形几何体 感悟数学真善美*——2016年全国数学高考理科Ⅰ卷立体几何题解法、评析及思考

●耿合众

(颍上第一中学　安徽阜阳　236200)



品味楔形几何体感悟数学真善美*
——2016年全国数学高考理科Ⅰ卷立体几何题解法、评析及思考

●耿合众

(颍上第一中学安徽阜阳236200)

文章对一道高考数学试题的解法进行探究，试图从外在的形式中多角度寻找数学的本源性东西，在评析过程中思考：什么是学习数学的本质；在进行数学教学时，数学的核心素养的立足点在哪儿.借助对数学问题的品味，感悟数学试题中蕴涵的真善美.

楔形几何体;解法探究;核心素养;真善美

2016年的高考是许多省市从自主命题到统一命题的第1年，笔者所在安徽省使用的是全国Ⅰ卷(即乙卷).纵观理科数学试卷，给人的印象是平稳大气，结构合理,既有内容的真，也有结构的善，更有形式的美，真正体现了能力立意.试题从多方面承载了中学数学的核心价值，多角度对考生的核心素养进行考查，综合检验了考生对数学知识的理解、对数学技能方法的掌握、对数学思想方法的感悟和对数学活动经验的积累.

下面以理科Ⅰ卷立体几何题为例，重温该题的解法探究历程，在简单评析里品味数学的核心内容，从而感悟数学的真善美.

1　试题再现

图1

题目如图1，在以A，B，C，D，E，F为顶点的五面体中，面ABEF为正方形，AF=2FD,∠AFD=90°，且二面角D-AF-E与二面角C-BE-F都是60°.

1)证明：平面ABEF⊥平面EFDC；

2)求二面角E-BC-A的余弦值.

(2016年全国数学高考理科Ⅰ卷第18题)

2　楔形几何体

该题以一个五面体为载体，考查面面垂直的证明和二面角大小的求解.该几何体底面为正方形，顶部为平行于底面的一条线段，4个侧面中有2个是梯形，另2个是三角形，这样的多面体好像木工用的楔，通常称此种几何体为楔形.著名的楔形文字就是因为每一笔画总是由粗到细，像木楔一样而得名.楔形几何体又可看作是三棱柱按对称切割2个小三棱锥后得到的结果.从这个角度来看，该试题是来自生活中的数学，体现了数学中的生活实际，取材于课本中人们熟悉的几何体进行切割.在试题的表现形式上充分体现数学的真善美.

3　问题解决

数学问题的解决，体现了对数学问题本质的理解.用数学的眼光观察问题，用数学的思维分析问题，用数学的语言表达问题.在立体几何中，数学核心素养的五大基本能力(抽象概括、逻辑推理、空间想象、运算求解、数据处理)在该题中的体现尤为突出.

3.1第1)小题，牛刀小试

垂直关系是立体几何的重点内容，绝大多数立体几何问题都与垂直有关，因此垂直关系也成了立体几何的关键.抓住垂直就抓住了立体几何的本质，这话一点不假.第1)小题考查的是面面垂直，自然去想面面垂直的判定定理，从而去找线面垂直，而线面垂直的本质是线线垂直，根据有关垂直关系的定理，把逻辑推理和空间想象用数学符号表达出来，就可以完成证明.

证明由面ABEF为正方形，得

AF⊥FE,

又

∠AFD=90°，

得

AF⊥FD.

在平面EFDC中，FE∩FD=F，AF⊥平面EFDC,AF⊂平面ABEF，从而平面ABEF⊥平面EFDC.

3.2第2)小题，渐入佳境

二面角一直是立体几何考查偏爱的一个知识点，每年都会受到命题者的青睐.在这里表面上是计算二面角的余弦值，实际上把考查空间想象、逻辑推理与数据处理、运算求解等融汇在一起，解决的途径不仅可以采用传统的几何法，还可以用向量法.然而其根本是对楔形几何本质特征的理解和思考.

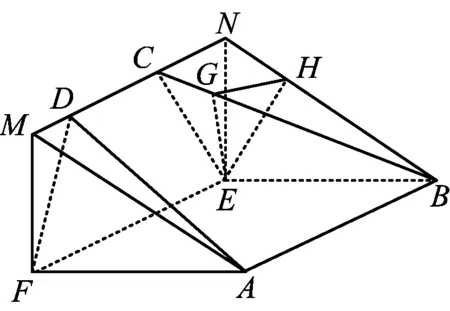
图2

解法1如图2，由面ABEF为正方形，知

AB∥EF,

从而AB∥平面EFDC,

因此

AB∥CD，

即

EF∥CD.

又因为二面角D-AF-E与二面角C-BE-F都是60°，且AF⊥平面EFDC，AF∥BE,所以

∠DFE=∠CEF=60°，

从而四边形是等腰梯形，将其补成矩形EFMN.联结MA，MF，NB，NE，易得MAF-NBE为直三棱柱.

平面NBE⊥平面ABNM，交线为BN，在平面NBE中，作EH⊥BN，垂足为H.在平面ABNM中，过点H作HG⊥BC，垂足为G，联结EG，易得EG⊥BC,于是∠HGE是二面角E-BC-N的平面角，而二面角E-BC-N与二面角E-BC-A互补，因此二面角E-BC-A的余弦值是∠HGE余弦值的相反数.又AF=2FD，设FD=1=CE，AF=2=BE，且BE⊥平面EFMN,得

在Rt△NEB中，

在Rt△CEB中，

在Rt△EHG中，

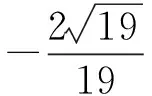
评注该解法立足于楔形几何体的本质特征，还原切割前直三棱柱的本来模样，充分体现转化和化归思想.解题，就是退，退到不能再退的时候，问题的本源也就清楚了.

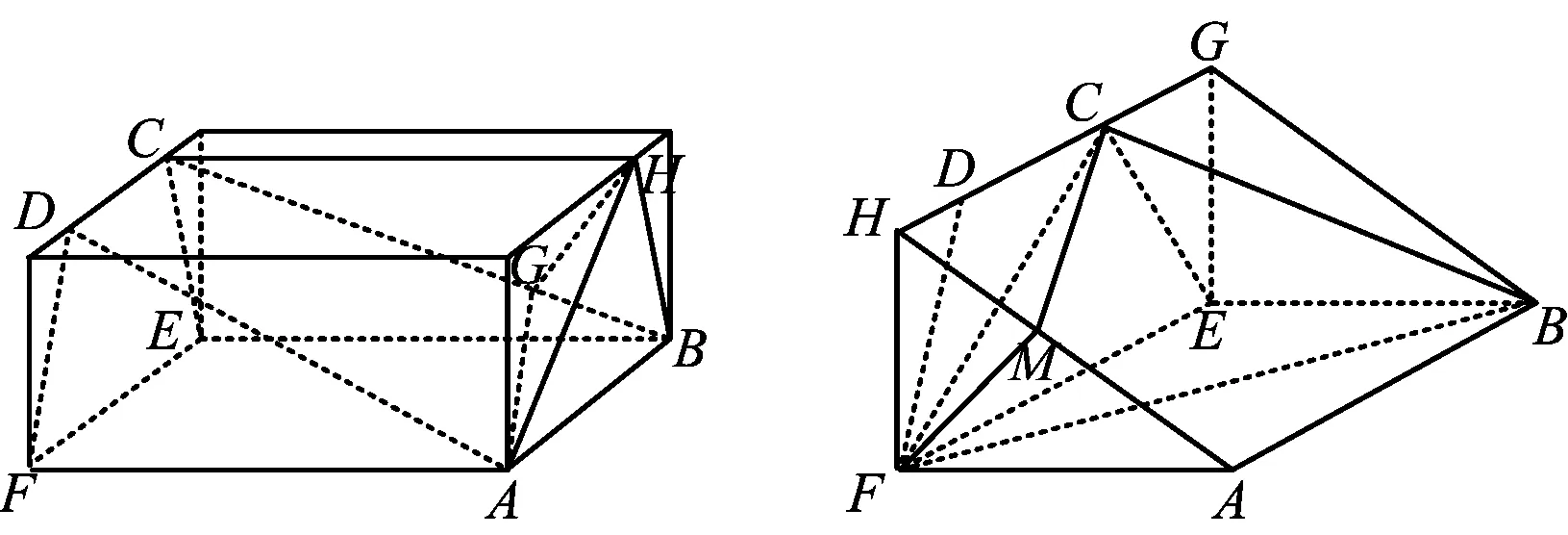
图3

于是

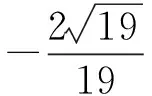
评注该解法把问题回归到长方体之中.长方体是立体几何最重要的载体之一，很多几何体都可以补全为长方体，使得相应的证明和计算都更为清晰和容易，也更能弄清空间点线面的位置关系和数量关系.

解法3由解法1知

∠DFE=∠CEF=60°.

由AB∥EF，AB⊄平面EFDC，EF⊂平面EFDC，知AB∥平面ABCD,AB⊂平面ABCD，且平面ABCD∩平面EFDC=CD，于是

AB∥CD，

从而

CD∥EF，

知四边形EFDC为等腰梯形，可得

∠CDF=∠DCE=120°,DC=DF,

∠DCF=30°,∠FCE=90°,

即FC⊥CE.又EB⊥平面EFHG,CF⊂平面EFHG，则CF⊥EB，故CF⊥平面CEB，得平面CFB⊥平面CEB.

在平面FHA内过点F作FM⊥AH交AH于点M，则FM⊥平面CBA.由CF⊥CB，则∠FCM是二面角F-BC-A的平面角，设其为α.又由题设EF=EB=2，EC=1，知

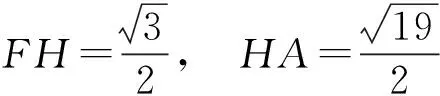
得

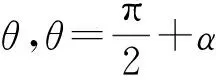
评注该解法把所求二面角分成一个直二面角和一个锐二面角的和，而其中锐二面角大小比较容易求解，这也是求钝二面角常见的方法之一.

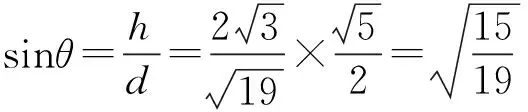
由题意知θ为钝角，故

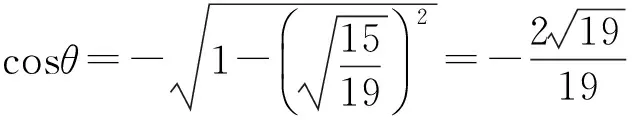
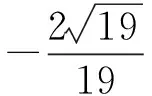
评注该解法回避了找二面角平面角的过程，有时二面角的问题难就难在“找”和“证”上.在一个半平面里选一点，求出该点到另一个半平面的距离和到二面角棱的距离，就可以去求二面角平面角的正弦值了，而这2个距离，利用等体积和等面积就能轻松确定.

解法5由解法1知

∠DFE=∠CEF=60°.

由AB∥平面CEF，得AB∥CD，EF∥CD，易得四边形CDEF与四边形ABEF均为等腰梯形.如图4，过点A作AH⊥BC于点H，过点H作HP⊥BC交BE于点P，则∠AHP为二面角E-BC-A的平面角.令DF=1，则

过点C作CO⊥AB于点O，则

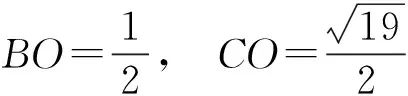
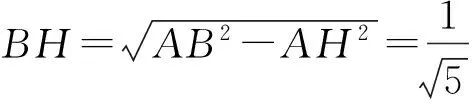
由△BHP∽△BEC得

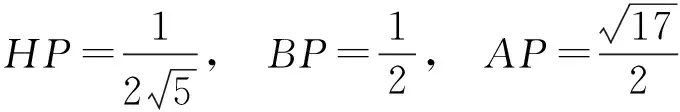
在△AHP中，由余弦定理得

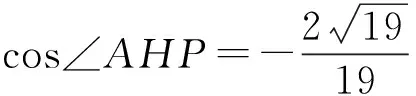
评注解法5先选取与二面角的2个半平面都相交的一个平面α，在二面角的一个半平面与平面α的交线上选一点向二面角的棱作垂线，再由该垂足在二面角的另一个半平面内作二面角棱的垂线，与平面α的交线交于一点，这2条垂线形成的角就是二面角的平面角，求出刚才3个点组成的三角形3条边长，利用余弦定理即可获解.

图4 图5

解法6如图5，由面ABEF为正方形，得

AB∥EF，

从而

AB∥平面EFDC，

因此

AB∥CD，

即

EF∥CD.

又二面角D-AF-E与二面角C-BE-F都是60°，且AF⊥平面EFDC，AF∥BE，得

∠DFE=∠CEF=60°,

则四边形EFDC和四边形ABCD都是等腰梯形.

由AF=2FD，设FD=1=CE，AF=2=BE，且BE⊥平面EFMN，CD=1,于是在Rt△CEB中，作EH⊥BC，垂足为H，则

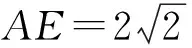
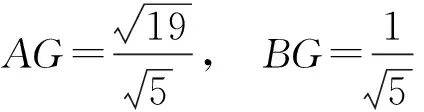
从而

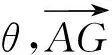
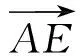
即

解得

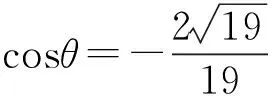
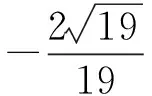
评注该解法从二面角中选择以二面角的棱为公共边的2个三角形，分别从二面角的棱外三角形顶点向棱作垂线，根据所给出的条件，利用解三角形知识求出相关线段的长.再利用向量夹角和二面角大小关系，由向量回路寻找等式，借助向量的模长和数量积得出二面角余弦值的关系式.

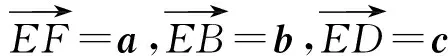
记平面EBC的一个法向量为

n1=xa+yb+zc，

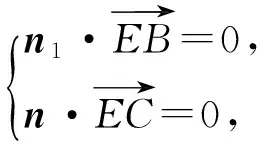
令x=1，z=-1，则n1=a-c.记平面ABC的一个法向量为

n2=xa+yb+zc，

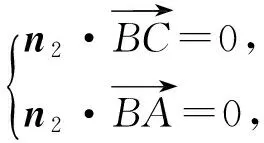
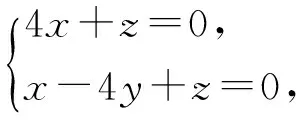
令x=4，y=-3，z=-16，则

n2=4a-3b-16c.

因为

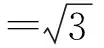
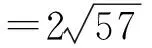
n1·n2=12，

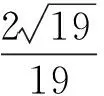
评注该解法是向量法的一种——基向量法，这种解法容易被忽视.只要在几何体中找到从一点出发的3条线段的长度和夹角，就可以选定为空间向量的一个基底，剩下的就是数据计算的事了.

解法8由第1)小题知

∠DFE=∠CEF=60°,

因为AB∥EF，AB⊄平面EFDC，EF⊂平面EFDC，所以AB∥平面EFDC.又AB⊂平面ABCD,平面ABCD∩平面EFDC=CD,则AB∥CD，从而CD∥EF，四边形EFDC为等腰梯形，且平面ABEF⊥平面EFDC.

图6

建立如图6所示的空间直角坐标系E-xyz.

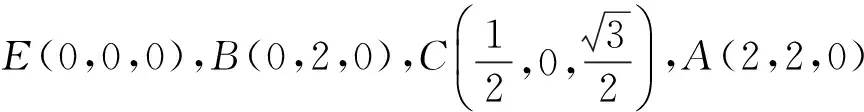
得

y1=0,

z1=-1,

即

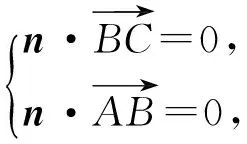
得

x2=0,

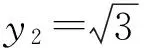
设二面角E-BC-A的大小为θ，则

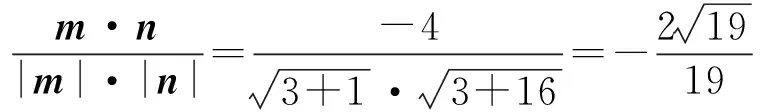
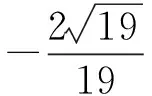
评注坐标法主要是利用向量的相关知识及其运算来解决问题，即用代数的方法解决几何问题.将形转化为数来解决，降低了立体几何的思维难度，解题思路有一定的规律性，便于学生掌握.但寻找并判断从一点出发的3条两两垂直的直线是重点，也是难点.

4　一些思考

今后将有更多的省市加入全国卷统一命题的行列，对全国卷进行评析和思考是一件有价值和有意义的事情.而对全国卷的适应及思路的调整将是一个必然的过程，全国卷的试题更加体现命题的“能力立意”这一原则，更能深入到数学的本质，更能体现数学的意蕴，并且对数学核心素养的形成和培养目的非常明确.

说到数学核心素养，离不开数学的学习、应用和创新.综合体现在发现与提出问题、分析与解决问题的过程之中.数学知识是高度抽象的，它的语言(特别是数学符号、图表语言)是高度概括、凝练的.正是这种高度的抽象性才使数学成为连接现实世界与人类智慧的桥梁，使数学语言成为表达客观世界结构的唯一精准语言.立体几何正紧紧围绕“数量关系”“空间形式”“数形结合”和“公理化思想”这4条主线，让学生有机会体会和认识一些数学本源性问题.对立体几何问题的解决，传统几何法的角度，现代向量或向量坐标法的途径都是对该类问题本质的考量，空间想象能力、逻辑思维能力、推理论证能力、数据处理能力和运算求解能力都也是对数和形这两大关系的深刻理解.

在今后的数学教学中，不仅要紧紧抓住对基础知识、基本技能的掌握，还要重点提高对数学思想方法和数学本质的理解，更重要的是培养学生继续学习的潜能，从而努力实现数学核心素养的形成和促进人的发展.最终在品味数学的过程中，充分感悟数学的真善美.

16-06-27；

2016-07-27

耿合众(1974-)，男，安徽颍上人，中学高级教师.研究方向：数学教育.

O123.2

A

1003-6407(2016)10-42-05