一样的风景 更高的追求*——2016年浙江省数学高考立体几何题评析

●卢　明

(元济高级中学　浙江海盐　314300)



一样的风景更高的追求*
——2016年浙江省数学高考立体几何题评析

●卢明

(元济高级中学浙江海盐314300)

2016年浙江省数学高考立体几何试题的特点是：保持风格，突出重点；稳中有变，突出素养．通过对试题的背景分析和解法探讨，感受到了命题人对数学知识、数学思想以及数学核心素养考查的新理解、新思考，从而悟得对高中立体几何教学的启示：严格按“标准”教学；重视“建系”方式的价值追问；加强推理论证能力的培养；提高画立体图的能力．

数学高考;立体几何题;评析;核心素养

2016年高考已尘埃落定，为“3+综合+IB模块”的老高考模式画上了圆满的句号．透过2016年浙江省数学高考立体几何试题，读到了命题人对数学知识、数学思想以及数学核心素养考查的新理解、新思考，这将对2017年起浙江实施的“必考+选考”新高考模式背景下的高中数学教学有积极的指导意义．

1　试卷命题情况回顾

总体而言，2016年的立体几何试题还是比较平稳的，但是也有明显的变化．具体来说体现在以下几个方面：

1.1保持风格，突出重点

试题继续保持以往的浙江命题风格和考查重点，考查空间点、线、面的位置关系以及三视图、线线角、线面角、二面角、空间向量的应用等基础知识、推理论证能力、空间想象能力和运算求解能力，并且文、理科试题有同也有别．如选择题，考查空间线、面位置关系的判定，文、理科试题相同，且题次都是第2题．填空题，文科第9题、理科第10题，都考查三视图、几何体的表面积和体积；文科第14题和理科第14题，本质都是“动态”情境的立体几何题，但是描述方式有所不同，文科比较直白，直接点明“翻折”，理科则比较隐秘，其实本质也是“翻折”，求解结论文、理科有别，文科求线线角的最值问题，理科求体积的最值问题；填空题的难度理科略高于文科，体现文理有别，但是差距不大．解答题，文、理科试题背景一致，都是三棱台，且第1)小题文、理科一样，考查线面垂直的证明，第2)小题文、理科有别，文科考查线面角，理科考查二面角，理科难度明显高于文科．

1.2稳中有变，突出素养

立体几何试题更加突出了对能力与素养的要求，比如“向量法”的应用，对“建系”的能力要求略高于往年，此外，还体现在以下几个方面：

1)分值的变化．2016年的文、理科立体几何题都是考查1道选择题、2道填空题、1道解答题，总分均为30分，比前3年的分值有所增加．回顾前3年的试题情况，2013年和2014年的文、理科都是考查2道小题、1道大题，总分均为24分；2015年的文科考查2道选择题、1道解答题，总分为25分，理科考查2道选择题、1道填空题、1道解答题，总分为29分，理科分值高于文科．2015年和2016年的立体几何分值高于2013年和2014年，其中一个原因是高考内容减少了概率与统计．

2)题型的变化．2013年和2014年的立体几何试题都是静态情境的；2015年的理科立体几何试题(第8题)是“动态”情境的(翻折)，文科没有“动态”情境的题；2016年的文科填空题第14题也引进了“动态”情境题，显然，对文科生空间想象能力的考查要求有所提高．

3)难度的变化．2015年和2016年增加的“动态”情境立体几何题，难度都比较高，处于“压轴”或“次压轴”的水平，而2016年理科第14题的难度明显高于2015年的第8题，文科立体几何试题的整体难度较往年也有所提升．

4)背景的变化．之前的3年，文、理科立体几何解答题的背景都是学生比较熟悉的锥体或柱体，2016年的试题背景不落俗套，选择了师生平时都不太关注的棱台，体现了一种情境创新．尽管试题设问依然常规，但是，对学生的要求明显提高．事实也是如此，立体几何解答题，理科全省平均分为10.89，难度系数0.72，文科平均分为8.66，难度系数0.58．理科平均分还算理想的原因之一是因为用“向量法”能够避开棱台的定义，降低推理论证的难度．

总之，从2016年的立体几何试题所释放出的信息看，文、理科难度有“接近”的趋势，以笔者之见，也许这是在为今后新高考方案——数学“文理合卷”作铺垫．

2　解法探讨

图1

例1如图1，在△ABC中，AB=BC=2，∠ABC=120°，若平面ABC外的一点P和线段AC上的一点D，满足PD=DA，PB=BA，则四面体PBCD体积的最大值是______．

(2016年浙江省数学高考理科试题第14题)

笔者在与考生的交流中了解到，本题能得到正确答案的考生有不少．但深究他们的解法时，大部分考生的回答是选择特殊位置来解，即让点D位于AC的中点，且PD⊥面ABC.此时

于是

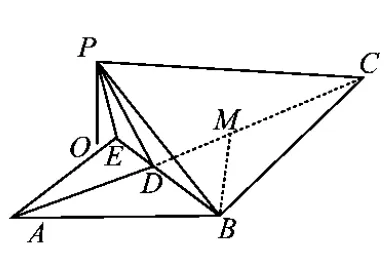
图2

图3

由条件知△PBD是由△ABD沿直线BD翻折而得，联结AE，则AE⊥BD，且AE=d．如图3，设AD=x，则

易知BM=1,由△AED∽△BMD得

点评本题中，由于当且仅当点D为AC的中点，且面PAC⊥面ABC，面PBD⊥面ABC时，VP-DBC取到最大值．正因为四面体体积的最大值是在上述特殊位置时取到的，所以给学生“蒙对”本题答案提供了可能．

此外，本题所含的知识点比较多，它将平面几何、立体几何、函数等知识综合在一起，对其进行正面解答，其运算量不亚于一道立体几何解答题．尤其是在求体积的最大值时，要将四面体PBCD的底面BDC上的高转化为点A到线段BD的距离，才能建立函数关系，这一点考生难以想到，并且所得到的函数关系式的最值也不好求．故本题的综合程度相当高，运算量较大，按照以往浙江命题风格——“小题小做”，作为“小题”的知识点和运算量应该有所控制，因此，本题还是有值得改进的地方．

(2016年浙江省数学高考文科试题第14题)

图4

图5

解法1(坐标法)如图5，设O为AC的中点，因为AB=BC，故BO⊥AC．以O为原点、AC所在直线为x轴建立空间直角坐标系O-xyz(如图5所示)．过点D′作D′E⊥AC于点E，D′F⊥平面ABD于点F，联结EF，则EF⊥AC，从而 ∠D′EF就是二面角D′-AC-D的平面角(设为α)．依题意

于是

设AC与BD′所成的角为θ，则

解法2(极端法)设二面角D′-AC-D为α．

于是

解得

图6

图7

2)如图7，当α=π时，点D′落在△ABC所在的平面内，设AC与BD′的延长线交于点E，DN⊥AC，BM⊥AC．由情形1)知

从而

在△BAD′中，由余弦定理求得BD′=2．又由情形1)知

根据△D′NE∽△BME得

解得

D′E=1.

因为CD′=1，故点E与C重合，即点D′在线段BC上，于是

点评本题考查2条异面直线所成的角，思路还是单一的，适合文科生．比较2015年理科第8题，也是翻折问题，该题用“极端法”解非常简捷，但本题用“极端法”解却并不显得轻松，相反，用“向量法”解运算量反而要小．“向量法”的难点在于如何建系，以及如何确定点D′的坐标．

例3如图8，在三棱台ABC-EDF中，已知平面BCFE⊥平面ABC，∠ACB=90°，BE=EF=FC=1，BC=2，AC=3．

1)求证：BF⊥平面ACDF；

2)求BD与平面ACFD所成角的余弦值．

(2016年浙江省数学高考文科试题第17题)

图8

图9

1)证法1(不补形法)如图9，在等腰梯形BCFE中，EF∥BC，BE=CF=1.设BC的中点为G，联结FG,则

FG=BE=1.

又BC=2，从而

于是△FGC是正三角形，故

∠BFG+∠CFG=90°，

即

BF⊥CF．

又平面BCFE⊥平面ABC，AC⊥BC，从而AC⊥平面BCFE，于是AC⊥BF，故BF⊥平面ACDF．

图10

证法2(补形法)如图10，由棱台的定义，分别延长AD,BE,CF交于一点P，因为EF∥BC且BE=EF=FC=1，BC=2，所以点E,F分别为PB,PC的中点，故△PBC是正三角形，于是BF⊥CF．又平面BCFE⊥平面ABC，AC⊥BC，从而AC⊥平面BCFE，于是AC⊥BF，故BF⊥平面ACDF．

2)解由第1)小题知BF⊥平面ACDF，从而∠BDF就是直线BD与平面ACFD所成的角．在Rt△BFD中，

于是

故

点评本题全省平均分为8.66，比命题预设的期望值要低一些．从阅卷反馈的信息来看，主要扣分点在于第1)小题的证明.学生用几何法的“三段论”书写证明过程时，推理论证不严谨，多数学生只能说出大概意思，想到用“补形法”的考生不多，主要是对棱台的定义不熟悉．第2)小题是以第1)小题的结论为基础，很容易找到“线面角”，计算也比较简单，故得分情况尚可．

例4如图8，在三棱台ABC-EDF中，已知平面BCFE⊥平面ABC，∠ACB=90°,BE=EF=CE=1,BC=2,AC=3．

1)求证：BF⊥平面ACDF；

2)求二面角B-AD-C的余弦值．

(2016年浙江省数学高考理科试题第17题)

点评本题第1)小题与文科完全一样，第2)小题的难度明显高于文科．下面对第2)小题进行探究.

2)解法1(几何法:补形)如图11，过点F作FH⊥AP于点H，联结BH．由第1)小题知BF⊥平面ACDF，从而BH⊥AP，于是∠BHF就是二面角B-AD-C的平面角．

在Rt△PAC中,

在Rt△PHF中,

在Rt△BHF中,

点评本解法有2个关键点:一是“补形”；二是找到二面角的平面角并证明,计算量并不大．虽然此法计算简捷，但是必须清晰棱台的定义才会想到补“台”为“锥”．

图11

图12

解法2(向量法:不补形法)如图12，过点F作FO⊥BC于点O，因为平面BCFE⊥平面ABC，所以FO⊥平面ABC．以O为原点、BC所在直线为x轴建立空间直角坐标系O-xyz．由题意得

从而

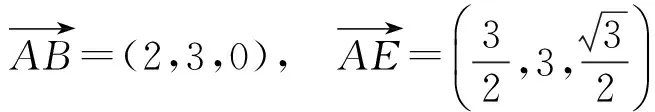
图13

点评本题的建系过程先证后建，近几年常考，这是考生容易失分的地方．本题建系的方案有多种，不同方案对计算的简捷与否有影响，能否选择恰当的方案是对学生能力的一种考量．用向量法，不补形也能解，对棱台定义模糊不清的学生,解题不受影响，这也是理科生本题得分尚可的原因之一，使得向量法作为一种“工具”的优势得到了充分的显现．

3　对教学的启示

毋庸置疑，高考命题对高中教学起着重要的导向作用．只有读懂命题专家是如何理解与把握“标准”的，才能对日常教学有正确的导向作用．

3.1严格按“标准”教学

所谓“标准”，即“课程标准”．何谓“标准”？华东师范大学崔允漷教授指出：“教育目的”的具体化是《课程标准》，而《课程标准》的具体化就是“学习目标”[1].可见，“标准”是课程育人目标的具体化．浙江省高中数学课程标准就是根据《国家高中数学课程标准》制订的《浙江省高中数学学科教学指导意见》．在实际教学实践过程中，许多教师对“课程标准”不够重视，或将“课程标准”束之高阁，或断章取义，或片面理解运用，最后导致了游离“课标”的教学行为的出现，使教学变得非常的随意，影响了学生的学习[2]．需要强调：“标准”是教师教学的“法”，执行“标准”关系到高中数学课程育人目标的落实，因此，教师教学必须守“法”，每节课教什么都要依据“标准”，不能急功近利，也不能仅凭经验．2016年立体几何解答题以三棱台为背景，学生平时接触较少，许多考生“卡壳”就卡在棱台的定义上，不知道将3条侧棱延长会相交于一点．由于近5年来高考没有考过棱台，因此师生们把棱台边缘化了．然而，我们来看一下《标准》的要求：了解棱柱、棱锥、棱台的底面、侧棱、侧面、顶点的意义；了解柱体、锥体、台体之间的关系[3]．不难看出，《标准》中对柱体、锥体、台体概念的要求是一样的，没有孰轻孰重．在文献[4]中专家指出：几何体中几何量的计算，其中包括角度、距离、面积、体积等．从问题分类来看，有证明题、计算题、探索题、判断题等；从图形的角度来分析，柱、锥、台、球及它们的组合体都成为考查的载体．由此可见，台体从未被排除在高考命题范围之外．因此，无论是平时教学还是高考复习，不应该把目光局限在考过的高考题型上，而必须基于“标准”，这才是“真教育”，才能真正做到对学生负责．

3.2重视“建系”方式的价值追问

建立恰当的直角坐标系，对于研究解析几何、立体几何至关重要，它将直接影响计算过程的简捷性．会根据实际问题情境建立合适的坐标系，不仅是一种能力，更是一种研究的素养．从高考阅卷的信息反馈看，学生在建立坐标系时花样百出，不少学生“左手系”和“右手系”都搞不清楚，高中阶段要求的是“右手系”；更多的是坐标系建得不合理，导致后面的运算复杂化．针对以上问题，反思我们的日常教学，平时对学生怎样建系的指导不够．建议平时教学中要加强对学生建系策略的指导，对于学生建好的系，要多追问：为什么要这样建系；有没有更好的建法，让学生在实践中感悟建立恰当的坐标系的意义和价值，提高数学素养．

3.3加强推理论证能力的培养

2016年的立体几何解答题，考生在推理论证方面暴露出的问题不少．原因既有基础原因，也有高中教学的原因．初中教育对平面几何推理论证要求的降低，使得学生运用“三段论”进行推理论证的能力显著下降；高中教师重思路、轻过程，对证明题过程书写要求不严，泛用向量法等，削弱了推理论证能力的培养．立体几何定理的学习既需要理解，也需要记忆，记住定理是运用定理的基础．但是，当下学生对几何定理记忆的意识和习惯比较差，许多学生到了高三仍对立体几何的基本定理说不清楚，谈何运用．因此，对立体几何定理教学在重视理解的同时，还要强化表述和记忆，特别是“三种语言”——文字语言、符号语言、图形语言之间的灵活转换．以笔者之见，文字语言有助于记忆，符号语言有助于推理过程的正确书写，图形语言有助于从复杂问题情境中提取定理的基本模型．要正确处理好几何法与向量法的运用关系，不能顾此失彼．在高三一轮复习时，要强调使用几何法，以巩固定理，规范证明过程书写，提高推理论证能力．在高三二轮复习时，要让学生根据实际，灵活选择几何法或向量法，实现简化解题过程之目的．

3.4提高画立体图的能力

画立体图是培养学生空间想象能力的有效途径．现在的立体几何教学，一般都是给出图形，不要求学生自己画图，故平时对学生画立体图的训练不够，有的学生甚至连什么时候画实线，什么时候画虚线都不知道．画立体图能力不强，会影响学生的空间想象，而空间想象又是数学要培养的核心素养之一．重视学生画立体图的训练，应当引起一线教师的足够重视．

总之，2016年的立体几何高考试题，粗看与往年的试题是“一样的风景”，但仔细琢磨，寓意深刻，无论是加强对“动态”情境问题的考查，还是变“柱”“锥”为“台”的微妙变化，无不在告诉一线教师日常教学要更加重视关注“标准”，更加重视关注核心素养．这不仅是专家的追求，也应该是一线教师的追求．

[1]崔允漷．有效教学[M]．上海：华东师范大学出版社，2009：110．

[2]翁洲．如何确定与叙写“学习目标”[J]．教育视界，2016(6)：16．

[3]浙江省基础教育课程改革专业指导委员会．浙江省高中数学学科教学指导意见[M]．杭州：浙江教育出版社，2014：15．

[4]高考数学研究组．浙江省数学高考数学2004一路走来[M]．杭州：浙江大学出版社，2016：127-157．

�2016-06-29；

2016-07-29

卢明(1961-)，男，浙江海盐人，浙江省特级教师.研究方向：数学教育．

O123.2

A

1003-6407(2016)10-26-06