基于改进Messinger覆冰模型导线防冰临界电流计算及其影响因素分析

刘国特 郝艳捧 阳 林 陈 彦 钟荣富



基于改进Messinger覆冰模型导线防冰临界电流计算及其影响因素分析

刘国特1,2郝艳捧1阳 林1陈 彦1钟荣富1

（1. 华南理工大学电力学院 广州 510640 2. 广东电网公司东莞供电局 东莞 523000）

为了得到不同覆冰气象条件下导线防冰临界电流，基于电流防冰时导线表面水膜流动，建立导线表面水膜流动模型对Messinger覆冰模型进行改进，确定了过冷水滴局部撞击系数（LCC）、导线表面局部对流换热系数（LHTC）与导线表面液态水局部冻结系数（LFC）计算方法。首次计算导线表面LHTC与LFC，并基于LFC计算结果，实现了导线防冰临界电流自动计算。计算结果表明：导线表面LCC、LHTC和LFC在导线驻点位置达到最大值，其中LFC随电流增大而减小；风速、温度是影响防冰临界电流的主要因素，含水量与水滴直径大小对临界电流没有明显影响。

导线覆冰 防冰 临界电流 局部撞击系数 局部冻结系数 控制体

0 引言

导线覆冰会造成输电线路断线、倒塔及导线舞动等事故，给电网安全稳定运行带来巨大威胁[1,2]。

目前，国内外所采用的热力除冰、机械除冰、自然脱冰等防冰、除冰方法中，电流热力防冰、除冰最具可行性[3-5]。但现有电流除冰在实施过程中需要融冰线路退出运行，这不仅会给电网和社会带来经济损失，还有可能威胁到电网的安全运行[6,7]。同时，附加融冰装置成本高、使用不方便，电源装置容量小，经常不能满足工程需求[8]。因此，在不断电、不增加融冰装置的前提下，通过增加导线的负荷电流，使其达到不覆冰时流过最小电流，即导线防冰临界电流，是最简单和有效的导线防冰方法。

目前，国内外导线防冰临界电流都是根据导线表面液态水的收集量和导线表面对流换热系数等经验公式建立能量平衡方程进行计算的[9-12]。这种计算方式忽略了导线表面局部撞击系数（Local Collision Coefficient，LCC）、局部对流换热系数（Local Heat Transfer Coefficient，LHTC）和导线表面水膜流动对能量平衡方程的影响。而在实际覆冰情况中，LCC和LHTC在导线表面变化很大[13-15]，而且随着导线电流增大，导线表面水膜流动产生的能量也越大，这些因素都会影响计算结果的准确性。

根据Makkonen覆冰模型，导线表面液态水收集系数与冻结系数决定了导线覆冰量，当冻结系数为0时，导线就不会覆冰[16]。因此，本文采用Fluent计算了导线周围的空气流场、导线表面压力和局部LHTC。使用拉格朗日法计算了覆冰过程中导线表面局部撞击系数，进而得到导线表面液态水局部收集系数。再将导线表面分为若干个控制体，建立导线表面水膜流动模型，对Messinger覆冰计算模型进行改进，计算出导线表面的局部冻结系数（Local Freezing Coefficient，LFC）。最后，把导线表面LFC都为0确定为防覆冰临界电流的数学条件，实现导线防冰临界电流的自动计算。

1 导线防覆冰电流计算

1.1 空气流场与导线表面局部对流换热系数计算

导线周围气流速度、导线表面压力和导线表面LHTC都是采用Fluent仿真得到，其空气流场计算运用k-epsilon模型，离散方程的数值求解采用Simple算法，具体过程参见文献[12]。

1.2 局部撞击系数计算

过冷水滴在导线表面的LCC决定了各控制体一个时间步长内收集的水量，对每个控制体的能量平衡和质量平衡计算起至关重要的作用，是临界电流计算的关键因素之一。本文根据牛顿第二定律，对单个过冷水滴进行受力分析，建立单个水滴的通用运动方程，采用传统的龙格库塔方法求解水滴运动微分方程就能得到水滴的运动轨迹，进而求得过冷水滴在导线表面的局部撞击系数，具体过程参见文献[17,18]。

1.3 Messinger覆冰模型改进方法

目前，所有覆冰计算模型都是基于Messinger覆冰模型进行开发的[19]，但Messinger模型对覆冰表面水膜流动过程处理比较简单，认为每个控制体未冻结的液态水全部流入下一个控制体中，没有考虑覆冰表面水膜流动对覆冰计算结果的影响，导致计算结果误差较大[20]。因此，本文对导线表面水膜运动过程进行了建模，并对其进行改进。

1.3.1 导线表面水膜流动模型

对每个控制体表面水膜而言，水膜具有厚度小、流动速度慢等特点。因此，可以忽略水膜表面张力，认为水膜以层流的形式在具有一定角度的平板上流动[21]，如图1所示，D为覆冰表面控制体长度。

图1 导线覆冰表面水膜流动模型

因此，导线表面水膜流动连续性方程为

水膜流动动量方程为

式中，为覆冰表面液态水密度。

冰层表面水膜流动采用速度无滑移边界，根据经典流体力学理论，冰面边界条件为

水膜表面动态边界条件为

对水膜表面进行法向和切向受力分析，根据受力平衡，得到水膜两个方向的动力学边界条件为

式中，为水膜控制体中心压力；0为气流场压力；为水膜运动粘度，取=1.78×10-6m2/s；为水膜厚度；h为第个控制体水膜厚度。根据水膜连续方程、动量方程与边界条件即可求出每个控制体的水膜厚度与水膜速度。

1.3.2 改进后的Messengers覆冰模型

Messinger覆冰计算模型包含覆冰质量守恒和覆冰能量守恒两部分[13]，表达式为

式中，ice为结冰质量；im为过冷水滴撞击控制体带来的水的质量，且

当前控制体流出水的质量out为

式中，w为水膜密度；为水膜速度。

周围控制体流入当前控制体的水的质量in为

蒸发或升华产生的水蒸气的质量[22]evap为

式中，c为覆冰表面局部传热系数；v为水蒸气的气体常数，取v=461.1J/kg；s为该控制体来自外界饱和水蒸气压力；ss为覆冰控制体表面压力；s、w分别为覆冰控制体的表面温度和来流温度；为相对湿度，此处 =98%；a为空气密度；a为空气的比热容；a定义为Lewis数，a=1。

液态水结冰需要消耗的能量[13]ice为

式中，f为水的凝结潜热。

对于雾淞覆冰，冰升华的能量[14]evap为

式中，s为冰的升华潜热；e为水的汽化潜热；w为水的比热容；s为控制体平衡温度；0为结冰温度，0=273.15K。

气流摩擦覆冰表面产生的热能[15]f为

式中，为覆冰控制体表面面积；c为附面层恢复系数。

热传导的热流[15]k为

对流传热[15]c为

防覆冰电流产生的热量[23]r为

式中，为导线直径；ac,Ts为导线温度s时的交流电阻，由于趋肤效应影响，电流主要分布在导线表面，导致ac,Ts增大，其表达式为[12]

式中，为趋肤效应系数；20为导线电阻温度系数。

撞击在当前控制体的过冷水滴能量[15]im为

out为流出当前控制单元溢流水的能量，in为流入当前控制单元溢流水的能量[24]，其表达式分别为

式中，in为流入控制体液态水速度方向与水平轴的角度；out为流出控制体液态水速度方向与水平轴的角度。

根据每个控制体的质量守恒，可以得到该控制体的冻结系数[20]为

当冻结系数为0时，该控制体不会结冰。

2 计算结果与分析

为了研究导线周围流场计算参数见表1[10]，采用Fluent流体力学仿真软件计算了导线周围空气流场计算结果，如图2所示，提取导线表面LHTC，如图3所示，使用拉格朗日法计算过冷水滴运动轨迹与水滴在导线表面的LCC，如图4所示，并通过式（22），得到LGJ—240130型号导线表面LWC=0.2g/m3，MVD=40mm时LFC随导线运行电流的变化情况，如图5所示。当导线表面LFC为0时的导线运行电流为防冰临界电流。

表1 流场计算参数

Tab.1 Calculation parameters of flow field

图2 导线周围空气流场计算结果

2.1 空气流场计算结果

当气流从远处向导线流动时，由于静压的阻碍作用，气流速度逐渐降低，在迎风面驻点附近位置，气流速度达到最小值。然后，气流速度沿着导线上下表面迅速增大并达到最大值，随后，气流速度又逐渐减小。

2.2 LHTC计算结果

导线迎风面附近，气流速度大的位置雷诺数越大，相应导线附近温度层变薄，导致其湍流边界层导热热阻的导热系数增大，导热热阻减小，降低了导线表面的局部对流换热系数。所以，LHTC在驻点位置最大，然后随着||的增大，逐渐减小（见图3）。

图3 导线表面迎风面LHTC

2.3 LCC计算结果

由于导线附近静压与速度成反比，所以，导线前缘驻点位置静压比较小，其附近过冷水滴在导线前缘速度降低、梯度较小，导致此处过冷水滴具有较大的动量，难以偏离运动轨迹，所以有更多的水滴撞击在此处。随着||的增大，导线附近静压减小，水滴速度降低梯度较大，所以过冷水滴动量降低较大[24]，过冷水滴容易偏离运动轨迹（见图4a）。因此，LCC在迎风面的驻点位置处为最大值，然后随着||的增大，逐渐减小（见图4b）。

（a）过冷水滴运动轨迹

（b）导线表面迎风面局部撞击系数

图4 导线表面迎风面局部撞击系数

Fig.4 LCC distribution around windward surface of the conductor

2.4 局部冻结系数与电流关系

导线表面水膜在气流剪切力与自身重力作用下，在导线表面流动。随电流的增大，导线产生的焦耳热增多，使各控制体的覆冰冻结量减小，也增加了水膜流动产生的热量。因此，随着电流的增大，LFC减小。当导线表面液态水冻结系数为0时，导线运行电流为486.42A时，为防冰临界电流（见图5）。

2.5 模型比较

根据文献[11]的实验参数，见表2，计算了导线的防冰临界电流。本文计算结果与实验结果误差在5%之内，比文献[10-12]计算结果更加准确。结果如图6所示。

表2 文献[11]实验参数

Tab.2 Test parameters of Ref.[11]

图6 计算值与实验值及文献[10-12]模型比较

3 防冰临界电流影响因素分析

导线防覆冰临界电流与风速、空气中液态水含量、温度及过冷水滴直径等因素密切相关。本文选用导线LGJ—240/30分析覆冰微气象因素与导线防覆冰临界电流的关系。

3.1 风速对防覆冰电流的影响

随风速的增大，导线表面LHTC迅速增大，导致对流传热损耗的能量增加。而气流摩擦、过冷水滴撞击和水膜流动产生的能量在风速较低时增加不明显，但在风速较高时增加较快。因此，防冰临界电流先随风速增大而迅速增大，然后，逐渐趋向于平缓，由此可得LWC=0.5g/m3，MVD=50mm时，临界电流与风速关系如图7所示。

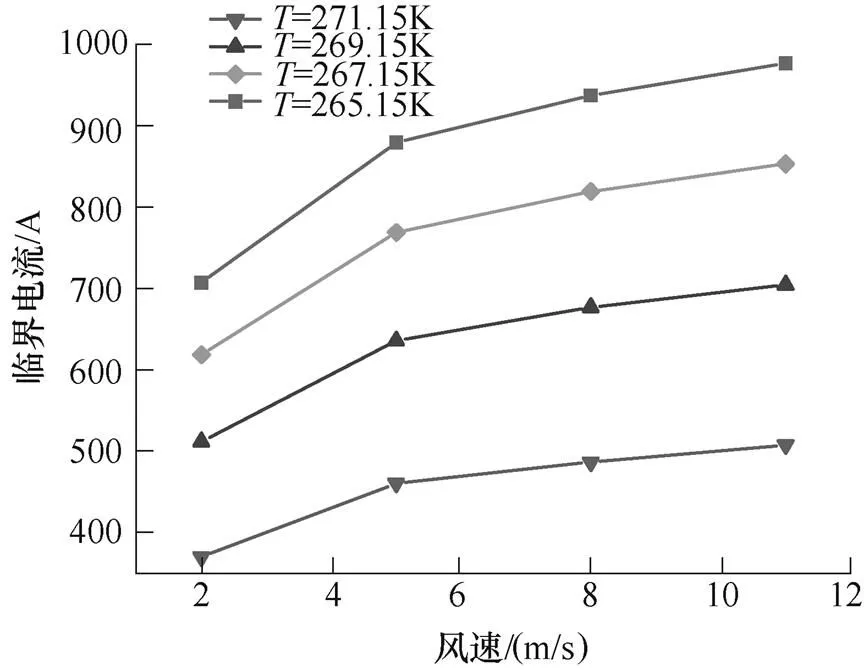
图7 临界电流与风速关系

3.2 温度对防覆冰电流的影响

随环境温度的降低，热传导损失的能量增多。同时，由于空气中过冷却水滴温度与周围环境温度相同，其撞在导线上的过冷水滴液态水从环境温度上升到导线表面温度也需要消耗一部分能量。而且，导线表面水膜流动产生的热量减小。因此，当LWC= 0.5g/m3，MVD=20mm时随着温度降低，防冰临界电流增大，临界电流与温度关系曲线如图8所示。

图8 临界电流与温度关系

3.3 含水量对防覆冰电流的影响

随含水量的增大，导线表面液态水收集系数增大，过冷却水滴撞击导线和导线表面水膜流动产生的热量增加，但撞击在导线表面上的液态水从环境温度上升到导线表面温度需要消耗更多能量。因此，当LWC=8g/m3，MVD=50mm时，随含水量的增大，防冰临界电流相应增大，临界电流与含水量关系曲线如图9所示。

图9 临界电流与含水量关系

3.4 过冷水滴直径对防覆冰电流的影响

随着水滴直径的增大，导线表面LCC增大，并在水滴直径为50mm时趋向饱和。因此，临界电流随水滴直径的增大而增大，并在水滴直径为50mm时，趋向饱和。当LWC=0.5g/m3，=270.15K时，临界电流与水滴直径关系曲线如图10所示。

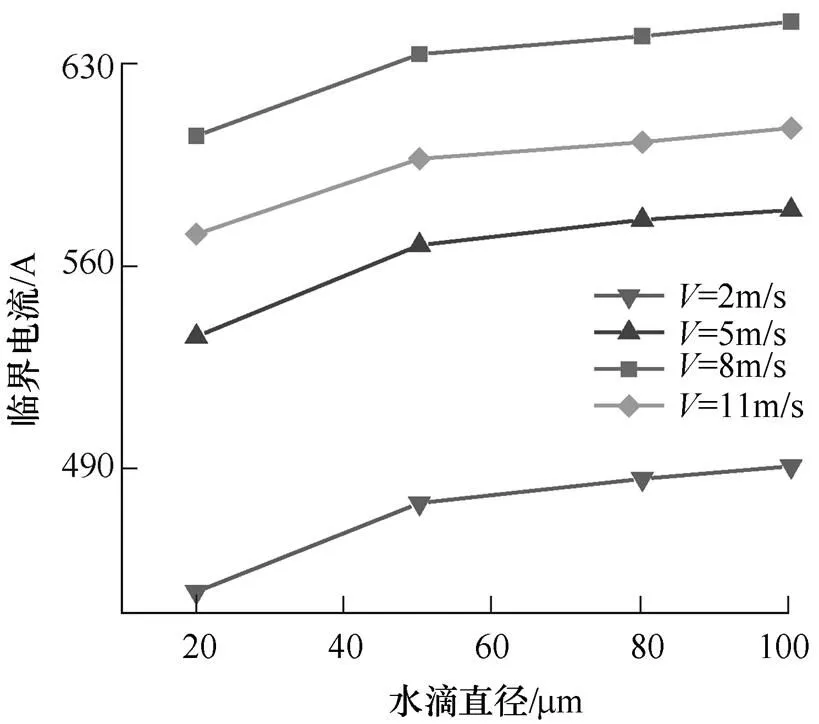
图10 临界电流与水滴直径关系

4 结论

本文基于改进Messinger覆冰模型，根据导线覆冰增长过程的实际情况，确定了导线表面LHTC、LFC计算方法，首次计算了导线表面的LHTC和LFC，揭示了导线表面LHTC和LFC的规律。并首次根据导线表面液态水的LFC，对导线防冰临界电流进行了研究，得到以下结论：

1）LHTC和LFC在驻点位置达到最大值，然后沿着导线上、下表面逐渐减小。

2）导线运行电流产生的焦耳热能有效降低导线表面液态水的LFC，随电流的增大，导线表面液态水LFC降低。

3）风速、环境温度是影响导线防覆冰临界电流的主要因素，含水量与水滴直径大小对临界电流没有明显影响，当过冷水滴直径大于50mm时，防冰临界电流趋向饱和。

参考文献

[1] 肖良成, 李新民, 江俊. 四分裂新月形覆冰导线的气动扰流特性分析[J]. 电工技术学报, 2014, 29(12): 261-268.

Xiao Liangcheng, Li Xinmin, Jiang Jun. Study on aerodynamic characteristics of quad-bundled crescent- shape iced-conductors[J]. Transactions of China Electrotechnical Society, 2014, 29(12): 261-268.

[2] 张志劲, 黄海舟, 蒋兴良, 等. 复合绝缘子雾凇覆冰厚度预测模型[J]. 电工技术学报, 2014, 29(6): 318-326.

Zhang Zhijin, Huang Haizhou, Jiang Xingliang, et al. Model for predicting thickness of rime accreted on composite insulators[J]. Transactions of China Electro- technical Society, 2014, 29(6): 318-326.

[3] 许俊, 郭耀杰, 曹珂, 等. 考虑多档导线及绝缘子串影响的覆冰及脱冰输电导线找形分析[J]. 电工技术学报, 2015, 30(13): 87-91.

Xu Jun, Guo Yaojie, Cao Ke，et al. Research on form-finding of icing and ice-shedding transmission line considering the influence of multi-span and insulator string[J]. Transactions of China Electro- technical Society, 2015, 30(13): 87-91.

[4] Peter Z, Volat C, Farzaneh M, et al. Numerical investigations of a new thermal de-icing method for overhead conductors based on high current impu- lses[J]. IET Generation, Transmission& Distribution, 2008, 2(5): 666-675.

[5] Zhang Guixin, Chen Sheng, Xu Shuguang, et al. Application and research of laser de-icing in power system[C]// IEEE International on Power Modulator and High Voltage Conference (IPMHVC), Atlanta, GA, 2010: 470-473.

[6] 王艳, 杜志叶, 阮江军. 高压架空输电线路覆冰情况下风险评估研究[J]. 电力系统保护与控制, 2016, 44(10): 84-90.

Wang Yan, Du Zhiye, Ruan Jiangjun. Reliability risk evaluation for the high voltage overhead transmission line under icing condition[J]. Power System Pro- tection and Control, 2016, 44(10): 84-90.

[7] Liu Gang, Hui Peng, Lehtonen M, et al. De-icing schemes and operations for overhead power line based on shunt capacitor over-compensation method[C]// International Conference on Electrical and Control Engineering (ICECE), Wuhan, 2010: 3525-3528.

[8] 许树楷, 赵杰. 电网冰灾案例及抗冰融冰技术综述[J]. 南方电网技术, 2008, 2(2): 1-2.

Xu Shukai, Zhao Jie. Summarize the ice disaster accidents and its anti-icing technology in power system[J]. Southward Power System Technology, 2008, 2(2): 1-2.

[9] 刘和云, 周迪. 防止导线覆冰临界电流的传热研究[J].中国电力, 2001, 34(3): 12-16.

Liu Heyun, Zhou Di. Heat transfer investigation on critical current to prevent wires from icing[J]. China Electric Power, 2001, 34(3): 12-16.

[10] Personne P. Ice accretion on wires and anti-icing induced by joule effect[J]. Journal of Applied Meteorology, 1998, 27(2): 104-114.

[11] 蒋兴良, 兰强, 毕茂强. 导线临界防冰电流及其影响因素分析[J]. 高电压技术, 2012, 38(5): 1225- 1232.

Jiang Xingliang, Lan Qiang, Bi Maoqiang. Analysis on critical anti-icing current of conductor and its impacting factors[J]. High Voltage Engineering, 2012, 38(5): 1225-1232.

[12] Peter Z. Modelling and simulation of the ice melting process on a current-carrying electrical conductor[D]. Quebec: Quebec University, 2006.

[13] 常士楠, 袁美名, 霍西恒, 等. 某型飞机机翼防冰系统计算分析[J]. 航空动力学报, 2008, 23(6): 1141-1145.

Chang Shinan, Yuan Meiming, Huo Xiheng, et al. Investigations of the bleed air anti-icing system for an aircraft wing[J]. Journal of Aerospace Power, 2008, 23(6): 1141-1145

[14] 卜雪琴, 林贵平, 彭又新, 等. 防冰热载荷计算的一种新方法[J]. 航空学报, 2006, 27(2): 208-212.

Bu Xueqin, Lin Guiping, Peng Youxin, et al. New method for calculation of anti-icing heat loads[J]. Acta Aeronautica at Astrouantics Sinic, 2006, 27(2): 208-212.

[15] 赵勇, 杨新亮. 飞机水平尾翼水滴撞击特性及防冰热荷载计算[J]. 航空动力学报, 2012, 27(11): 2041-2047.

Zhao Yong, Yang Xinliang. Impingement characteri- stics and anti-icing heat load calculation of certain tail-plane[J]. Journal of Aerospace Power, 2012, 27(11): 2041-2047.

[16] Makkonen L. Modeling power line icing in freezing precipitation[J]. Atmospheric Research, 1998, 46(s1-2): 131-142.

[17] Thomas S, Cassoni R. Aircraft anti-icing and de-icing techniques and modeling[J]. Journal of Aircraft, 1996, 33(5): 841-854.

[18] Caruso S. LEWICE droplet trajectory calculations on a parallel computer[R]. American Institute of Aeronautics and Astronautics, 1993.

[19] Myers T G, Charpin J P F, Thompson C P. Slowly accretion ice due to supercooled water impacting on a cold surface[J]. Physics of Fluids, 2002, 14(1): 240- 256.

[20] Bourgault Y, habashi W G, Beaugendre H. Develop- ment of a shallow water icing model in FENSAP- ICE[R]. AIAA-99-0246, 1999.

[21] Myers T G, Charpin J P F, Chapman S J. The flow and solidification of a thin fluid film on an arbitrary three-dimensional surface[J]. Physics of Fluids, 2001, 14(8): 2788-2803.

[22] Wright W B. User manual for the NASA Glenn ice accretion code LEWICE version 2.2.2[R]. NASA- CR_2002-211793, 2002.

[23] Ping Fu. Modeling and simulation of the ice accretion process on fixed or rotating cylindrical objects by the boundary element method[D]. Quebec: Quebec University, 2004.

[24] Bourgault Y, Boutanios Z, Habashi W G. Three- dimensional eulerian approach to droplet impinge- ment simulation using FENSAP-ICE, part 1: model algorithm and validation[J]. Journal of Aircraft, 2000, 37(1): 95-103.

Caculation and Influencing Factors Analysis of Conductor Anti-Icing Critical Current Based on Improved Messinger Icing Model

1,21111

（1. School of Electric Power South China University of Technology Guangzhou 510640 China 2. Dongguan Power Supply Bureau Guangdong Power Grid Corporation Dongguan 523000 China）

This paper improves the Messinger icing model by establishing the water film flow model on conductor surface based on the water film flowing on conductor surface during the current anti-icing periods, to obtain the conductor anti-icing critical current under different icing meteorological conditions. The calculation methods about the local collision coefficient (LCC) of super-cooled water droplets, the local heat transfer coefficient (LHTC) on conductor surface and the local freezing coefficient (LFC) of liquid water on conductor surface are determined. It is the first time to calculate the LHTC and LFC on conductor surface. Moreover, the automatic computation of conductor anti-icing critical current is achieved based on the calculated LFC. The results show that the LCC, LHTC and LFC on conductor surface reach their maximum values in the position of conductor stagnation point, where the LFC decreases with increasing the conductor current. Wind speed and temperature are the main factors affecting the anti-icing critical current, while the water content and the diameter size of droplet have little effects on the critical current.

Conductor icing, anti-icing, critical current, local collision coefficient, local freezing coefficient, control body

TM216

刘国特 男，1979年生，博士研究生，研究方向为输变电设备外绝缘。

E-mail: liuguote@sohu.com（通信作者）

郝艳捧 女，1974年生，教授，博士生导师，研究方向为关键电力设备绝缘状态诊断、电力系统过电压及其防护、大气压介质阻挡放电等。

E-mail: yphao@scut.edu.cn

2014-08-18 改稿日期 2014-11-10

国家高科技研究发展计划（863计划）（2011AA05A120）和国家自然科学基金面上项目（51177052）资助。