交易对手信用风险管理的实证分析

喻 平，于雪皎,2



交易对手信用风险管理的实证分析

喻 平1，于雪皎1,2

（1.武汉理工大学经济学院，武汉 430070；2.Durham University, Durham DH1 3LE, UK）

在近年来的金融危机中，参与场外衍生品交易而引起的信用违约事件对整个金融体系冲击很大，因此防范交易对手信用风险尤为重要。本文基于构建的金融衍生品资产组合，根据t-Copula函数的拟合结果研究汇率与利率之间的相关性，再结合资产组合的盈亏情况研究市场风险的变动对交易对手信用风险暴露的影响。最后，基于全文实证分析结果提出通过转换结算方式、注重风险缓释措施、引入交易结算对手等措施来加强对金融风险之间相关性的防范。

交易对手信用风险；Copula函数；风险暴露

一、引言

信用风险是金融系统面临的最主要的风险之一，一般是指债务人在债务到期时，不想或者无法偿还债务而给债权人造成损失的可能性。其成因除了债务人的故意违约之外，大多是受信用活动中的不确定性影响。不确定性在金融市场中是必然存在的，但如果和风险并存，通常就是负面结果，因此信用风险通常也是负面结果[1]。交易对手信用风险是传统信用风险分化出来的一个特殊风险，是指由于借款人或交易对手不能或不愿履行合约而给另一方带来损失的可能性。交易对手选择达成一项协议的出发点通常是为了规避市场波动给资产带来的风险，所以其风险主要由市场风险产生，但由于最终的结果往往表现为履约的失败，所以会表现为信用风险。

2008年美国次贷危机爆发后[2]，金融市场上一系列交易活跃的衍生品纷纷出现了违约的现象，由于各个金融机构和衍生品交易市场间都存在一定的关联交易，因此金融危机使得交易对手的信用风险逐渐暴露出来，同时违约金额的成倍增加也助推了市场的波动，最终使风险在全球迅速蔓延。巴塞尔委员会为了严格控制风险范围的扩散，降低风险的影响，防止在未来经济周期中不断爆发新的危机，颁布了《巴塞尔协议Ⅲ》，对金融机构在控制交易对手信用风险方面提出了更加严格的要求，同时也提出了一些具体改革方案。各大金融机构也纷纷拓展金融衍生品业务，给金融市场提供更多用来规避风险的产品。但在金融创新的同时，也不可避免会产生新的不确定性和风险，尤其当市场风险不可避免时，即使交易合约能够顺利履行，但仍会产生一定的亏损。通常在合约交割日时，如果合约仍具有正向收益，那么合约持有人会选择履行合约进行交割，相反，如果合约出现亏损，那么合约持有人就可能会选择不履行合约。由于合约的实际盈亏情况与金融市场的变动紧密相关，因此在探讨交易对手信用风险的成因及对策时，不但要考虑交易对手自身的信用状况，更要结合市场风险因素。

本文根据境内金融市场的实际情况构建了金融衍生品虚拟资产组合，研究市场风险的变动对交易对手信用风险暴露的影响。由于市场风险的成因多种多样，本文只选择利率和汇率两种市场风险，先采用t-Copula函数证明利率风险和汇率风险之间存在相关性，说明不同市场风险因素之间的相关性会引起交易对手信用风险的变化[3]。再对Copula函数在金融领域的扩展进行说明，最终提出应对交易对手信用风险的建议。

二、文献回顾

（一）交易对手信用风险文献回顾

巴塞尔委员会于1986年最早提出交易对手信用风险的概念，认为金融衍生产品存在的信用风险最终会由其交易对手承担。Canabarro和Duffie指出交易对手信用风险与其他信用风险的相似之处在于都是由于债务人的违约而出现了经济损失，但与传统的信用风险的两个不同点在于风险暴露的不确定性和信用风险的双边性[4]。Michale S. Gibon研究了引入保证金对于降低交易对手信用风险的作用①，认为保证金能够大大降低信用风险的暴露值，预期降幅达80%，之后将保证金期限因素引入模型中，来增加测算风险暴露值的准确性。Lomibao.D和S.Zhu提出了用来简化路径依赖方法（Path-dependent）的条件计量方法[5]。Michael Pykhtin和Steven H. Zhu阐述了交易对手信用风险暴露的特征[6]，并分别计算了交易对手风险暴露和传统交易合约固有风险暴露的大小，利用PDS模型给出了交易对手风险定价方法，为风险暴露的建模提供了思路，分析了交易对手独立性对风险暴露关联性的影响。Michael Pykhtin和Dan Rosen提出了针对不同交易水平和信用价值调整（CVA）的交易对手信用风险计量方法[7]，同时还提出了一个新模型用来衡量交易对手双边抵押品对于预期风险暴露的影响，并剔除了相似预期暴露的关联性。Jon Gregory认为交易对手信用风险只能降低不能完全消除[8]，所以要重视缩小风险暴露的方法，并将存在抵押品和不存在抵押品两种情况进行了量化对比，提出要通过增加抵押品的比重来防范交易对手信用风险。

（二）Copula函数文献回顾

Sklar第一次提出了Copula函数，表明一个k元联合分布可以分解成K个边缘分布函数和一个Copula 函数，而这个Copula函数刚好能够描述各变量之间的相关性[9]。Embrechts第一次把 Copula函数引进到了金融领域[10]，引入了Copula函数作为新的相依性度量的手段。Patton将 Copula 函数应用于美元对马克、日元汇率的实证研究中②，进一步验证了 Copula 函数能更好地对金融市场间的相关性进行描述。Rockinger和Jondeau建立了Copula-GARCH模型③，动态地对不同股票市场收益率之间的相关性进行研究，并发现t-Copula函数能较好地描述金融变量之间的相关性。Hu， Kiesel和Perraudin利用线性组合多个Copula函数的方式构造得到了混合Copula函数[11]，能对金融市场间复杂的相关结构描述更准确，并用不同的系数描述不同的相关性结构。国内对Copula 理论的研究起步较晚，而且主要是集中在实证方面的探讨。张尧庭最先引入并介绍了Copula函数[12]，从理论上证明了 Copula 函数在金融研究中的可行性。侯成琪和王频构建了针对不同风险类型的Copula-风险价值模型[13]，并给出了蒙特卡洛模拟算法。陈希镇和胡兆红提出以分布图像拟合检验和最短距离法来寻找最优Copula函数[14]，同时通过GARCH模型改进了传统的求风险价值的蒙特卡洛模拟法。近年来，学者对Copula函数的研究逐渐加深，但对Copula函数在金融衍生品估值和交易对手风险管理上的研究还不够深入，尤其是结合中国金融市场实际情况的研究还非常少。同时，Copula函数在风险管理方面的研究大多集中在资产收益率的相关性上，较少研究风险因素的相关性[15]。

三、交易对手信用风险暴露的实证分析

选择境内金融市场上两类主要的金融衍生品：外汇远期和利率掉期，基于美元对人民币汇率、美元利率、人民币利率三类市场风险因素，采用现期风险暴露法计量两类金融衍生品的风险暴露[3]。

（一）资产组合与市场数据的选择

1.构建资产组合

由于境内的商业银行普遍提供的是一年期内的金融衍生品交易，并且短期的衍生品具有更好的流动性，所以此次构建的资产组合以短期金融衍生品为研究目标，选取了外汇远期合约和利率互换合约。市场上短期限的外汇远期和利率互换的流动性较好，再加之中国目前推出的外汇远期和利率互换业务也都以一年期内的短期为主，剩余期限为5年或7年的金融衍生产品流动性较差，所以此次只选择一年期内的衍生产品进行资产组合。其中，外汇远期和美元利率掉的名义本金都设定为100万美元，人民币利率掉期的名义本金设定为100万人民币。美元利率采用LIBOR O/N，人民币利率将采用更贴近市场变动情况的SHIBOR O/N该资产组合共涉及到美元对人民币汇率[16]、美元利率、人民币利率三类风险，具体的资产组合情况如下表所示④。

表1：资产组合中衍生产品的信息

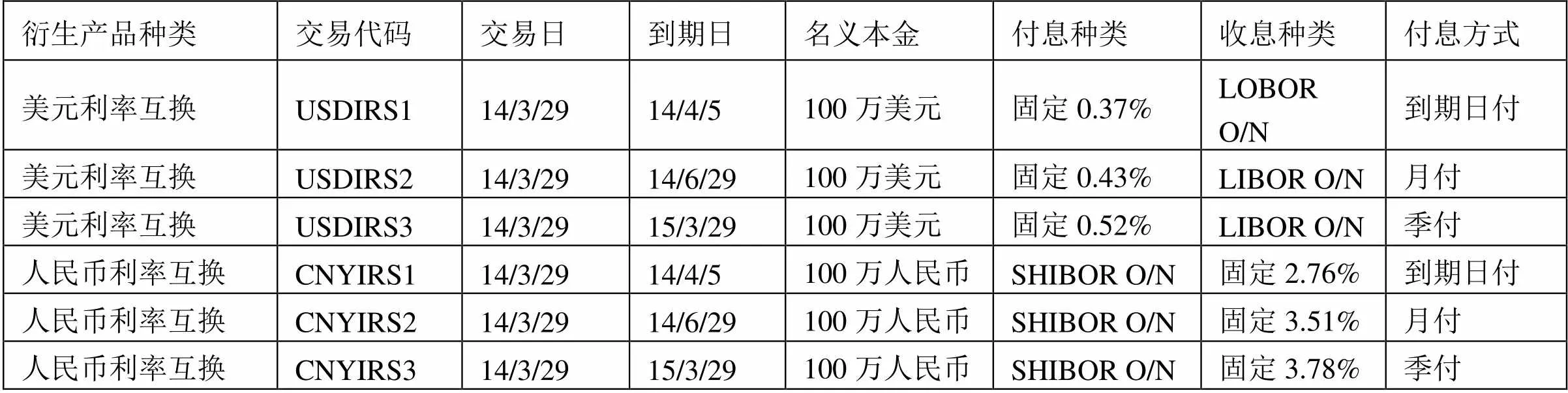
表2：资产组合中衍生产品信息⑤

2.选择市场数据

2010 年 6 月，中国人民银行启动了“二次汇改”，人民币继续快速升值，自2011 年下半年开始，人民币单边升值的趋势彻底改变，汇率市场双边波动的倾向越来越明显。为了验证国内市场美元对人民币汇率、美元利率、人民币利率之间是否存在一定联系，本文选取了2013年1月4日至2015年4月4日的美元对人民币汇率中间价⑥、LIBOR美元利率、SHIBOR人民币利率用于分析相关性并计算交易对手信用风险的暴露值。

（二）交易对手信用风险敞口的计量-基于现期风险暴露法

现期风险暴露法的优点主要在于简单方便，不需要对未来的风险暴露进行模拟，时间跨度可以调控，计算量小，易于实施；不足之处主要在于其对市场风险因素的变化不能作出及时的反应，且计算的风险暴露往往过于保守，不能及时地将金融市场的变化反映在风险暴露中。

现期风险暴露值=以公允价值计算的重置成本+名义本金×固定系数

其中，重置成本是金融衍生产品的市场价值与0的最大值。因为如果交易对手违约，当交易对手金融衍生品的价值为正时，商业银行从市场上获得相同头寸的成本为当前金融衍生品的价值，因此重置成本即为当前金融衍生品的价值；金融衍生品的价值为负时，商业银行从市场上获得相同头寸的成本为0，因此重置成本也为0。固定系数由巴塞尔协议统一规定，一年期内利率的固定系数为0.0%，一年期内汇率的固定系数为1.0%。

1.计算估值的原理

（1）汇率互换的估值要先将远端处的两笔外汇资产在远期汇率下进行扎差，再进行折现。

（2）利率互换的估值要借鉴一般利率互换价值估量的基本方法-债券组合分解法[17]。由于利率互换协议签订生效时刻交易双方均没有发生现金流量，因此利率互换的价值实际上是固定利率债券价值与浮动利率债券价值的差。

假设利率互换协议的名义本金为L，距离协议到期日还要付息n次，固定利率为R，公允价值为Vswap，固定利率债券的价值为Vfix，浮动利率债券的价值为Vfloat，那么利率互换协议的实际公允价值为

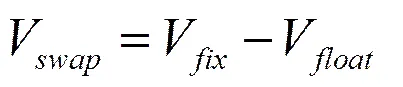
设ti为利率互换协议生效日至第i次现金流交换的时间（1≤i≤n），ri为ti当日的SHIBOR/LIBOR利率，则

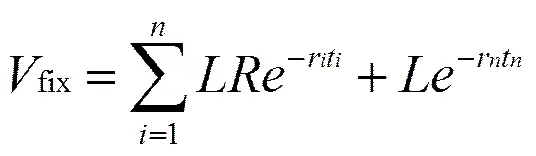
根据浮动利率债券的性质，假设利息下一支付日应支付的人民币浮动利息额为I，那么在ti日的浮动利率债券的价值为L+I，则

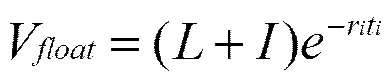
此时，利率互换的当前公允价值估计量为

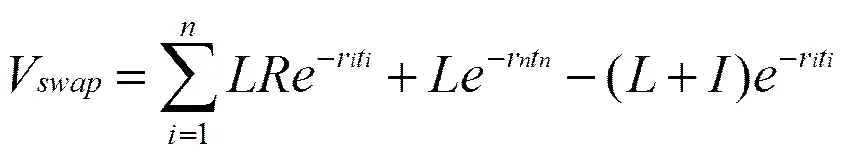
2.计算结果

将表2中的美元固定利率、LIOBR O/N、人民币固定利率、SHIBOR O/N分别带入公式（4）中[18]，即可得到表3的结果。

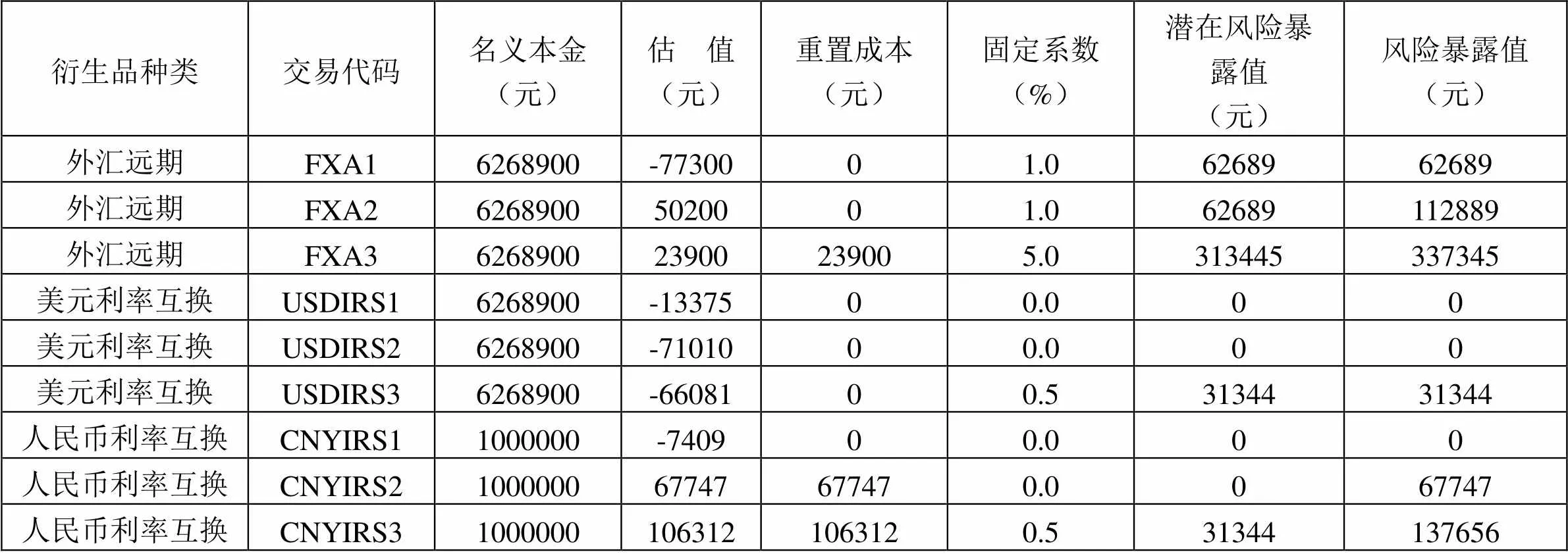
表3：交易对手现期信用风险暴露值

从整个金融衍生品资产组合来看，当前的风险暴露值为749670元。如果在加入汇率与利率之间的相关性因素之后风险暴露值增加或减小，则证明市场风险之间的相关性对交易对手信用风险有影响；如果加入汇率与利率之间的相关性因素之后风险暴露值近似不变，则证明市场风险之间的相关性对交易对手信用风险没有影响。

四、相关性对交易对手信用风险影响的实证分析

用2013年1月4日至2015年4月4日的美元对人民币汇率、LIBOR O/N、SHIBOR O/N共1689个数据研究美元对人民币汇率与美元利率和美元对人民币利率与人民币利率之间的相关性，并分别构建二元Copula函数来描述美元对人民币汇率与美元利率、美元对人民币汇率与人民币利率之间的相关结构[19]。

（一）基于Copula函数的相关性分析

1.数据描述

图1：USD/CNY的频率直方图

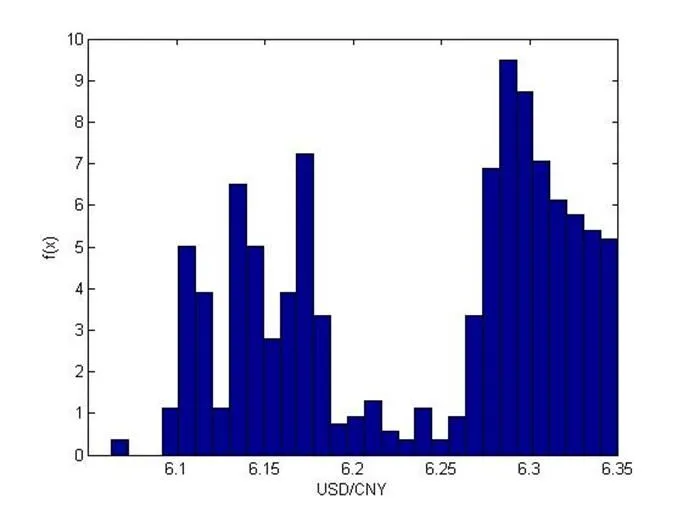
图2：LIBOR的频率直方图

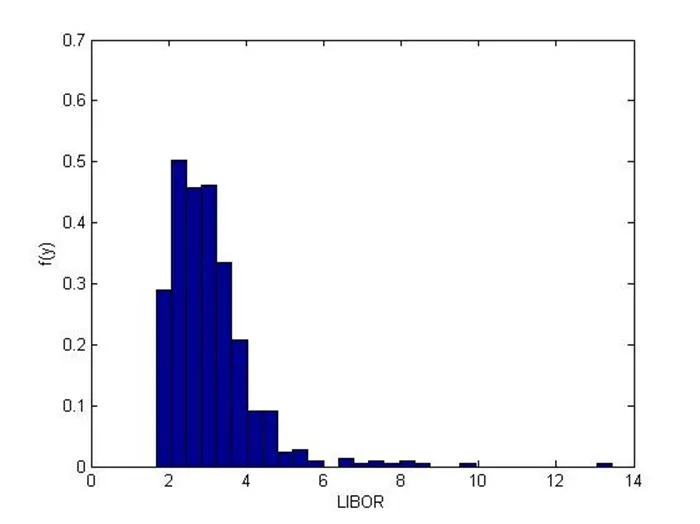
图3：SHIBOR的频率直方图

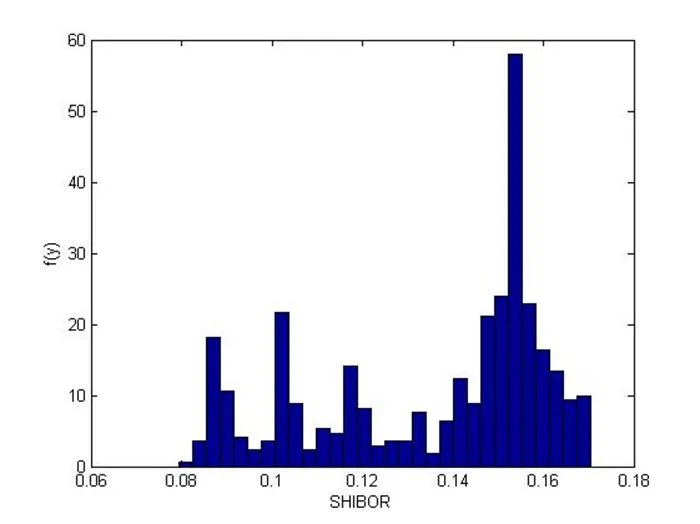
本文全部利用MATLAB软件进行相关分析。令USD/CNY表示美元对人民币汇率，LIBOR表示美元利率，SHIBOR表示人民币利率。分别做出USD/CNY、LIBOR、SHIBOR的分布直方图（图1、图2、图3），根据软件计量结果显示（见表4），USD/CNY右偏且比正态分布平缓，LIBOR左偏且比正态分布陡峭，SHIBOR右偏且比正态分布平缓，三个变量均不属于正态分布，不能用参数法对Copula函数进行参数估计[7]。

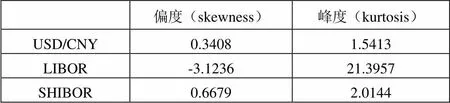
表4：变量统计指标

2.确定边缘分布

采用非参数法确定两个随机变量的分布情况，并画出各自的经验分布函数图和核分布估计图（图4、图5、图6）。

图4：USD/CNY的分布图

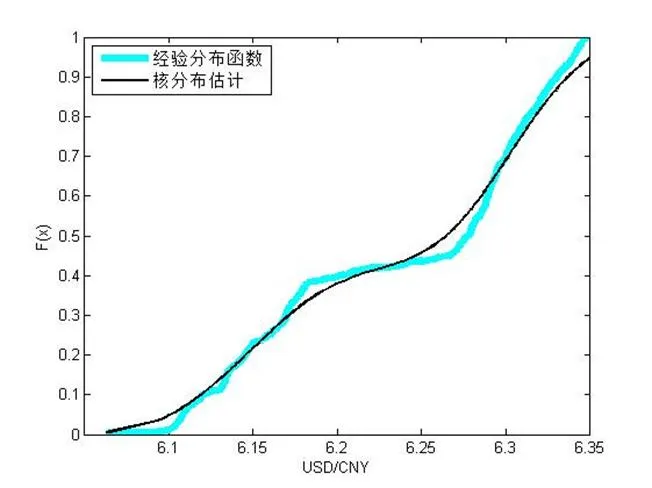
图5：LIBOR的分布图

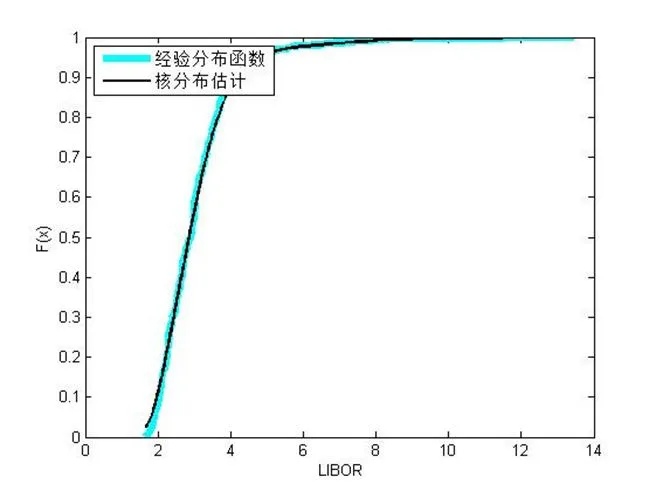
图6：SHIBOR的分布图

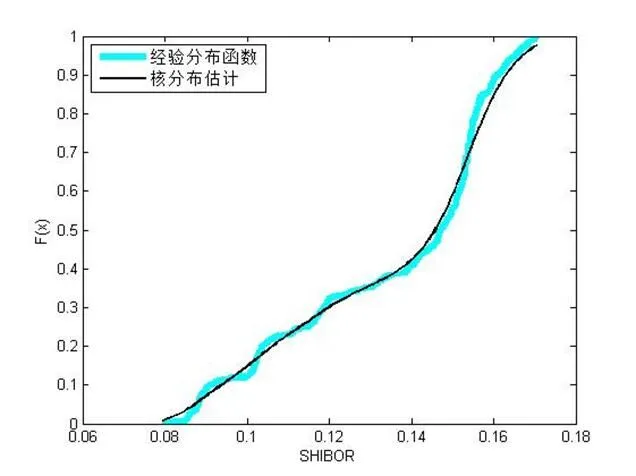
3.Copula函数的选择与参数的估计

（1）Copula函数的选择

在上文中确定了USD/CNY的边缘函数U（x）和LIBOR的边缘函数V1（x）及SHIBOR的边缘函数V2（x）之后，先绘制（U，V）的二元频数直方图（图7、图9），再根据频数直方图绘制出频率直方图（图8、图10），根据频率直方图的形状能够更好的判定合适的Copula函数[20]。

图7：USD/CNY和LIBOR的联合频数直方图

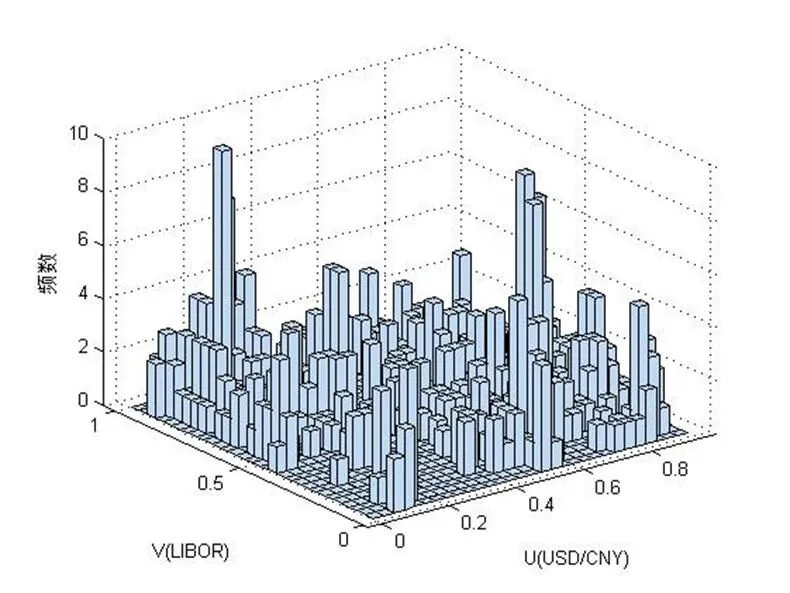
图8：USD/CNY和LIBOR的联合频率分布直方图

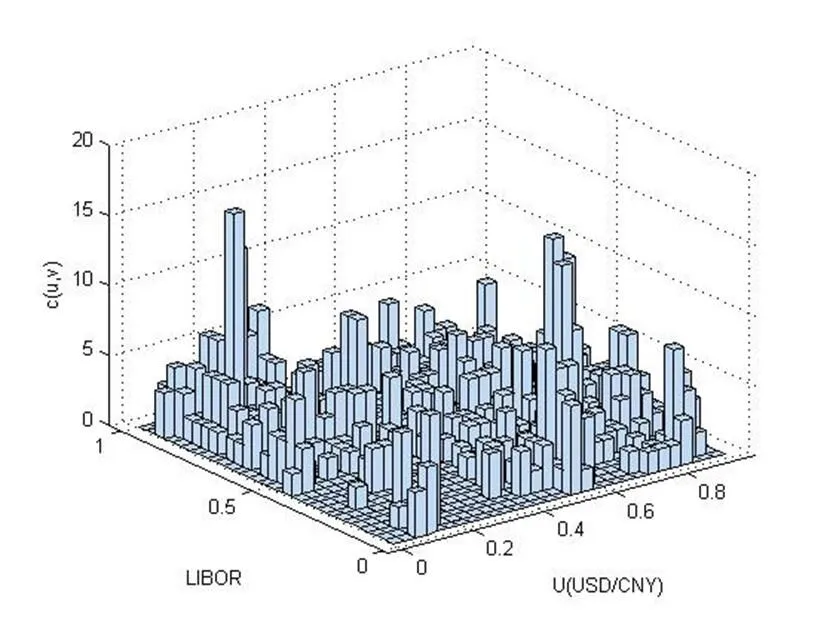
图9：USD/CNY和SHIBOR的联合频数直方图

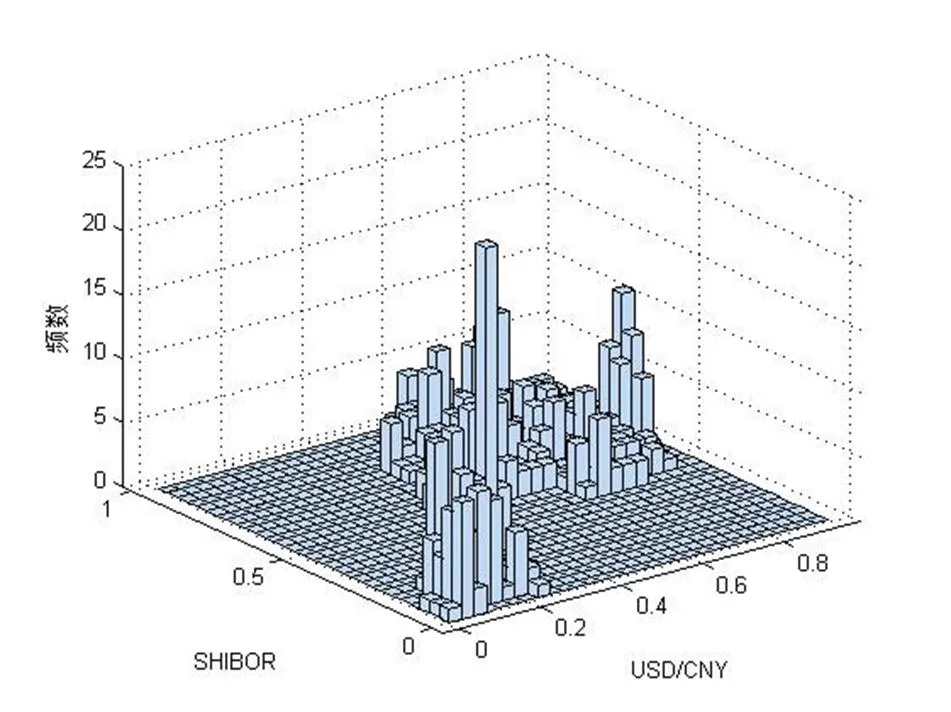
图10：USD/CNY和SHIBOR的联合频率分布直方图

由图8可以看出，USD/CNY和LIBOR之间尽管没有明显的对称性，但尾部具有较强的相关性，图10中两个变量的尾部亦表现出了相关性，因此可以选用对随机变量之间的尾部变化更为敏感的t-Copula函数来对USD/CNY、LIBOR和USD/CNY、SHIBOR的原始数据进行相关性拟合。

（2）USD/CNY与LIBOR的Copula函数参数估计

对于选取的t-Copula函数，先根据上文中的核分布估计求出USD/CNY、LIBOR的边缘分布，再调用Copulafit函数估计t-Copula函数的参数。根据MATLAB程序的显示结果，t-Copula函数的线性相关参数和自由度的估计值分别是：

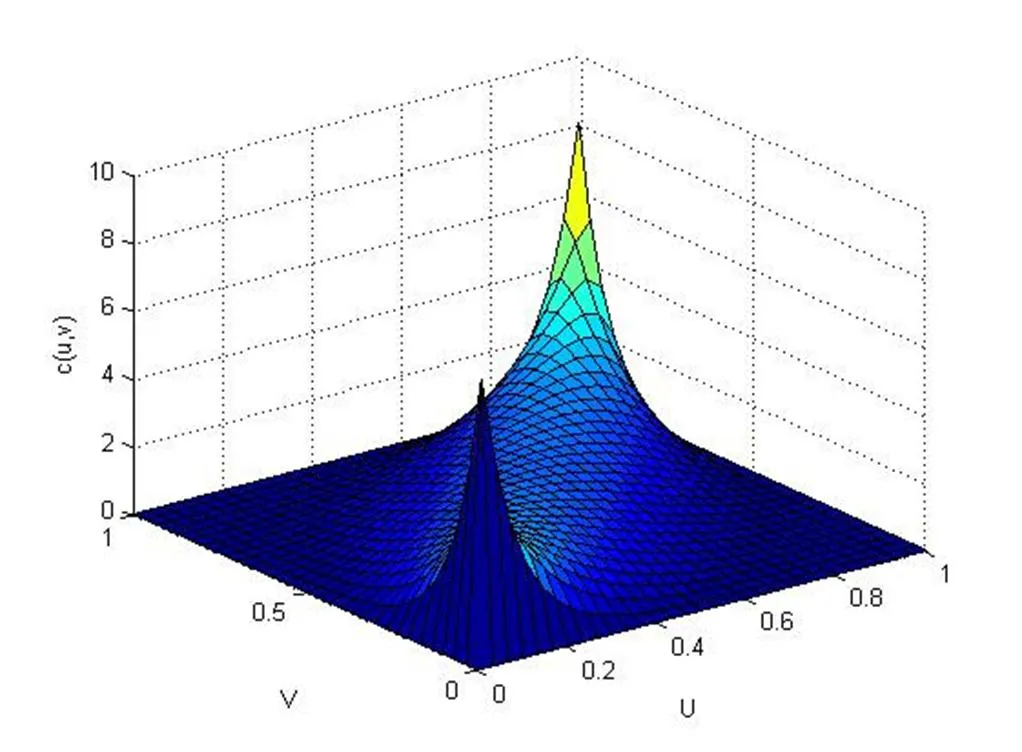
估计出t-Copula函数中的参数之后，再分别调用Copulacdf函数和Copulapdf函数计算t-Copula函数的分布函数值和密度函数，并绘制分布函数图和密度函数图。由图11可以看出，t-Copula函数具有很厚的尾部，图12可以看出USD/CNY、LIBOR之间具有较强的尾部相关性。

图11：C1（u，v）的分布函数图（ρ=-0.3850， k=5.68）

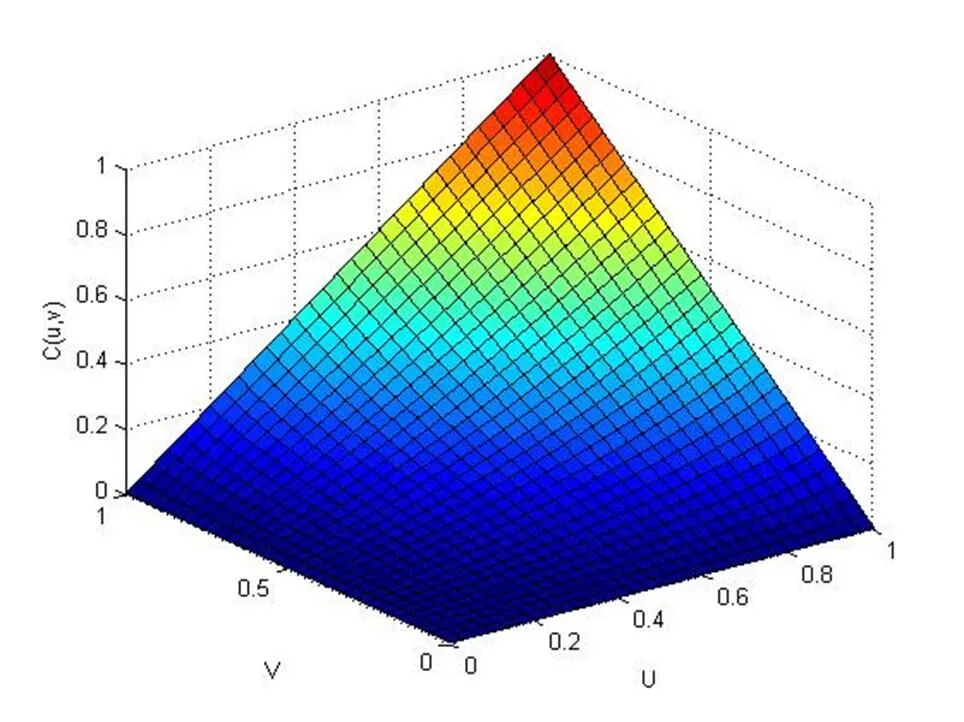
图12：C1（u，v）的函数密度图（ρ=-0.3850， k=5.68）

（3）USD/CNY 与 SHIBOR 的Copula 函数参数估计

用同样的方法来估计USD/CNY与SHIBOR的Copula函数的参数，t-Copula函数的线性相关参数和自由度k的估计值分别是

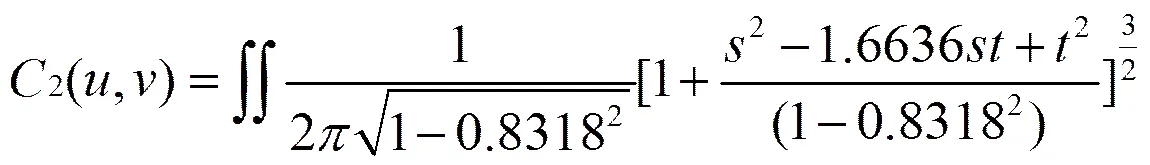
C2（u，v）的分布函数图和函数密度图分别由图13、图14所示：

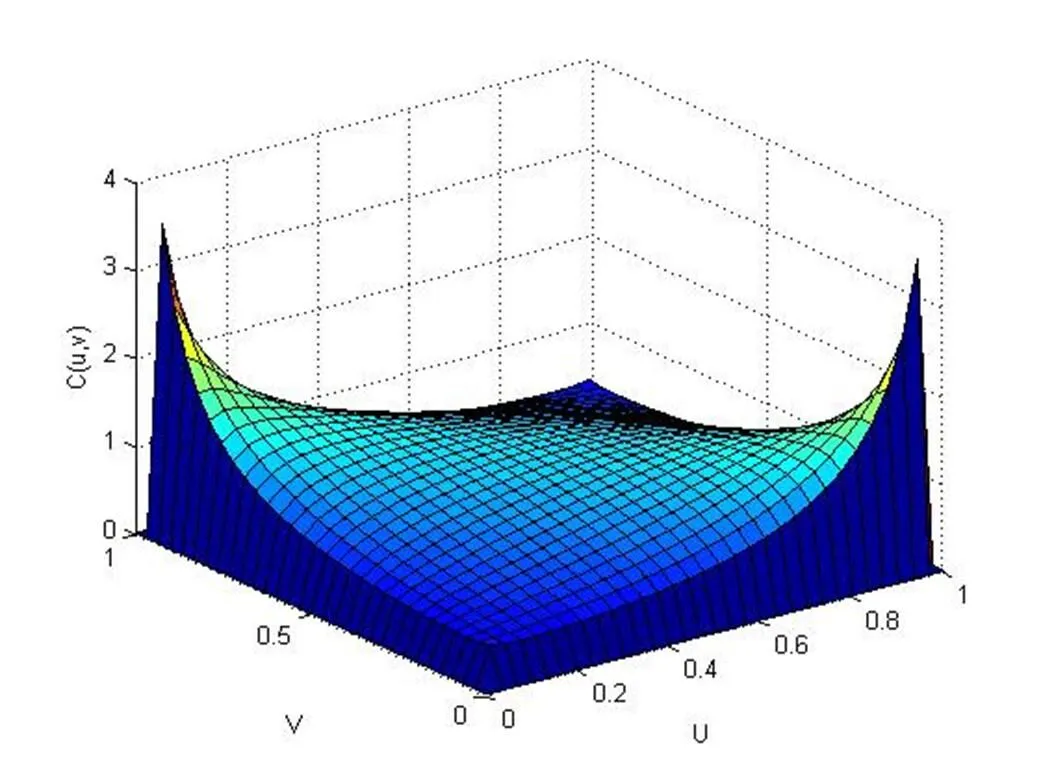
图13：C2（u，v）的分布函数图（ρ=0.8318， k=1.26）

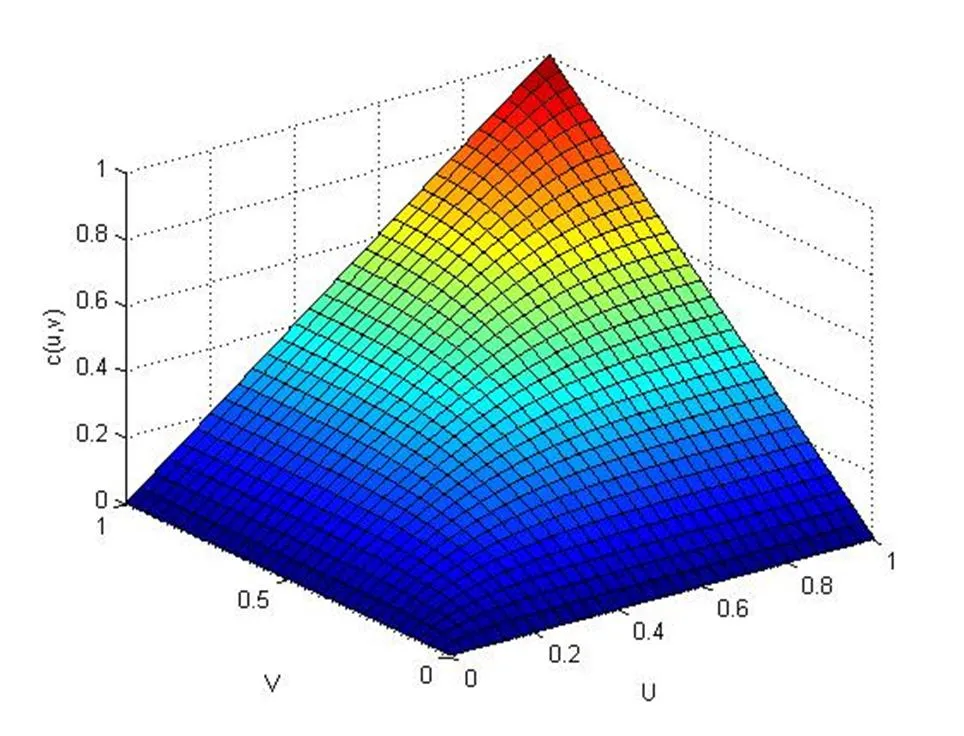
图14：C2（u，v）的函数密度图（ρ=0.8318， k=1.26）

4.汇率与利率的相关性检验

（1）USD/CNY与LIBOR的相关性检验

利用MATLAB软件，调用corr函数分析USD/CNY、LIBOR两组原始时间序列的相关性。

因为Kendall<0，Spearman<0，所以USD/CNY序列与LIBOR序列之间呈负相关，即国内市场的美元贬值，但美元利率确在上升。

（2）USD/CNY与SHIBOR的相关性检验

因为Kendall>0，Spearman>0，所以USD/CNY序列与LIBOR序列之间呈正相关，即国内市场的美元升值，人民币利率也会上升。

由于USD/CNY、SHIBOR的秩相关序数比USD/CNY、LIBOR的秩相关系数的绝对值更接近于1，所以美元对人民币汇率与人民币利率之间的相关性要强于美元对人民币汇率与美元利率之间的相关性。

（二）基于Copula函数的交易对手信用风险暴露计量

1.基于Copula函数的蒙特卡洛模拟数据的构建

上文通过t-Copula函数分析了美元对人民币汇率、美元利率、人民币利率之间的相关性，得出了美元对人民币汇率与美元利率之间存在负相关，美元对人民币汇率与人民币利率之间存在正相关的结论。此节将在相关性结论的基础上[21]，通过蒙特卡洛模拟生成一系列符合相关性结论的三组正态随机数（1000个/组），作为对未来美元对人民币汇率、美元利率、人民币利率走势的预期，并再次对资产组合的预期风险暴露值进行计算，验证汇率、利率之间的相关性对金融市场上金融衍生品资产组合的影响[22]。具体的模拟过程如下：

将C（）利用MATLAB软件生成两组随机数X、Y，此时X、Y之间的相关性与美元对人民币利率、美元利率之间的相关性一致，X、Y负相关。

C（）式中用X作为已知数生成另一随机数Z，此时X、Z之间的相关性与美元对人民币利率、人民币利率之间的相关性一致，X、Z正相关。

这样生成的Y组随机数与Z组随机数相互独立，并无直接相关性。

2.基于Copula函数数据的信用风险暴露计量

仍以表1和表2的资产组合作为计量现期信用风险暴露值的衍生品资产组合，由于X、Y，X、Z之间具有很强的相关性，因此带入现期风险暴露法中计算的风险暴露值会与原始数据的计算结果有着较大的差异。计算结果见表5。

表5：蒙特卡洛模拟下的交易对手现期信用风险暴露值

蒙特卡洛模拟下的资产组合的风险暴露值为920142元，大于基于原始数据计算出的风险暴露值749670元。因此，美元对人民币汇率、美元利率、人民币利率之间的相关性会对金融衍生品资产组合的稳定性产生影响，增加了资产组合的风险暴露。

（三）Copula函数的扩展应用

基于两次风险暴露值的比较可以看出，市场风险之间的相关性不仅能对交易对手信用风险暴露产生影响，还会因为风险的延续性而对资产组合的风险暴露产生更大的影响。由于短期内风险会继续上扬，因此金融机构在防范交易对手信用风险时，不仅要防范多种市场风险关联性所带来的风险，更要构建和调整资产组合以达到规避和对冲风险的目的。根据上文分析，Copula函数能够较好地拟合市场风险之间的相关性，并预测未来风险因素的变化，因此在实际中，当估算出Copula函数的参数后，可以利用相应的Copula函数、利率模型、汇率模型预估未来金融市场上汇率和利率的变化趋势，及时的调整资产组合或者构建新的对冲组合来降低风险。预计美元对人民币汇率上涨时，人民币利率也可能受影响而上涨，美元利率可能会下跌，则买入人民币利率产品或买入美元利率看跌期权；预计美元对人民币汇率下跌时，人民币利率预计会下跌，美元利率可能反而上涨，则应该更大比例地买入美元利率产品或减少持有人民币利率产品。

五、交易对手信用风险管理建议

信用风险的管理是一个较为复杂的过程，随着资产组合的复杂化发展，如何将信用风险控制在可控范围内，对于维护整个金融市场的稳定有着重要意义。根据本文对影响交易对手信用风险的相关因素的分析，现提出相关建议：

（一）构建衍生品资产组合

相对于投资单一的金融衍生品，构建衍生品资产组合能够更好的规避风险[23]。尽管在达成交易合约之前，交易双方都会评估对手方的违约概率来预先规避交易对手信用风险，但由于市场风险很不确定，所以即使在合约签订之后仍有可能出现未预料的违约。因此构建交易方向相反、能够产生对冲效应的资产组合能够有效地规避市场风险。金融机构在某一份合约中可能会出现亏损[24]，但是在其对冲合约中会出现盈利，最终的总风险暴露值会降低。

（二）加强对市场风险相关性的防范

基于本文三、四部分的分析，汇率与利率之间的相关性会对资产组合的风险暴露产生影响，这说明即使金融机构只参与了规避某一种市场风险的金融衍生品交易，例如购买了美元对人民币汇率掉期，但是当出现另外一种市场风险时，例如人民币利率发生变化，金融机构仍需要对汇率互换产品时刻进行风险评估，尽量控制风险暴露。因为人民币利率的变化会对美元对人民币汇率产生影响，所以最终利率市场的变化也会使汇率市场出现相应变化，进而影响衍生品资产的价值。另外，要根据Copula函数拟合金融市场的能力，合理地对未来市场的风险趋势进行预测，及时地调整资产规模或者构建新的资产组合，来达到规避和对冲市场风险的目的。

（三）采取风险缓释措施缓解风险

风险暴露虽然不能完全避免，但可以采取措施来降低风险[25]。在选定金融衍生品资产组合时，只能计算出当前的风险暴露，合约确定后，将来的风险暴露或资产组合的价值会根据未来市场的变化而波动，所以我们无法完全避免市场风险的影响，但是可以根据市场变化每日对所持头寸的价值进行估值，进而利用抵押品、保证金、净扣协议等风险缓释措施来缓解风险。如果机构自身的资产规模不足以承担违约风险，那就尽量选择占用资金较少的资产组合来进行风险规避。还要根据《巴塞尔协议Ⅲ》中提出的信用价值调整（CVA）标准[26]，在强化对CVA管理的同时，建立统一的CVA交易平台来有效规避错向风险。

（四）使用净额结算而非全额结算

净额结算是指交易对手存在多笔交易时，对这多笔业务进行汇总后再轧差结算。全额结算是指对每一笔业务都进行结算。因此使用净额结算能够避免在金融危机发生时，交易对手违约概率迅速上升的情况下风险暴露的急剧增加，可以使整个资产组合或者金融市场的风险暴露值较稳定，降低错向风险。

（五）引入中央交易对手

中央交易对手是为金融衍生品交易双方提供清算服务的中间人[27]，作为每一份交易合约买卖双方的对手方出现。中央交易对手作为独立的第三方机构，由其承担履约责任，就能最大程度的保证买方和卖方的权益。即使一方对中央交易对手违约，只要另一方守约，中央交易对手仍要履约，这就能有效地阻止交易对手信用风险的扩散程度。目前，中央交易对手也是最适合进行多边净额结算的中介清算机构。

[注 释]

① 参看GIBSON M S“Measuring Counterparty Credit Exposure to a Margined Counterparty”一文，载于2005年“FEDs Working Paper”，No. 2005-50。

② 参看PATTON MQ著《Qualitative Research and Evaluation Methods》一书，2002年第二版.第467页。

③ 参看ROCKINGER M和JONDEAU E “Conditional Dependency of Financial Series:An Application of Copulas”一文，载于Banque de France2001年的“Working papers”。

④ 数据来源：中国银行远期人民币外汇牌价

⑤ 数据来源：中国货币网

⑥ 数据来源：中国外汇交易中心www.chinamoneychinamoney.com

[参考文献]

[1] 符文佳.论银行业衍生产品交易对手信用风险管理[J].南京社会科学,2011(3):150-156.

[2] 王丽佳.第三版《巴塞尔协议》下我国商业银行信用风险管理研究[D].长春:东北师范大学,2013:5.

[3] 蒋昇.交易对手信用风险研究-基于Copula函数的实证分析[D].北京:中国社会科学院,2013:5.

[4] 杨华,卓骏.信用风险评估模型及其评述[J].经济论坛,2004(19):142-143.

[5] LOMIBAO D,ZHU S.A Conditional Valuation Approach for Path-dependent Instruments[J].Journal of Credit Risk,2005(8):1-18.

[6] MICHARL PYKHTIN,STEVEN H ZHU.A Guide to Modeling Counterparty Credit Risk[J].GARP Risk Review,2007(7/8):16-22.

[7] MICHAEL PYKHTIN,DAN ROSEN.Pricing Counterparty Risk at the Trade Level and Credit Valuation Adjustment Allocations[J].Journal of Credit Risk,2010(4):3-38.

[8] 章彰. “巴塞尔协议III”的交易对手风险管理改革及其借鉴[J].银行家,2011(3):63-65.

[9] 徐妙志.Copula理论及其在金融市场相依性分析中的应用[D].成都:电子科技大学,2013:5.

[10] PAUL EMBRECHTS,ALEXANDER MCNEIL,DANIEL STRAUMANN.Correlation and Dependency in Risk Management: Properties and Pitfalls[M].Cambridge:Cambridge University Press,1999:227-250.

[11] PERRAUDIN W R M,HU Y T,KIESEL RUDIGER.The Estimation of Transition Matrices for Sovereign Credit Ratings[J].Journal of Banking and Finance,2002(26):1-35.

[12] 张尧庭.连接函数(copula)技术与金融风险分析[J].统计研究,2002(4):48-51.

[13] 侯成琪,王频.基于连接函数的整合风险度量[J].统计研究,2008(11):72-80.

[14] 陈希镇,胡兆红.Copula函数的非参数核密度估计方法[J].统计与决策,2010(14):27-28.

[15] 任仙玲.基于Copula理论的金融市场相依结构研究[D].天津：天津大学,2008:8.

[16] 郝青霞.利率模型和利率衍生品的交易对手信用风险管理[D].济南：山东大学,2012:5.

[17] 任正亮.基于SHIBOR的人民币利率互换公允价值的估量[J].财会月刊,2008(6):53-54.

[18] 张永冀,张瑞君. A公司基于交易对手的信用风险管理[J].财务与会计,2013(03):32-33.

[19] 李堪,陈健.交易对手信用风险管理探析[J].商业银行,2013(3):62-64.

[20] 谢中华. MATLAB统计分析与应用40个案例分析[M].北京:北京航空航天大学出版社,2010:196-213.

[21] 翁泽南.蒙特卡罗方法在三类金融衍生产品定价中的应用[D].上海:上海师范大学,2013:4.

[22] 陈翊,贾瑛瑛.交易对手信用风险管理[J].中国金融,2012(8):30-32.

[23] 中国人民银行合肥中心支行金融稳定处课题组.交易对手信用风险管理改革及启示[J].金融发展评论,2012(1):63-67.

[24] 罗猛.交易对手信用风险管理[J].中国金融,2012(4):30-32.

[25] 陈旭鸣.现在信用风险管理模式发展研究[J].统计与决策,2008(9):186-188.

[26] 冯启德.新巴塞尔协议视角的商业银行信用风险管理研究[D].上海:复旦大学,2006:10.

[27] 高成兴,符文佳.论中央交易对手与交易对手信用风险管理[J].中南财经政法大学学报,2010(5):74-79.

An empirical analysis on the management of counter party’s credit risk

YU PING, YU XUEJIAO

Credit default events due to the participation of OTC derivatives have caused a big impact on the entire financial system in recent years. Therefore, it is particularly important to prevent counter party’s credit risk. Based on constructed financial derivatives portfolio, this paper discusses correlation between exchange rate and interest rate according to t-Copula function fitting result, and then researches the effects of changes in market risk on counter party credit exposures according to losses and gains of portfolio. Finally, some measures are suggested to prevent financial risk correlation including converting settlements, focusing on risk mitigation measures, introducing transaction counter parties,etc.

Counter party’s credit risk; Copula function; Risk exposure

F83

A

1008-472X(2016)05-0033-10

2016-04-16

中国-东盟研究院“教育部长江学者和创新团队发展计划”资助 (CWZ 201416)

喻 平（1972-），男，湖北公安人，武汉理工大学经济学院教授，研究方向：金融发展与金融创新、金融风险管理；

于雪皎（1992-），女，山东威海人，武汉理工大学经济学院应用经济学硕士研究生、英国杜伦大学金融学硕士研究生，研究方向：金融风险管理。

本文推荐专家：

王仁祥，武汉理工大学，教授，研究方向：金融创新与金融工程、金融风险管理。

李志生，中南财经政法大学，教授，研究方向：市场微观结构、多风险暴露下的消费与投资决策。