基于Stewart平台的商用车保险杠疲劳仿真研究

闫鑫　姜迪　徐中皓　李鼎

（中国第一汽车股份有限公司技术中心，长春　130025）

基于Stewart平台的商用车保险杠疲劳仿真研究

闫鑫姜迪徐中皓李鼎

（中国第一汽车股份有限公司技术中心，长春130025）

基于Stewart平台原理建立了商用车保险杠总成疲劳仿真系统平台。以某试车场的道路载荷谱为目标信号进行了虚拟载荷迭代，获得了保险杠总成在实际耐久路面的疲劳载荷，进而对其进行了疲劳寿命预测。通过对比测量点的应变信号，在时域、频域及雨流域上达到较好对比结果，表明基于Stewart平台的疲劳仿真方法具有较高的精度，能够为包括保险杠在内的商用车零部件系统进行疲劳寿命预测，在控制其耐久性能的同时大幅节约研发时间。

主题词：商用车保险杠疲劳寿命预测虚拟载荷迭代

1　前言

商用车保险杠系统在满足安全防护功能的同时还需要满足自身结构的疲劳耐久要求，因此汽车企业在投产前要对汽车保险杠总成进行强化路耐久测试。国内外学者对于保险杠的研究多集中于碰撞性能仿真，以及基于碰撞性能的结构优化分析和轻量化研究等方面，鲜有研究其结构疲劳强度方面的相关文献。虽然某汽车研发单位利用电磁振动台对保险杠总成进行扫频试验获得了共振频率，并对其进行共振疲劳测试以考察结构的疲劳耐久性能，但这种方法容易使保险杠总成结构强度设计过剩，而且单自由度振动无法涵盖保险杠在随机路面振动时的多自由度激励耦合现象，对单自由度电磁振动台的仿真分析亦存在这样的问题，所以如何针对保险杠总成进行路面振动复现及其有限寿命设计，是进行疲劳仿真分析的关键。

Stewart平台是一种包含6个驱动分链的并行机构，具有工作空间小、刚性好及运动精度高等优点，被广泛应用于模拟承载件在自然条件下的多自由度运动状态。为此，本文利用Stewart平台特性，针对某重型商用载货车保险杠总成进行动力学仿真及结构疲劳性能分析。

2　疲劳载荷的获取

对保险杠结构疲劳分析的关键是获取其疲劳载荷。由于实际道路试验无法测得其疲劳载荷，因此需要利用可测得的保险杠总成数据（如加速度信号）作为目标信号，通过系统多体动力学模型作为传递函数，利用Stewart平台逆向运动变换定义清晰唯一的优点［5］反求施加在系统中的驱动量，同时由于系统的非线性因素影响，还需要通过不断迭代使系统响应信号无限趋近于目标信号，达到使Stewart平台位姿逆解的目的，即对保险杠总成进行路面振动复现。依此获得的驱动信号即可使系统的运动学与动力学状态与实际一致，提取出的疲劳载荷可作为后续疲劳分析的准确输入。

2.1Stewart平台介绍

如图1所示，Stewart平台的6个驱动分链的一端被成对安装在机械基板（静平台）上，而另一端交叉连接并安装在活动平台上，活动平台上的承载件能够以6个自由度进行运动，包含3个线性移动自由度（垂向、侧向和纵向）和3个旋转自由度（俯仰、横摆及侧倾）的运动能力。Stewart平台中静平台与地面固定连接，6个作动缸壳体与地面之间为球铰，6个作动缸活塞与活动平台为万向节连接，6个作动缸壳体与作动缸活塞为圆柱副连接。

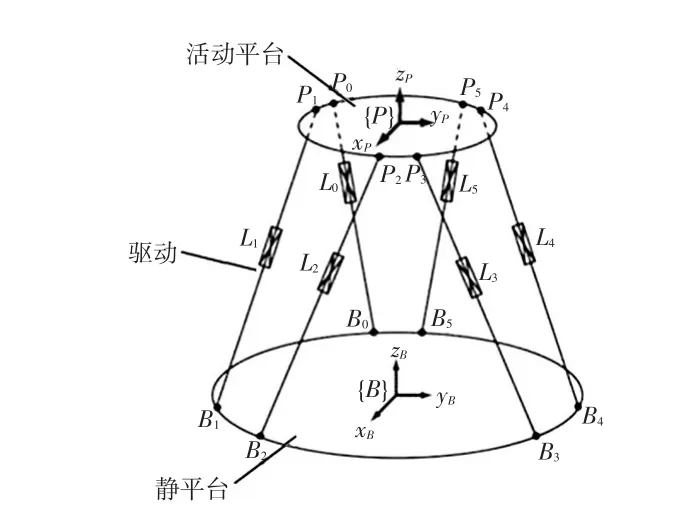
图1　Stewart平台

2.2多体动力学模型建立

多体动力学模型的实质是作为虚拟迭代中的传递函数，直接反映了系统的动力学响应特性。基于Stewart平台的商用车保险杠多体动力学建模是一个系统工程，需要确定系统硬点位置、部件连接关系、刚体质量质心和转动惯量以及非线性元件动态特性等一系列参数，同时还要考虑实际配重、保险杠柔性化处理、驱动位置及传感器布置位置等问题。

承载件部分主要由固定夹具、前横梁及保险杠总成本体构成，固定夹具分别与Stewart平台的活动平台和前横梁进行固定约束，前横梁与保险杠本体固定约束。为获得准确的系统动力学模型，保证传递函数的精度，需将保险杠本体进行柔性化处理。首先将保险杠进行网格划分，对不同零件分别赋予材料及属性，然后利用Nastran Craig-Bampton求解方式计算其模态频率，提取其在关注频率范围内的固有频率值并设置合适的结构模态阻尼参数，最后通过对比模态试验结果保证其结果精度。需要注意的是，大灯及雾灯机构作为集中质量存在，并不对其做详细建模。系统动力学模型如图2所示。

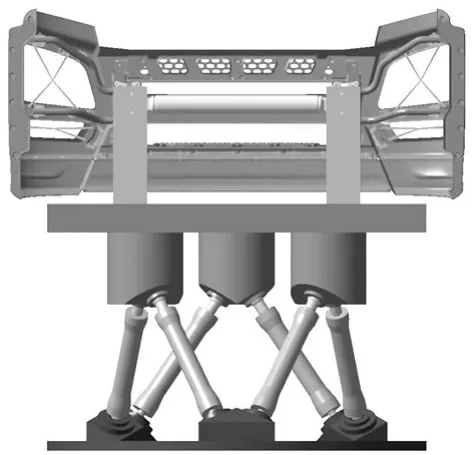
图2　系统多体动力学模型

2.3道路信号采集

为获得保险杠的实际路面响应进行了道路信号采集，信号采集所用传感器为加速度传感器与应变片。加速度传感器均为XYZ三向传感器，为满足保险杠本体的动力学响应，同时减少高频扰动影响，传感器被布置在保险杠支撑管内侧与外侧，如图3圆圈处。其中的部分加速度传感器信号作为虚拟迭代的目标信号，而另外一些信号作为监测信号以验证多体动力学模型精度。应变片的类型为单片，布置在应力集中敏感区域，如支撑管折弯处，见图3矩形标示处。应变片的测量信号用作验证疲劳分析结果的精度。

图3　传感器布置位置

在某试车场的耐久强化环路上对该商用车进行了路谱采集，测量时的车速在企业标准要求范围内。为保证信号的稳定性，测量了3个循环试验的信号，以保证至少两个循环试验的信号具有较好的一致性。测量的典型路段包括卵石路、鱼鳞坑、扭曲路、石板路等。

在所获得的原始信号中选取3个循环试验中较为稳定完整的一个周期信号作为首选数据，检查信号的合理性，然后对信号进行偏移修正、毛刺删除、漂移消除等前处理，结果如图4所示，最后将信号进行典型路段划分，以便于后续的虚拟迭代工作。

2.4虚拟载荷迭代

因保险杠本体固定点处的疲劳载荷需要用虚拟仿真的方法获得，为此采用了虚拟试验台的方法来获取疲劳载荷。虚拟试验台方法也叫半解析法，需要测量结构的加速度信号或相对位移信号作为目标响应信号。虚拟试验台可以避开轮胎模型精度和路面轮廓采集试验复杂性的影响，通过结合样车道路试验的准确性和多体模型仿真的高效性，利用疲劳等效原理反求施加在Stewart活动平台上的位移激励来模拟保险杠真实运动，这一过程被称作虚拟载荷迭代。

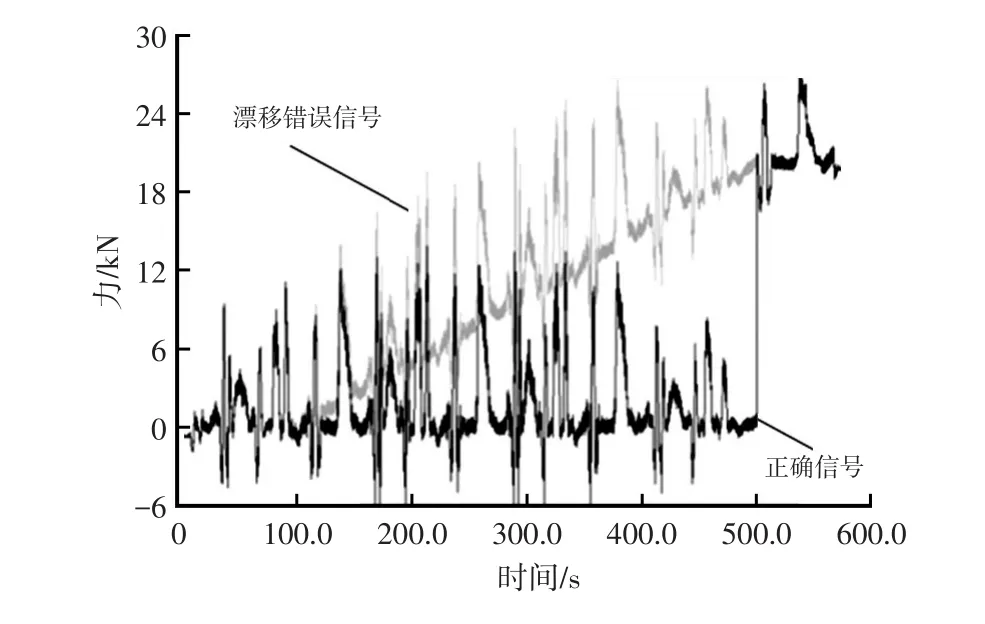
图4　信号前处理结果

迭代的一般过程为：生成白粉红噪声（WPN）unoise，将白粉红噪声输入多体动力学模型求得响应ynoise，并计算传递函数F=ynoise/unoise；将路试得到的加速度信号ydesired作为目标信号，通过FRF逆函数求出第1次驱动u0=F-1ydesired；反复迭代，un+1=un+F-1（）ydesired-yn，并比较第n次迭代的响应信号yn与目标信号ydesired的误差均方根值（RMS），以使其无限趋近于0，保证通道的收敛特性，同时确保时域频域信号的幅值与相位吻合度较高，停止迭代，以最后一步迭代获得的位移模型来提取结构接口点疲劳载荷。迭代过程如图5所示。

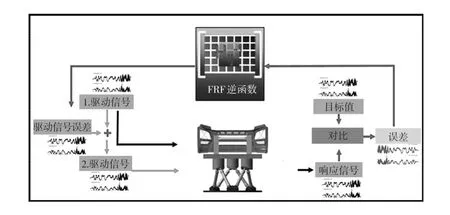
图5　虚拟载荷迭代过程

Stewart平台有6个驱动输入通道，为获得较好的传递函数，目标响应输出通道也应不少于6个。通过试验研究，并结合保险杠实际振动方向发现，保险杠迭代目标点应选取对称布置的至少4点，选点方式不唯一，因为理论上来说只要结构模态阻尼比率设置合适即能达到同样的迭代效果且位姿逆解值唯一。根据这一原则，在进行虚拟载荷迭代时，在保险杠外侧上、下共设置4个三向传感器测量点（A2、A3、A5、A6）为目标信号点（共12个通道），设置两个为监测信号点（A1和 A4，共6个通道），如图6所示。

图6　迭代目标传感器设置

按照迭代流程进行虚拟迭代并对其结果精度进行检测。图7为目标信号A3点Z通道迭代结果，由图7可看出，目标信号与响应信号无论在时域还是频域范围内均达到了比较高的吻合度。图8为监测信号A1点Y通道迭代结果，监测信号与响应信号吻合程度也较为理想。参考表1，各通道信号无论是目标信号还是监测信号，其仿真与测试的误差百分比均在10%以下，充分说明在Stewart平台驱动输入下，保险杠总成的动力学响应特性与实际工况较为一致，依此获得的保险杠接口点疲劳载荷真实可信，可以作为疲劳分析的输入。

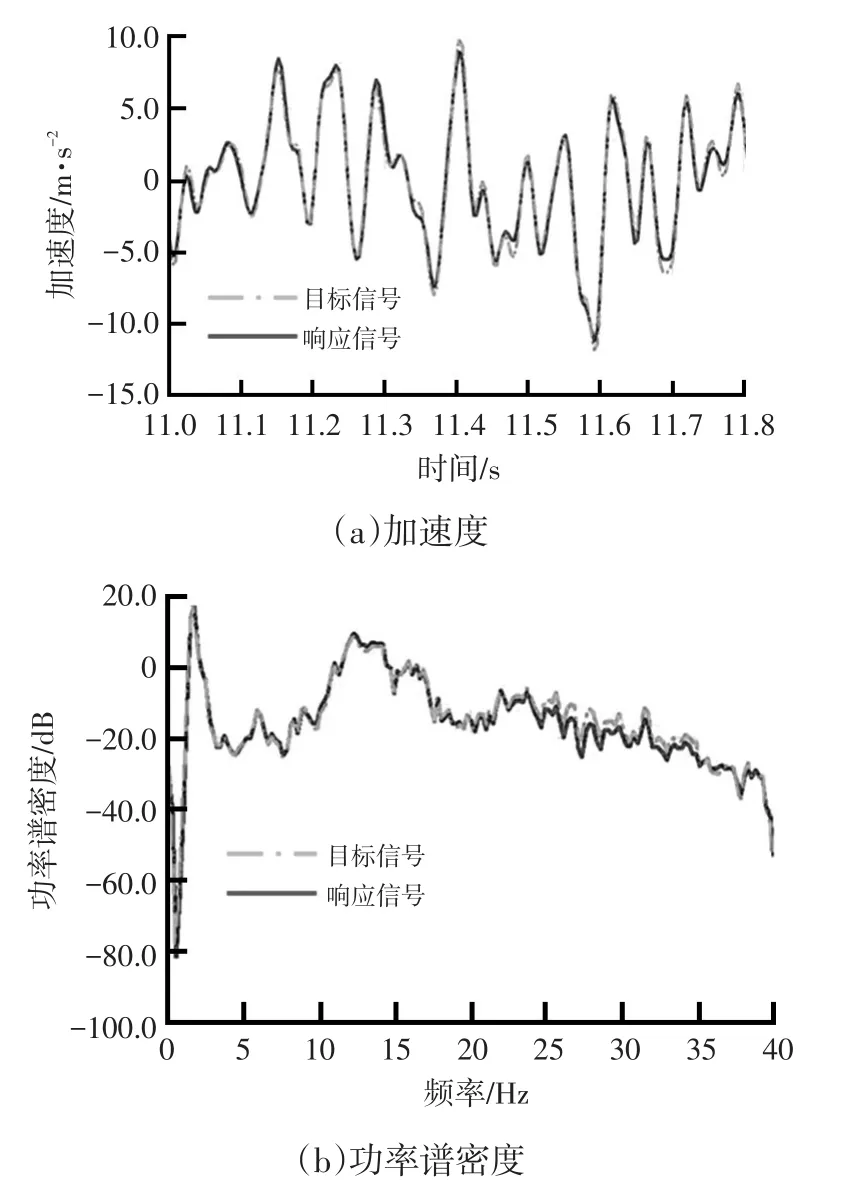
图7　目标信号A3点Z通道迭代结果

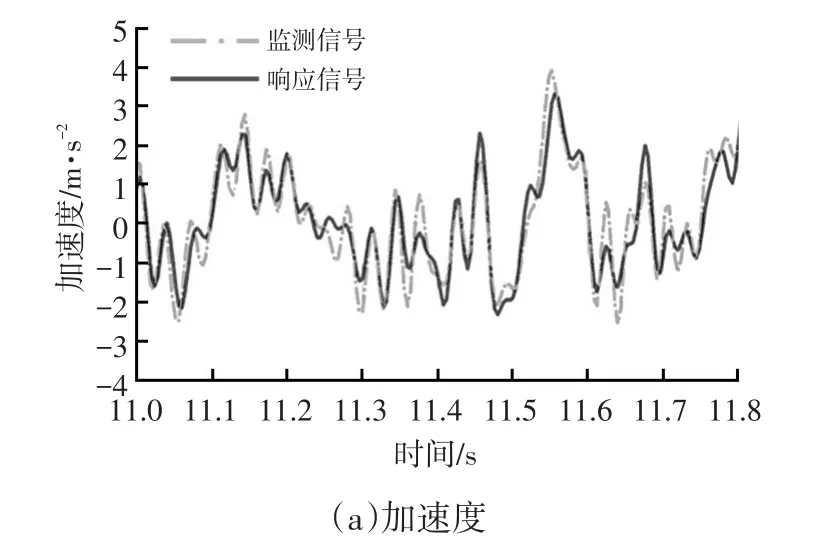
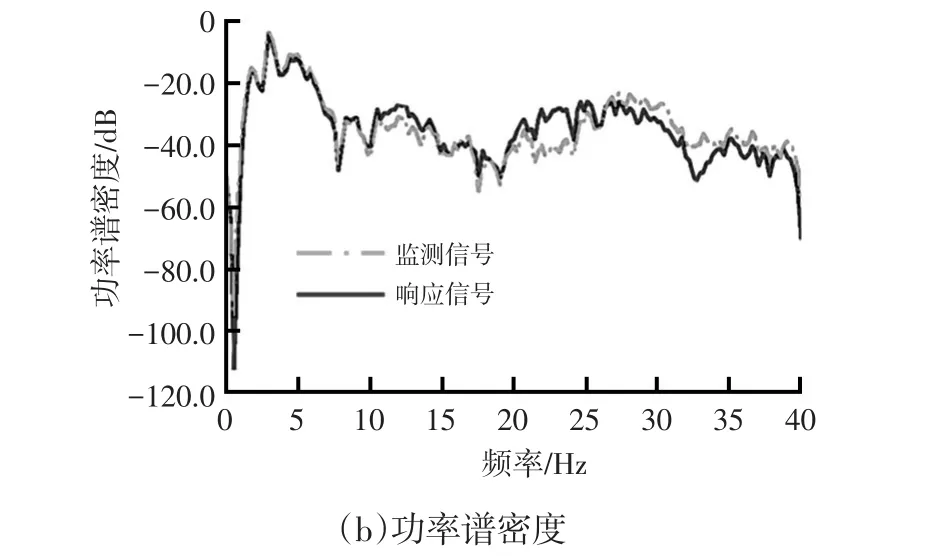
图8　监测信号A1点Y通道迭代结果

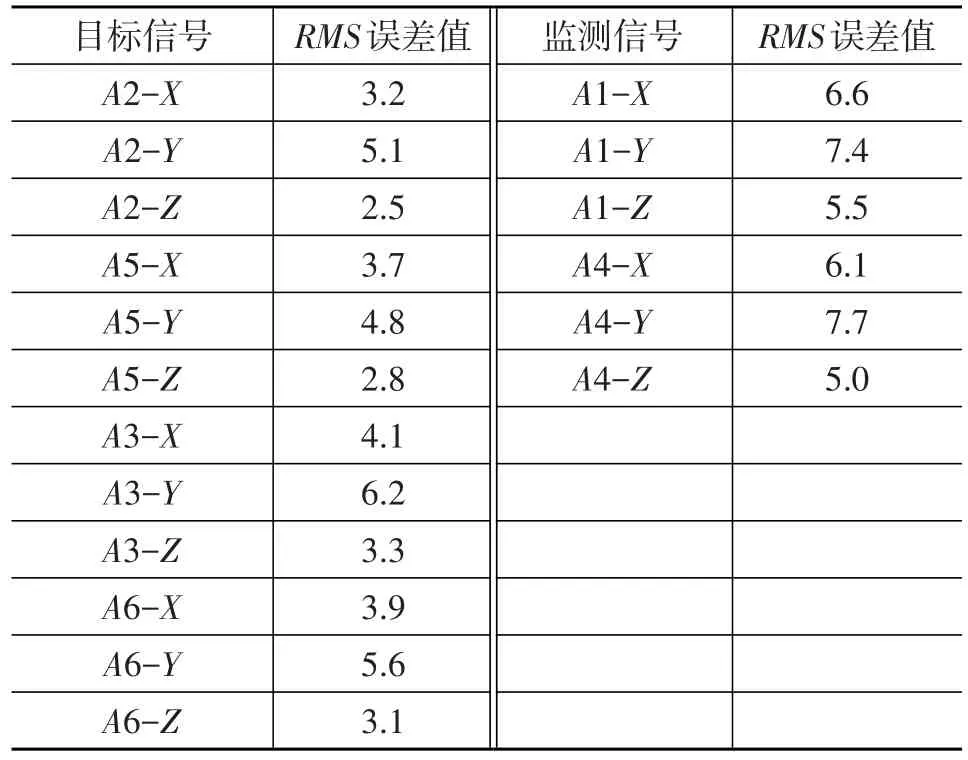
表1　各通道信号仿真与测试结果RMS（标准差）误差%

3　疲劳寿命分析与结果验证

由于保险杠总成的非金属结构件材料为各向异性，难以获得准确的输入，所以本研究主要针对其金属结构件进行疲劳寿命预测分析。在进行疲劳寿命分析时，首先要进行全内饰结构的有限元建模，其次进行惯性释放计算求出单位力作用下加载点的应力分布，然后将虚拟载荷迭代得到的疲劳载荷、惯性释放应力以及材料特性曲线同时输入到疲劳求解器中进行计算，最后再依据得到的疲劳损伤结果对其进行结构寿命预测。

针对结构件的缺口效应及局部塑性变形特性，采用应变寿命分析方法即ε-N法计算其疲劳损伤，表达式为：

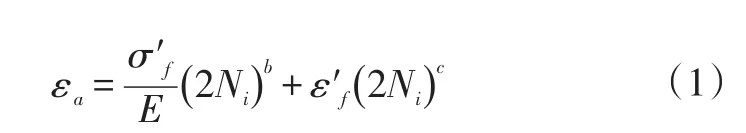
式中，εa为应变幅；σ′f为疲劳强度系数；ε′f为疲劳韧度系数；b为疲劳强度指数；c为疲劳韧度指数；Ni为各种应变幅下的寿命。

由于应力循环的作用，金属材料会出现循环硬化和循环软化现象，则εa计算式变为：

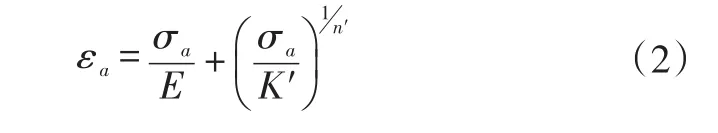
式中，E为弹性模量；σa为应力幅；K′为循环强度系数；n′为循环应变硬化指数。

根据式（1）与式（2），再根据Miner线性损伤累积法则及P-SWT修正方法［6］，即可计算获得保险杠结构的疲劳损伤值。经过疲劳计算获得的载荷单一循环疲劳损伤分布云图如图9所示，由图9可看出，试验用商用车保险杠疲劳危险点主要有2处，分布在保险杠下固定点局部区域结构拐角处，均属应力集中影响较大区域，损伤值分别为3×10-4和1×10-5。根据某试车场道路耐久性能要求，其结构寿命应大于8 000 km，由于环路单个循环为5 km，则应满足循环数为1 600，所以1个循环造成的损伤应为1/1 600，即6.25×10-4。该商用车保险杠疲劳危险点损伤值均小于6.25×10-4，表明保险杠疲劳寿命满足强度要求。

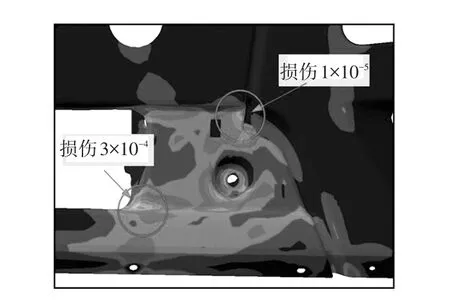
图9　结构疲劳危险点

根据应变疲劳方法基本原理，决定零部件疲劳强度和寿命的是应变集中处的最大局部应力应变，只要最大局部应力应变相同，疲劳寿命就相同［9］。所以为验证疲劳计算精度，将某路段下道路试验测量得到的试验用商用车保险杠支撑管应变片信号与疲劳仿真计算的应变信号进行对比，结果如图10所示。由图10可看出，仿真信号与试验信号达到较为理想的吻合程度，经统计仿真值与测试值的RMS误差百分比为7.8%（＜10%），表明疲劳计算结果精度较高。存在误差的原因是由于结构非线性以及实际应变测量点与仿真考察位置存在一定差距而导致的。

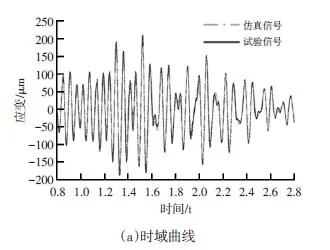
图10　应变信号的时域、频域、雨流域对比曲线

4　结束语

本文基于Stewart平台，对某重型商用载货车保险杠总成系统进行了疲劳仿真研究，从多体动力学建模、路谱采集、虚拟载荷迭代及疲劳寿命分析等方面进行了阐述。通过对比仿真与试验应变曲线发现，疲劳仿真结果精确度较高，表明基于Stewart的疲劳仿真方法可获得保险杠总成结构的疲劳耐久寿命，利用该方法可在新开发车型的设计前中期对部件进行疲劳寿命预测及结构优化改进，大幅缩短产品研发周期。

1赵强.Stewart平台的振动研究.机械科学与技术，2004，5 （23）：594～597.

2仇原鹰.基于IDEAS软件的Stewart平台机构建模与动力仿真.机械科学与技术，2005，8（24）：898～901.

3刘志星.联合仿真平台下飞行模拟器Stewart平台及其负载控制研究.机床与液压，2015，3（43）：72～81.

4Khalifa H.Harib.Axiomatic Design of Hexapod-based Machine Tool Structures.SAE，2008-01-0750.

5Takahiko Murano.Development of High-Performance Driving Simulator.SAE，2009-01-0450.

6Yung-Li Lee.疲劳试验测试分析理论与实践.北京：国防工业出版社，2011.

7王忠校.载货汽车驾驶室疲劳仿真方法研究.汽车技术，2014（7）：54～58.

8徐刚.基于虚拟振动台的疲劳寿命预测研究.同济大学学报，2009，37（1）：97～100.

9秦大同.疲劳强度与可靠性设计.北京：化学工业出版社，2013.

10Sawa N，Nimiya Y and Kubota Y.Fatigue Life Prediction on Rough Road Using Full Vehicle Co-simulation Model with Suspension Control.SAE，2010-01-0952.

（责任编辑文楫）

修改稿收到日期为2016年7月29日。

Fatigue Simulation Analysis of Commercial Vehicle’s Bumper System Based on Stewart Platform

Yan Xin，Jiang Di，Xu Zhonghao，Li Ding
（China FAW Co.，Ltd R&D Center，Changchun 130025）

Fatigue simulation system platform of commercial vehicle bumper assembly was built based on the theory of Stewart platform.Virtual load iteration was performed by adapting road load spectrum of proving ground as the target signal to obtain the fatigue load of bumper assembly on real durable road，thus to predict its fatigue life.By comparing strain signals of the key point，good comparative results were obtained in the time domain，frequency domain and rainflow domain，indicating that the fatigue simulation method based on Stewart platform had high precision.Therefore the commercial vehicle components including bumper system can be predicted for its fatigue life so as to control the durability performance and shorten development cycle significantly.

Commercial vehicle bumper,Fatigue life prediction,Virtual load iteration

U463.83

A

1000-3703（2016）09-0022-05