基于多分辨分析的MEARTH方法及其在汽车安全仿真模型确认中的应用

张玉峰　詹振飞　李君明

（重庆大学，重庆　400044）

基于多分辨分析的MEARTH方法及其在汽车安全仿真模型确认中的应用

张玉峰詹振飞李君明

（重庆大学，重庆400044）

针对仿真模型确认中存在的多元和动态响应问题，提出了一种基于多分辨分析的MEARTH方法，并设计了一种基于贝叶斯决策理论的分类器来综合考虑不同响应的模型确认结果，从而可对多元动态系统的仿真模型的有效性做出综合评估。通过对某汽车乘员约束系统进行模型确认表明，利用所提出方法得到的评分比传统MEARTH方法的评分更稳定，可对多元动态系统仿真模型的有效性做出合理评判。

主题词：多元动态系统多分辨分析汽车安全仿真模型确认

1　前言

基于仿真模型的设计常用于汽车产品开发，在产品开发前期必须对模型的有效性和预测能力做出定量评价，而模型确认就是为了评估仿真模型的有效性和预测能力而对其输出数据与试验数据进行对比的一个过程。近年来，开发定量的模型确认方法引起了不少学者的关注，如Sendur等［1］提出了AVASIM方法，使用L1范数的算法来评估仿真模型的有效性和准确性；Pope等［2］提出了基于互相关系数的R-平方方法，采用互相关系数来表征试验与仿真的响应；Geers［3］提出了一种综合了幅度和相位误差的时间序列对比方法，但没有考虑形状误差；Donnelly和Morgan等［4］提出了正归积分平方误差方法，同时考虑了相位、幅度和形状误差；Sarin、詹振飞等［5～10］提出了响应误差评估方法（Error Assessment of Response Time History，EARTH）及对其改进后的MEARTH（Multivariate Error Assessment of Response Time History，MEARTH）方法。然而上述模型确认方法没有对时间序列信号中的不同成分进行分析，只是对单个响应的仿真时间序列与试验时间序列的对比，不能直接对面向汽车安全的不确定性多元动态系统仿真模型进行验证。本文针对上述问题，首先基于Mallat算法对时间序列进行多分辨分析，将重构后的低频部分和高频部分进行MEARTH评分，按重要程度加权组合，并设计了一种基于贝叶斯决策理论的分类器来综合考虑不同响应模型的确认结果，从而对多元动态系统仿真模型的有效性做出合理的评判。

2　动态系统仿真模型的误差量化

本文提出的基于多分辨分析的MEARTH方法的流程如图1所示。其中，CAE数据和试验测量数据是不同时刻下不同响应的观测值。

图1　基于多分辨分析的MEARTH方法流程

由于多元动态系统不同响应的量纲不同，为了消除量纲对误差量化的影响，首先对仿真数据和试验数据进行归一化处理，化为无量纲量。因不同响应之间存在相关性，为了减少重复误差，对归一化后的数据进行主元分析，以达到降维的目的。从幅度误差、相位误差和形状误差3个方面来对降维后的数据进行误差量化，并对降维后的数据进行Mallat分解，对分解后的不同频率成分按重要程度给予相应的权值。然后对每个响应的3种误差进行评分（转化为无量纲评分），并根据专家经验确定3种误差的权值大小，进而得到各响应的评分，最后通过设计基于贝叶斯决策理论的分类器来综合考虑各响应的验证结果，从而对多元动态系统仿真模型的有效性做出合理评估。当模型能够有效反映实际的动态系统时，则该模型就可用于产品的开发。反之，则需要对仿真模型的参数进行调整优化。

2.1主元分析

令T=［t1，L，tm］T为n×m维的试验数据，其中为降维后的数据，维数为n×p（p≤m），，即降维后的主元。降维后的数据应至少保留原来数据95%的信息，可由协方差矩阵的特征值确定：

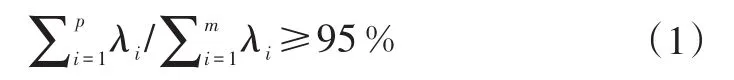
权重矩阵W的维数为m×p，由特征向量λ1…，λp组成。原数据与降维数据之间的关系可表示为：

式（2）描述了T与ΦT之间的关系，参数向量μT由T数组的m个均值组成，亦即μT=（1/N）。因此ΦT可表示为：

2.2多分辨分析

多分辨分析是小波理论中的重要部分，20世纪80年代末，Mallat在构造正交小波基时提出了多分辨分析的概念，并提出了正交小波构造和变换的快速算法，即Mallat算法。该算法将试验数据和仿真数据分解到不同分辨率的空间上，比较它们在不同空间上的吻合程度，并按重要程度进行加权组合。

2.3误差分析

因互相关系数与相位误差存在一定的关系，相位误差越小，互相关系数越大，所以采用互相关系数来处理和分析试验与模型仿真两个时间序列之间的相位误差，试验数据与模型仿真结果的互相关系数为：

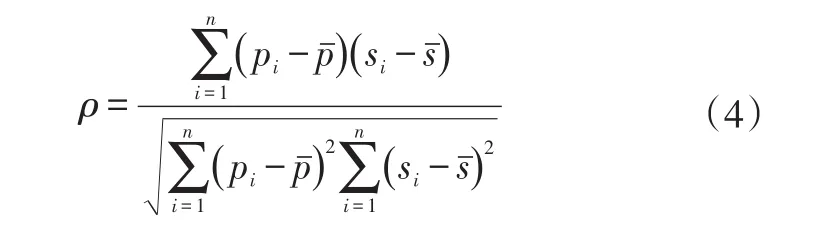
式中，pi、s（ii=1，2，3，…，n）分别为试验和仿真模型曲线上第i点数据；p¯、s¯分别为试验和模型仿真相应的数据均值；n为数据点数量。

移动时间序列，计算新的互相关系数，直到互相关系数达到最大，用此时移动的步数nph来表示相位误差eph。

为避免相位误差对计算幅度误差和形状误差的影响，采用时移序列代替原序列，时移后的试验和仿真的时间序列为Pts和Sts。因为试验数据和模型仿真数据的波峰、波谷很难严格对齐，给后续幅度误差和形状误差的计算带来很大干扰，因此利用动态时间规整技术（Dynamic Time Warping，DTW）对试验和模型仿真时间序列进行规整，规整后的试验和模型仿真时间序列为Pts+w和Sts+w。消除相位误差和规整后，幅度误差为：

采用斜率来量化形状误差，可以避免幅度误差对计算形状误差产生的影响，形状误差计算式为：

式中，Pts+d+w和Sts+d+w为经过时移和规整后的试验和模型仿真曲线斜率。

2.4误差评分

计算出某一响应的幅度误差、相位误差和形状误差后，为统一3种误差的量纲，可参考文献［4］和文献［5］中的误差评分方法得到3种误差的0～100%无量纲评分，其计算式为：

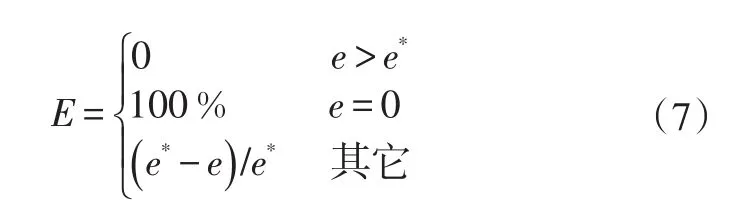
式中，E为误差评分；e*为可接受的误差上限；e为量化误差。

2.5计算总误差

得到响应的相位误差、幅度误差和形状误差评分后，需要根据3种误差的评分计算出总的误差评分。因为对仿真模型的相位误差、幅度误差和形状误差要求不同，需要根据专家经验确定3种误差的权值（ωph、ωma和ωsh）大小，然后计算总误差评分，计算式为：E=ωphEps+ωmaEma+ωshEsh（8）式中，Eph、Ema、Esh分别为3种误差的评分。

3　分类器设计

分类是数据挖掘的一种非常重要的方法，分类的概念是指在已有数据的基础上确定一个分类函数或构造出一个分类模型（即分类器Classifier）。分类器是数据挖掘中对样本进行分类的方法的统称，分类的方法众多，其中贝叶斯分类器是根据待分类数据后验概率的大小进行分类的，后验概率［6］计算式为：

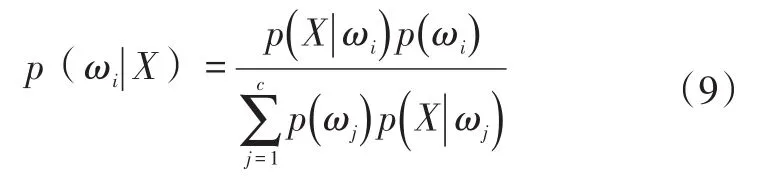
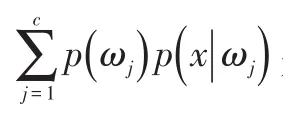
经最终化简后的判别函数为：

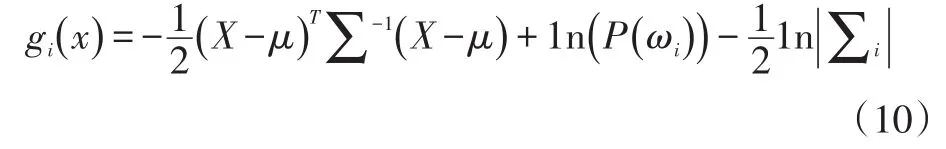
式（10）中，均值向量μi和协方差矩阵∑是未知的，可根据对仿真模型的要求生成训练数据对分类器进行训练来确定μi和∑的值。

4　案例分析

为验证本文所提出方法的可行性，利用该方法对某汽车乘员约束系统进行模型确认，并与传统的MEARTH方法得到的结果进行了对比。该乘员约束系统模型包含9个响应，每个响应的试验数据和模型仿真数据都是由203个点组成的时间序列。通过改变试验条件，共得到6组试验数据和模型数据。

选取其中1组数据进行分析，首先对该组数据的9个响应进行归一化处理，然后对处理后的数据进行主元分析，结果如图2所示。因前3个主元的贡献率达到95.18%，所以可以将原来的9维数据减少到3维，3个主元的试验和仿真曲线如图3所示。

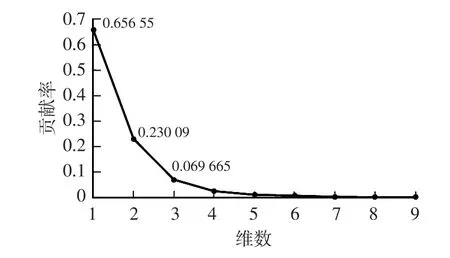
图2　主元分析结果

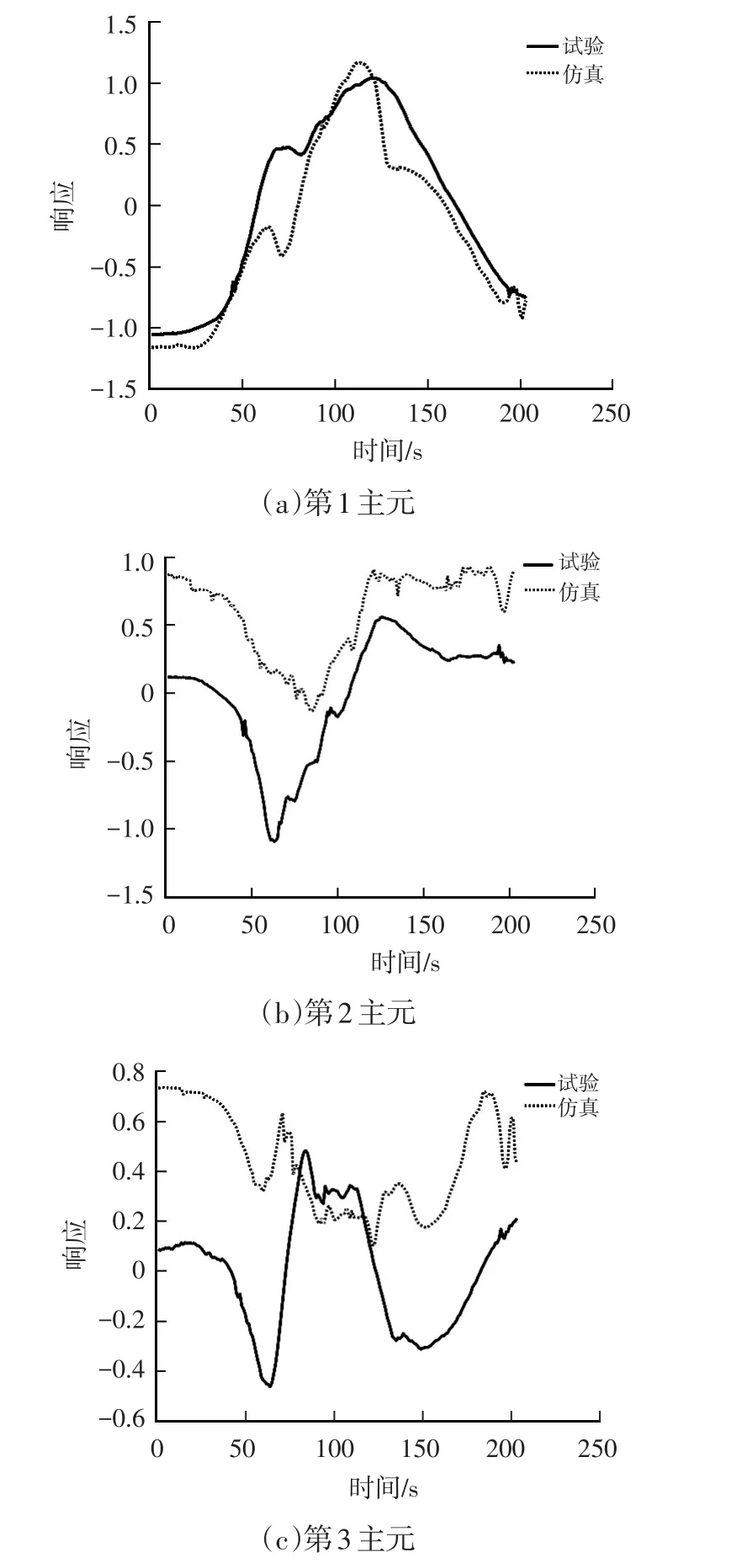
图3　3个主元的时间序列曲线

传统MEARTH方法分析的是时间序列响应本身，而时间序列是由不同频率成分组成的，不同的频率成分重要程度不同，所以需要通过Mallat算法对不同频率成分进行分解和重构，将低频部分重构为近似信号，高频部分重构为细节信号。近似信号可以反映原信号的大致轮廓，细节信号是对信号细节的反映。在汽车的被动安全仿真中，近似信号的重要程度要高于细节信号，所以在对近似信号和细节信号进行评分时，两种信号按不同权值进行组合。图4为第1主元经Mallat分解重构后的信号，由图4可看出，近似信号因缺少高频部分，所以曲线显得更加光滑，而细节信号由高频成分组成，显得非常不规律。因为信号主要以低频成分为主（图5），所以本文只考虑近似信号。

图4　第1主元Mallat分解后的近似信号与细节信号

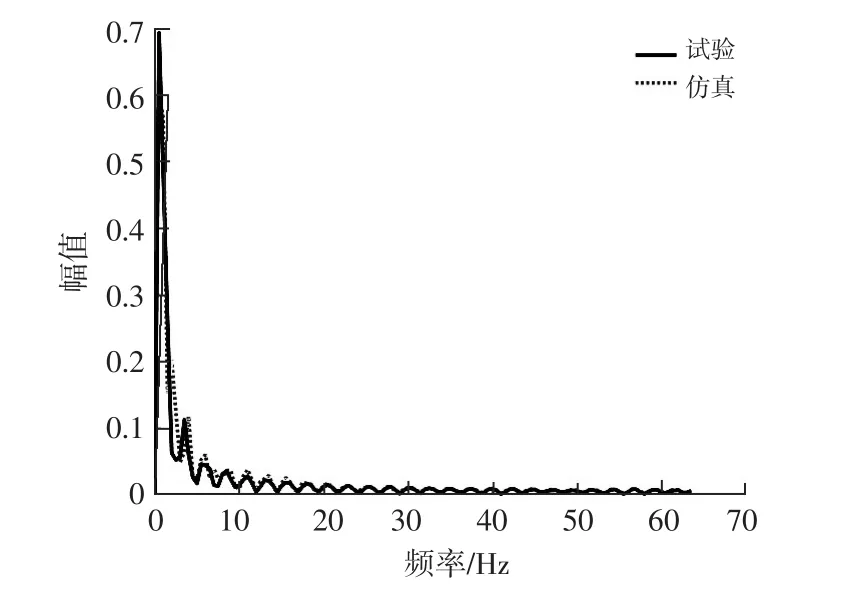
图5　第1主元的傅里叶变化

从幅度误差、相位误差和形状误差3个方面来量化仿真模型的误差。该乘员约束系统仿真模型的各主元的3种误差值见表1。

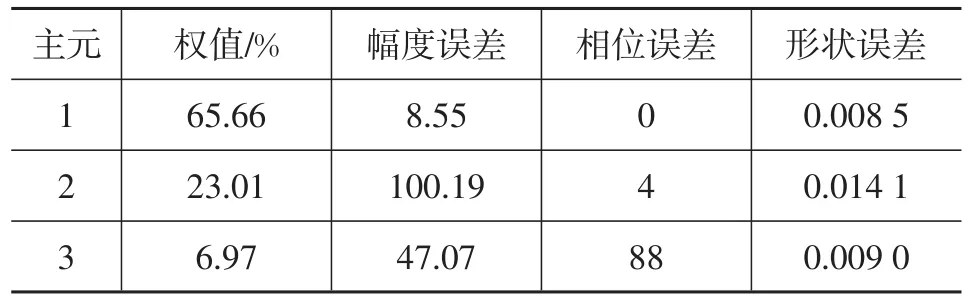
表1　各主元的3种误差值

在得到各主元的3种误差后，依据式（7）计算3种误差的0～100%无量纲评分，再结合专家提供的3种误差的权重系数计算每个主元的误差综合评分。各主元的3种误差的无量纲评分及各主元的综合评分如表2所列。

表2　3个主元的量化误差和评分%

结合图3、表1和表2可知，第1主元通过仿真得到的时间曲线与试验得到的时间曲线吻合较好，因而对应的幅度误差、相位误差和形状误差较小，3种误差的无量纲评分和综合评分较高。而主元3经仿真得到的时间曲线与试验得到的时间曲线吻合较差，因而对应的幅度误差、相位误差和形状误差较大，3种误差的无量纲评分和综合评分较低。由此表明，本文所用的误差评估方法能对仿真模型的输出做出客观的评估。

该组数据通过基于多分辨分析的MEARTH方法计算得到的评分为77.95%，6组数据的评分以及每组对应的传统MEARTH方法评分如表3所列。因为忽略了高频噪声，所以本文所提出方法计算得到的评分要略高于传统MEARTH方法的评分，计算得到的评分方差比传统MEARTH方法的评分方差小18%，证明利用本文所提出方法对模型进行评分更稳定，更能反映模型的本质，比传统MEARTH方法受试验条件变化的影响小。

表3　基于多分辨分析的MEARTH方法与传统MEARTH方法的评分结果对比

得到模型的评分后，通过贝叶斯分类器来对模型是否可以接受进行判断。根据专家经验设置分类器的正类和反类的均值和方差，通过正态随机分布生成训练数据，用训练数据训练分类器，将仿真模型的各响应的综合评分载入到训练好的分类器中，从而判断该组数据所属的类别，即可判断模型的有效性。最终该汽车乘员约束系统模型被归为正类，即该约束条件下仿真模型能以足够的精度代表实际系统。

5　结束语

本文针对模型确认中的多元和动态响应等问题，在传统MEARTH方法的基础上，提出了一种基于多分辨分析的MEARTH方法，并设计了一种基于贝叶斯决策理论的分类器来综合考虑不同响应的模型确认结果，从而可对多元动态系统仿真模型的有效性做出综合评估。通过对某汽车乘员约束系统进行模型确认表明，利用本文所提出方法得到的评分比传统MEARTH方法的评分更稳定，可对多元动态系统仿真模型的有效性做出合理评判。

1Sendur P，Stein J L，Peng H，et al.A model accuracy and validation algorithm，in ASME 2002 International Mechanical Engineering Congress and Exposition，IMECE 2002，2002，pp.573～583.

2Pope N D，Bailey C G.Quantitative comparison of FDS and parametric fire curves with post-flashover compartment fire test data，Fire Safety Journal，2006，41（3）：99～110.

3Geers T L.OBJECTIVE ERROR MEASURE FOR THE COMPARISONOFCALCULATEDANDMEASURED TRANSIENT RESPONSE HISTORIES，in 54th Symposium on Shock and Vibration.，Pasadena，CA，USA，1984，pp.99～107.

4Jiang X，Yang R J，Barbat S，et al.Weerappuli，"Bayesian probabilistic PCA approach for model validation of dynamic systems.SAE International Journal of Materials and Manufacturing，vol.2，pp.555～563，2009.

5Sarin H，Kokkolaras M，Hulbert G，et al.A comprehensive metric for comparing time histories in validation of simulation models with emphasis on vehicle safety applications，in 2008 ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference，DETC 2008，August 3，2008-August 6，2008，New York City，NY，United states，2009，pp.1275～1286.

6Sarin H，Kokkolaras M，Hulbert G，et al.Comparing time histories for validation of simulation models：Error measures and metrics，Journal of Dynamic Systems，Measurement and Control，Transactions of the ASME，vol.132，2010.

7詹振飞.面向汽车安全的不确定性多元动态系统模型验证理论和应用研究：［博士论文］.上海：上海交通大学，2011.

8郑凯，胡洁，詹振飞，等.动态系统模型验证的多元响应分析.上海交通大学学报，2015，49（2）：191～195.

9Zhan Z F，Hu J，Fu Y，et al.Multivariate error assessment of response time histories method for dynamic systems，Journal of Zhejiang University：Science A，vol.13，pp.121～131，2012.

10Yang J，Zhan Z，Chen C，et al.Development of a Comprehensive Validation Method for Dynamic Systems and Its Application on Vehicle Design.SAE International Journal of Materials and Manufacturing，vo l.8，2015.

（责任编辑文楫）

修改稿收到日期为2016年7月31日。

Multiresolution Analysis Based MEARTH Method and Its Application in Automotive Safety Simulation Model Validation

Zhang Yufeng，Zhan Zhenfei，Li Junming
（Chongqing University，Chongqing 400044）

For multivariate and dynamic response in the simulation model validation，a multiresolution analysisbased MEARTH method was proposed，and a classifier based on Bayesian decision theory was designed to consider the validation result of different responses synthetically，thus make a comprehensive evaluation to validity of simulation system of the multivariate dynamic system.The model validation of a vehicle occupant restraint system showed that，rating made by the proposed method is more stable than that made by MEARTH method，and can make a rational judgment of the validity of the multivariate dynamic simulation system.

Multivariate dynamic system,Multiresolution analysis,Automobile safety simulation,Model validation

U461.91

A

1000-3703（2016）09-0013-05