单箱四室箱梁桥剪力滞系数实用计算方法研究

李新平，谢文波，陈清波

（1.华南理工大学土木与交通学院，广东　广州　510641；2.广东省南粤交通投资建设有限公司，广东　广州　510100）

单箱四室箱梁桥剪力滞系数实用计算方法研究

李新平1，谢文波1，陈清波2

（1.华南理工大学土木与交通学院，广东广州510641；2.广东省南粤交通投资建设有限公司，广东广州510100）

介绍了基于能量变分法的单箱四室连续梁桥在恒载作用下中支点截面剪力滞系数的实用计算方法。首先由能量变分法推导箱梁沿梁宽方向的剪力滞系数分布函数，再根据其一般形式假设实用计算函数；利用通用有限元软件Abaqus和结构分析软件MIDAS/Civil分别建立模型，由Abaqus求解出的沿箱梁梁宽方向的弯曲正应力数值解与MIDAS/Civil按初等梁理论计算出的沿梁宽方向的弯曲正应力的比值得出箱梁剪力滞系数，再根据假设的计算函数利用Origin软件拟合得到实用计算公式。结合算例进行复核，论证了推导公式的正确性。

桥梁；单箱四室；剪力滞；能量变分法；函数拟合

根据初等梁理论，箱梁弯曲时翼缘板和底板的正应力是均匀分布的，也就是说在一个截面上同一水平线上的弯曲应力是相等的。但在实际上，翼缘板正应力并非均匀分布，往往沿宽度方向靠近腹板时正应力大些，而远离腹板的正应力逐渐减小。造成这种现象的原因是腹板的约束使翼缘板上的剪应力分布不均匀，导致截面纵向变形不协调而造成翼缘板上面的纵向正应力分布不均匀，这种现象称为剪力滞。以前的桥梁设计中对剪力滞现象考虑较少，导致桥梁在运营过程中出现各种裂缝或其他病害。在近几十年来剪力滞现象越来越受到关注，但还缺乏剪力滞效应计算的实用方法。该文主要研究基于能量变分法的单箱四室梁桥在恒载作用下的剪力滞效应实用计算方法。

1　剪力滞效应的变分解法

利用变分法分析剪力滞是较早采用的一种方法。对于矩形薄壁截面，可用变分法的最小势能原理来分析剪力滞现象。图1为单箱四室截面。

考虑到由于剪力滞的影响，箱梁已不服从初等梁的平截面假定，在描述箱梁翼缘板弯曲位移时，只采用一个广义位移梁的挠度函数ω（x）是不够的，必须再引入纵向位移函数ui（x，y）。悬臂板、翼板、底板位移函数分别为：

图1　单箱四室截面示意图

悬臂板：

式中：ui（x，y）为各箱室翼板和悬臂板的纵向位移； hi为截面形心到顶、底板的距离；uix（）为各箱室翼板和悬臂板剪切转角的最大差值；bi为箱室和悬臂板净宽；

式（2）～（6）中假定翼缘板纵向位移沿横向呈sin函数分布，可知上述公式均能满足变形协调条件。同时在应变能计算时作以下假定：1）腹板仍然采用初等理论计算，不考虑其剪切变形；2）上下翼板竖向无挤压；3）板平面外的剪切变形和横向应变忽略不计。

根据最小势能原理，可得：

梁的外力势能为：

梁的应变能包括腹板、上下翼板的应变能，其中腹板的应变能为：

悬臂板的应变能为：

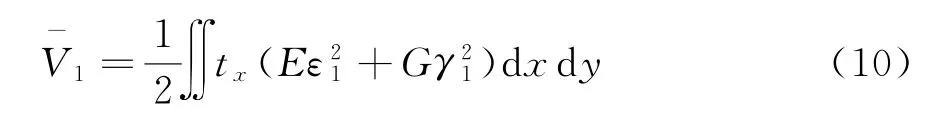
外翼板的应变能为：

内翼板的应变能为：

外底板的应变能为：

内底板的应变能为：

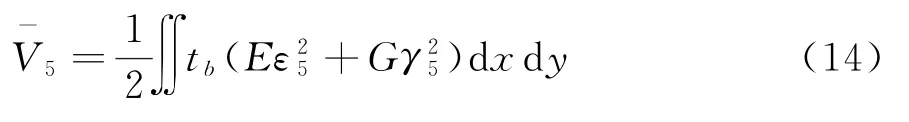
将式（2）～（6）代入式（15），然后代入式（10）～ （14），得：

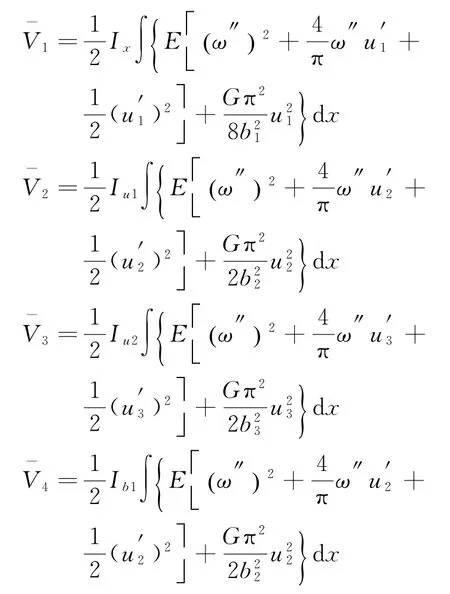
式中：E为弹性模量；G为剪切模量；tu为上翼板厚度；tb为下翼板厚度。

式中：Ix=2txb1h21；Iu1=2tub2h21；Iu2=2tub3h21；Ib1=2tbb2h22；Ib2=2tbb3h22。

根据上述各部分计算体系总势能，得：

式中：Iub1=Iu1+Ib1；Iub2=Iu2+Ib2。

对式（16）进行变分，并令δ∏=0，得到下列微分方程及边界条件：

式中：I=Ix+Iw+Iub1+Iub2。

从式（17）可得：

从而得考虑剪力滞影响的翼板的弯曲正应力，其中悬臂板的弯曲正应力为：

外翼板的弯曲正应力为：

内翼板的弯曲正应力为：

外底板的弯曲正应力为：

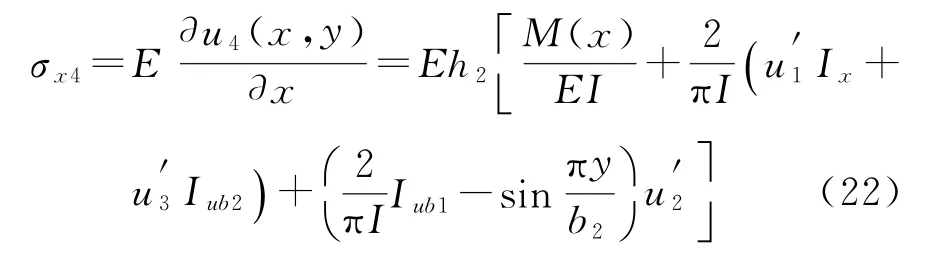
内底板的弯曲正应力为：

2　基于能量变分法的剪力滞效应计算公式

［1]，先利用通用有限元软件Abaqus 和MIDAS/Civil分别求得箱梁各部分弯曲正应力值，利用两者的比值得出箱梁剪力滞系数的数值解，然后由Origin软件依据该数值解拟合假设的函数求出函数中的未知参数。

箱梁影响剪力滞的因素较多，根据前人的研究成果，主要有荷载形式、跨宽比、梁高、翼板程度与厚度、悬臂板长度与厚度、腹板厚度等。由于影响因素较多，先对一些影响参数进行固定，然后利用Origin软件进行函数拟合。

2.1剪力滞系数的数值解

仅将跨径L（L=24、30、36 m）作为拟合的变参数对两跨连续梁桥中支点截面剪力滞效应进行函数拟合，得出针对恒载作用下连续梁桥中支点截面翼板剪力滞效应的实用计算公式。箱梁截面见图1，令翼缘板宽度b2=b3=6 m，悬臂板宽度b1=3 m，梁高H=3.6 m，板厚均取0.4 m。在箱梁上施加均布荷载q=90 k N/m。

利用空间有限元软件Abaqus和结构分析软件MIDAS/Civil分别建立单箱四室箱梁桥模型，求得对应的箱梁各部分弯曲正应力值，然后利用两者的比值求得各剪力滞系数。限于篇幅，这里只列出求解结果。翼缘板和悬臂板的剪力滞系数最值见表1，箱梁在恒载作用下剪力滞系数在梁宽方向的分布见图2～4。

表1　恒载作用下箱梁中支点截面上缘剪力滞系数最值

图2　恒载作用下中支点截面上缘剪力滞系数（L=24 m）

图3　恒载作用下中支点截面上缘剪力滞系数（L=30 m）

从表1、图2～4可知：单箱四室连续箱梁桥在恒载作用下中支点截面上缘沿梁宽方向每个箱室剪力滞系数分布图形相似，且均在翼缘板与腹板交界处出现峰值；中腹板处剪力滞系数稍大于边腹板剪力滞系数，但其差值均在1％以内；随着跨径的增加，剪力滞系数逐渐降低；悬臂板端的剪力滞系数随着跨径增加而增大。

图4　恒载作用下中支点截面上缘剪力滞系数（L=36 m）

2.2待拟合函数选取

由式（19）～（23）可得箱梁各部分剪力滞系数，其中悬臂板的剪力滞系数为：

按初等梁理论，可得：

外翼板的剪力滞系数为：

内翼板的剪力滞系数为：

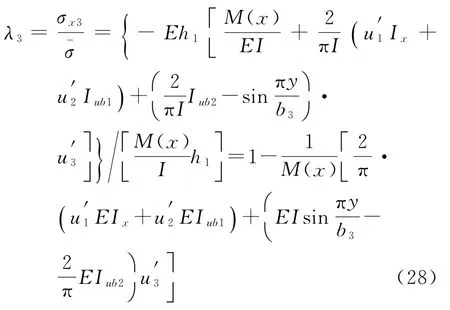
外底板的剪力滞系数为：

内底板的剪力滞系数为：

根据上述分析，单箱四室箱梁桥各箱室的剪力滞系数分布相似。因此，假设差值函数u2（x）= u3（x），同时假设中支点截面最大差值函数随桥梁跨径呈二次抛物线变化。根据其特点对式（26）～ （30）进行简化，得到悬臂板、翼缘板剪力滞系数拟合函数分别为：

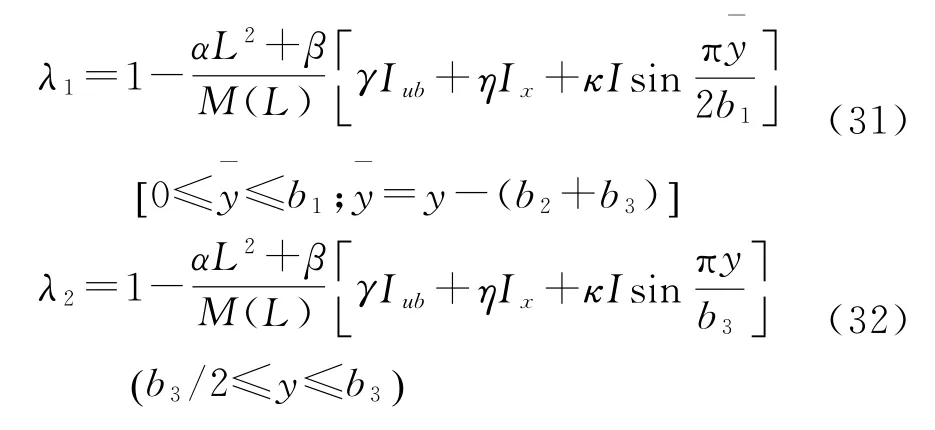
式中：M（L）为中支点截面弯矩（k N·m）；Iub=Iub1+Iub2；α、β、γ、η、κ为待拟合的常数。

2.3函数拟合

利用Origin软件中的自定义函数拟合功能，并根据前述拟合公式进行函数拟合，根据函数拟合结果收敛可求得α、β、γ、η、κ，求得实用计算公式是关于跨径L和整体横坐标y的函数。

根据前述箱梁剪力滞系数的数值解，利用Origin软件拟合得到计算公式，其中悬臂板剪力滞系数的计算公式为：

翼缘板剪力滞系数的计算公式为：

3　算例分析

为验证上述实用计算方法的可靠性，增加跨径L=40 m（其他截面参数同上）的单箱四室梁桥进行分析。利用有限元软件Abaqus和结构分析软件MIDAS/Civil分别建模，求出对应的箱梁弯曲应力值，求两者的比值得出箱梁剪力滞系数分布。同时由上述公式得出计算值，并对软件计算的数值解和公式计算值进行比较。限于篇幅，仅列出比较结果（见表2～4）。

4　结论

（1）两跨单箱四室连续箱梁桥在恒载作用下中支点截面实际剪力滞效应与理论计算结果相符，腹板附近出现剪力滞系数分布峰值，随着离腹板距离的增大而逐渐降低。

（2）两跨单箱四室连续箱梁桥在恒载作用下中支点截面腹板处实际剪力滞系数随着跨径的增加而逐渐减小。

（3）基于能量变分法提出的相应拟合函数并用已经计算出的数据进行拟合，得到了两跨单箱四室连续箱梁的翼板剪力滞系数实用计算公式。由实例计算结果可知该实用计算公式计算结果与数值模拟结果吻合良好，两者差值大部分在5％以内，超出部分也基本在10％以内，满足工程和实际需要。

表2　内翼板剪力滞系数计算结果比较

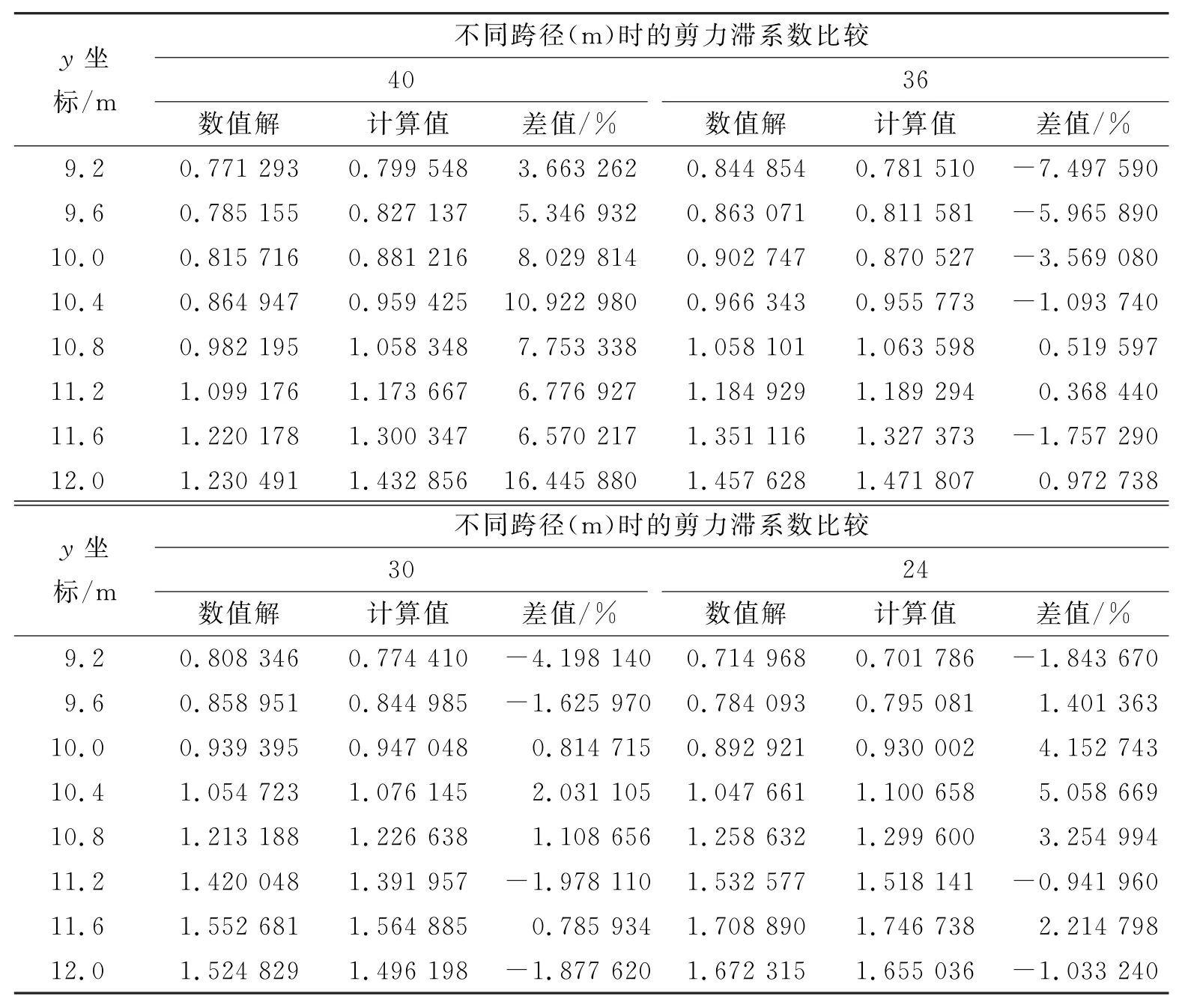
表3　外翼板剪力滞系数计算结果比较

表4　悬臂板剪力滞系数计算结果比较

参考文献：

［1］张士铎.桥梁设计理论［M].北京：人民交通出版社， 1984.

［2］张士铎，邓小华，王文洲.箱形薄壁梁剪力滞效应［M].北京：人民交通出版社，1997.

［3］项海帆.高等桥梁结构理论［M].北京：人民交通出版社，2001.

［4］吴幼明，罗旗帜，岳珠峰.薄壁箱梁剪力滞效应的能量变分法［J].工程力学，2003，24（4）.

［5］徐芝纶.弹性力学（上）［M].第四版.北京：高等教育出版社，2006.

［6］程翔云.梁桥理论与计算［M].北京：人民交通出版社， 1990.

［7］郭金琼.箱形梁设计理论［M].北京：人民交通出版社， 1991.

［8］周若来，沈成武.某高速公路跨线桥裂缝成因分析［J].武汉理工大学学报：交通科学与工程版，2003，27（1）.

［9］罗旗帜，吴幼明.薄壁箱梁剪力滞理论的评述和展望［J].佛山科学技术学院学报：自然科学版，2001，19 （3）.

［10］肖敏，李新平.连续曲线箱梁剪力滞效应分析［J].中外公路，2004，24（4）.

［11］万臻.斜拉桥常用截面形式主梁剪力滞效应研究［D].成都：西南交通大学，2002.

［12］王慧东，强士中.压弯荷载下薄壁箱梁剪力滞效应的变分解［J].北京工业大学学报，2006，32（11）.

［13］曹国辉，方志.薄壁箱梁剪滞效应研究方法［J].湖南城市学院学报：自然科学，2003，24（3）.

［14］姚永丁.独塔单索面斜拉桥箱形主梁剪力滞效应研究［D].杭州：浙江大学，2004.

［15］刘世忠，欧阳永金，吴亚平，等.变截面薄壁箱梁剪力滞剪切变形效应分析［J].中国公路学报，2002，15 （3）.

U448.21

A

1671-2668（2016）01-0170-07

2015-08-03