基于主成分分析和粒子群优化的支持向量机对汽车站客运量的预测

蔡新沧

（福建省城乡规划设计研究院，福建　福州　350008）

基于主成分分析和粒子群优化的支持向量机对汽车站客运量的预测

蔡新沧

（福建省城乡规划设计研究院，福建福州350008）

客运量预测是客运站建设的重要环节，它是反映车站建设规模和生产能力的重要指标。文中通过分析各种已有预测方法的不足，引入主成分分析法和粒子群优化算法对支持向量机进行改进，提出基于改进支持向量机的汽车站客运量预测方法，并通过对漳州市长泰县汽车站客运量数据的分析验证了该方法的有效性。

汽车运输；客运站；客运量；主成分分析；粒子群优化（PSO）；支持向量机（SVM）

汽车客运站作为最重要的公路基础设施，对现代交通的发展起着至关重要的作用。客运量预测是客运站建设的重要环节，它是反映车站建设规模和生产能力的重要指标，也是确定各类设施规模和评定站级的主要依据，研究汽车站客运量的预测方法具有很大的实际意义。

预测客运量的方法有很多，传统预测方法主要有增长率统计法、回归分析法、移动平均法、指数平滑法、弹性系数法、灰色预测法，现代预测方法主要有神经网络、遗传算法、马尔科夫模型、支持向量机、模糊预测。这些方法主要存在两个问题：一是预测精度未达到理想的要求；二是对于回归预测方法中自变量的选取，很多研究只选取几个主要影响因素作为代表，这样虽然降低了分析难度，但有可能将最重要的影响因素忽略，从而使预测结果失真。鉴于当前需求预测中存在的问题，该文采用改进的支持向量机对汽车客运站客运量进行预测，先利用主成分分析法剖析影响因素，从所有影响因素中提取主成分，再利用粒子群优化算法对支持向量机参数进行寻优，使所选择的支持向量机参数更加合理。

1　主成分分析

评价指标可以看成是指标变量，每一变量都不同程度地反映该类指标的信息，变量之间难免存在重叠、相关的关系。在用现代多元统计方法研究多变量问题时，变量太多会增大计算量和增加问题的复杂性，故一般希望在进行定量分析的过程中涉及的变量尽可能少，而信息量尽可能多。主成分分析是解决这一问题的理想工具。

假设有n个指标X1，X2，X3，…，Xn，分别表示每个对象的各种特性，如果有N个对象，则可用N ×n矩阵表示，即：

按下式进行标准化处理，生成标准化矩阵Y：

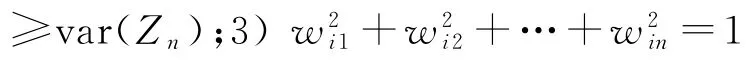
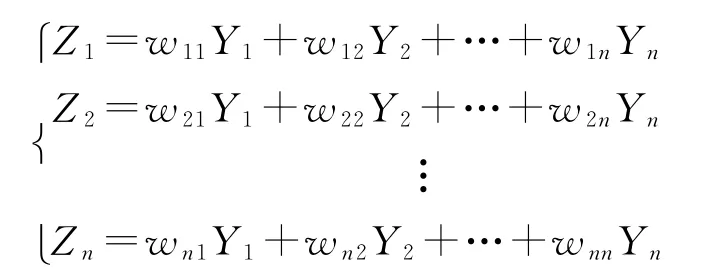
计算主成分的方法是首先计算标准变量的自相关矩阵R=E（YY）T，然后计算自相关矩阵的特征值λ1，λ2，…，λN及相应的特征向量q1，q2，…，qN。主成分值相当于将标准变量Y向随机向量q投影，即A=YTq，则特征值越大对应的特征向量越重要，根据累计贡献率或指定主要特征的个数提取最大的特征向量。

2　基于PSO算法的SVM参数选择

支持向量机（Support Vector Machines，SVM）是一种基于统计学习理论的机器学习方法，能较好地解决小样本、非线性等实际问题。通常采用既直观又简单的试验定参法（通过大量试验）获得较优的参数，但该方法费时，且获得的参数不一定最优。

粒子群优化（Particle Swarm Optimization， PSO）算法是群体智能的一个新分支，源于对鸟群捕食行为的研究。粒子在寻优过程中，每个优化问题的解均被认为是搜索空间中的一个粒子，每个粒子都根据适应度函数计算其适应值，且每个粒子有一个速度，它们决定粒子飞翔的方向和距离，每次迭代中粒子根据个体最优值和全局最优值更新。

该文采用基于PSO算法的SVM参数选择方法对汽车客运站客运量进行预测。文献［3]、［4]详细描述了粒子群算法的寻优原理，文献［5]～［7]描述了粒子群优化支持向量机参数的选择步骤，在此不详述。

3　基于改进支持向量机的客运量预测

（1）研究对象影响因素确定。首先确定汽车站客运量的影响因素，它是进行主成分分析的前提。

（2）研究对象和影响因素的标准化。对汽车站客运量及各种影响因素进行标准化，以消除量纲对预测结果所带来的影响。

（3）影响因素主成分分析。对确定好的影响因素进行主成分分析，提取主成分，为支持向量机回归作准备。

（4）构造样本集。以提取的主成分作为输入，标准化后的研究对象作为输入，进行支持向量机的学习。在整个学习过程中，利用粒子群优化的方法进行参数寻优，从而获得最佳的支持向量机参数。

（5）支持向量机的预测及对预测结果的评价。利用学习获得的最佳参数进行支持向量机预测，对预测结果进行反标准化处理，同时进行评价。

4　实例分析

以漳州市长泰县汽车站客运量预测为研究对象，将2004—2010年的客运量数据作为训练样本、2011—2013年的客运量数据作为预测样本。

4.1影响因素的确定

确定影响因素是进行准确回归分析的基础。选取9个汽车站客运量影响因素进行分析，分别为国内生产总值X1、第一产业贡献率X2、第二产业贡献率X3、第三产业贡献率X4、长泰县总人口X5、城镇人口X6、农村人口X7、长泰县汽车保有量X8、平均运距X9。长泰县汽车站2004—2013年客运量及各影响因素的数据见表1。

表1　2004—2013年长泰县汽车站客运量及各影响因素的数据

4.2汽车站客运量和指标的标准化

利用SPSS软件对10个变量进行处理，结果见表2。根据表2中的均值和标准差，按式（1）计算，得到各指标的标准化值。

表2　SPSS软件处理结果

4.3主成分分析

根据表3所示因子系数矩阵，建立两个主成分的因子得分模型如下：

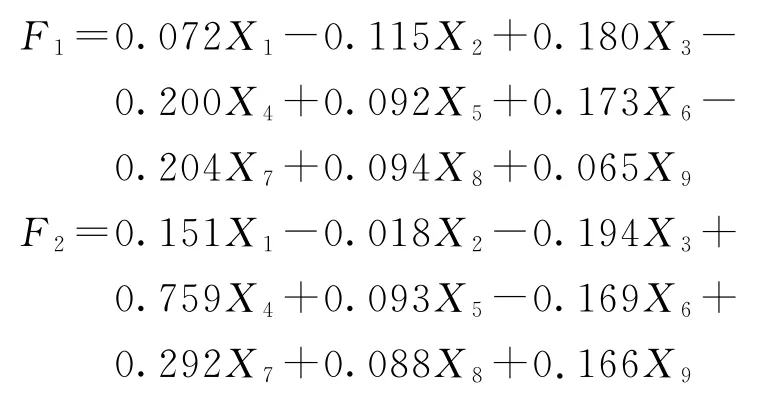
4.4客运量预测与结果评价

根据主成分分析模型构造学习样本集，利用libsvm加强工具箱进行粒子群优化的支持向量机学习。表4为基于主成分分析和粒子群优化的支持向量机的预测结果及与未进行主成分分析的粒子群优化的支持向量机预测结果的对比。

从表4可以看出：与传统的支持向量机相比，基于主成分分析法和粒子群优化算法的支持向量机具有更高的预测精度、更好的应用效果。

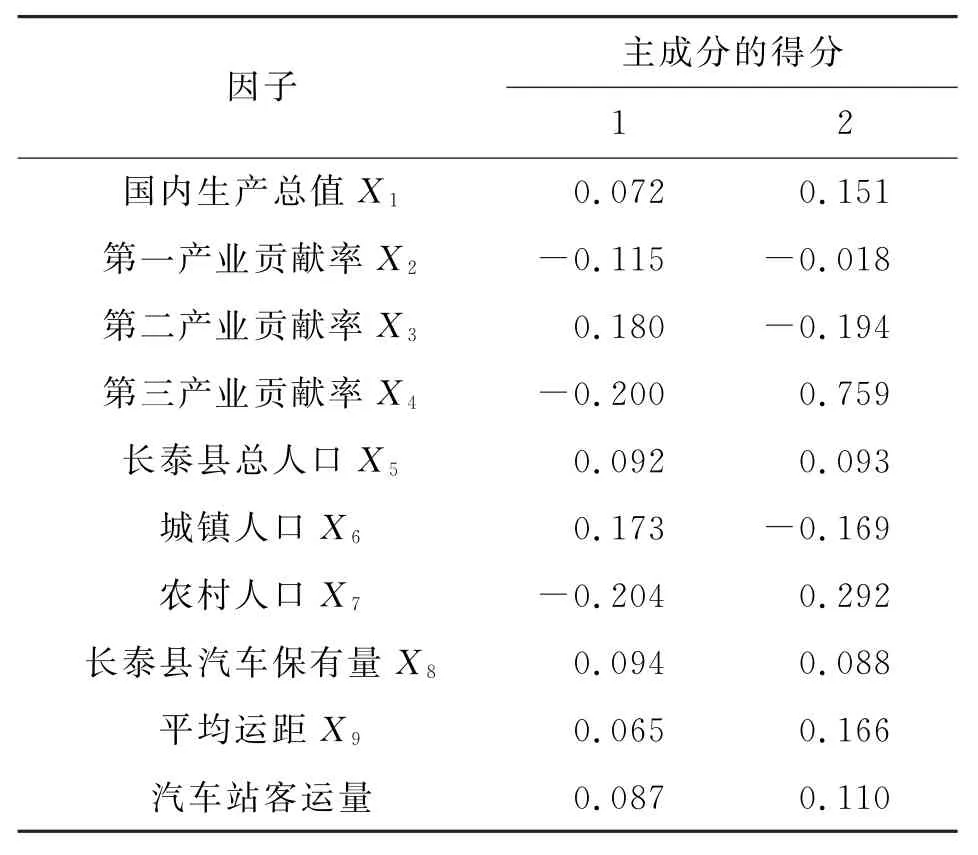
表3　因子得分的系数矩阵

表4　2011—2013年长泰县汽车站客运量预测结果对比

5　结论

该文采用基于主成分分析法与粒子群优化算法的支持向量机进行汽车站客运量预测，一方面，主成分分析法的使用不仅全面考虑了影响客运量的因素，同时降低了统计分析的难度；另一方面，粒子群优化算法的全局寻优特性实现了对支持向量机参数的快速寻优及精确预测。对漳州市长泰县汽车站客运量数据的分析结果表明，该预测方法的精度比以往预测方法的高，能得到令人满意的结果，适用于汽车站客运量预测。

［1］武志鹏.汽车站客运量预测及客商结合模式研究［D].西安：长安大学，2012.

［2］孙占全，潘景山，张赞军，等.基于主成分分析和支持向量机的交通流预测［J].公路交通科技，2009，26（5）.

［3］张利彪.基于粒子群优化算法的研究［D].长春：吉林大学，2004.

［4］邵信光，杨慧中，陈刚.基于粒子群优化算法的支持向量机参数选择及其应用［J].控制理论与应用，2006，23 （5）.

［5］刘逸.粒子群优化算法的改进及应用研究［D].西安：西安电子科技大学，2013.

［6］古文成，柴宝仁，滕艳平.基于粒子群优化算法的支持向量机研究［J].北京理工大学学报，2014，34（7）.

［7］陈建胜.基于粒子群优化算法的支持向量机集成学习方法研究［D].杭州：杭州电子科技大学，2009.

［8］吴欢.基于改进支持向量机的深基坑变形预测模型研究［D].南昌：江西理工大学，2013.

［9］李楠，石超峰.基于粒子群算法优化支持向量机的公路客运量预测［J].公路与汽运，2014（4）.

［10］武志鹏.汽车站客运量预测及客商结合模式研究［D].西安：长安大学，2012.

［11］孙占全，潘景山，张赞军，等.基于主成分分析与支持向量机结合的交通流预测［J].公路交通科技，2009， 26（5）.

［12］彭珍瑞，孟建军，祝磊，等.基于支持向量机的铁路客运量预测［J].辽宁工程技术大学学报，2007，26（2）.

U492.1

A

1671-2668（2016）01-0071-03

2015-09-07