基于支持向量机和参数在线优化的锅炉燃烧系统

陶成飞，王明春，唐志炳，刘劲权

(东南大学能源与环境学院，南京　210096)

基于支持向量机和参数在线优化的锅炉燃烧系统

陶成飞，王明春，唐志炳，刘劲权

(东南大学能源与环境学院，南京210096)

介绍了最小二乘支持向量机的基本概念，提出了锅炉燃烧参数在线优化的模型及步骤。利用某锅炉热态实验的数据对模型进行了校验。研究结果表明:采用参数在线优化技术和最小二乘支持向量机方法建立的锅炉燃烧模型能够很好地跟踪燃烧系统的时变特性，并且具有泛化能力好、计算速度快的特点。

自适应;燃煤锅炉;燃烧优化;最小二乘支持向量机

作为一种近年发展起来的新型机器学习方法，最小二乘支持向量机(LSSVM)应用结构风险最小化原则，有效地解决了小样本、非线性、高维数等实际问题。标准情况下的支持向量机(SVM)建模需要求解一个受约束的二次型优化问题，得到全局最优点，解决局部极小值问题，但所需要的核函数空间随着样本的增大而增大，算法的实现程度困难。为了减小SVM的计算复杂度，Suykens提出了LSSVM，能够将机器学习问题转化为解线性方程组问题，其拓扑结构只与支持向量有关，减小了计算量，达到较快的计算速度，更适用于在线优化。参数在线自适应优化技术是基于LSSVM的方程组问题提出的，根据KKT(Karush-Kuhn-Tucker)定理［1］，在拉格朗日函数的鞍点有KKT互补条件成立，通过KKT互补条件很容易求解拉格朗日函数的问题。

笔者提出了一种基于LSSVM和参数在线自适应优化技术的锅炉燃烧优化控制系统，构造了以锅炉效率和NOx排放为组合的大型四角切圆燃烧锅炉的回归模型，从DCS上采集数据，并且对该模型进行了在线训练和校验，使用参数实时在线更新技术对KKT的互补条件进行数据实时更新，使LSSVM模型参数不断更新，适应燃烧过程中锅炉时变的特性，从而达到燃烧优化的目的。

1　最小二乘支持向量机

1.1用于回归问题的支持向量机算法

SVM采用最优分类面的方法，将分类问题转化成一个凸二次规划问题，应用拉格朗日函数对凸二次优化问题求解。SVM的主要优点在于它的泛化能力好，适合于小样本的学习［2］。对于样本集，xi∈Rn为输入量，yi∈Rn为输出量，i=1，2，…，k，支持向量回归(SVR)算法寻求最优的函数f(x)=(w·x)+b，w∈Rn，b∈R，其中b为常数;从而使得预测的期望风险最小，为结构风险，代表模型的复杂度，为经验风险，代表回归模型的误差，C为松弛因子，用于在结构风险和经验风险之间的平衡。

定义核函数K(xi，xj)=Φ(xi)·Φ(xj)。常用的核函数形式有线性、多项式、径向基等，一般采用径向基函数(RBF):

式中:σ为核宽度，反映了边界密封包含的半径。

非线性回归函数就可以表示为:

应用此方法建模，核函数空间太大，拉格朗日系数二次规划求解复杂，所以笔者采用了最小二乘法解决二次规划的问题。

1.2最小二乘支持向量机

利用高维特征空间中的线性函数y(x)= WTΦx+b来拟合样本集。根据结构风险最小化原理，综合考虑函数复杂度和拟合误差，回归问题可以表述为约束优化问题［3］。

使用拉格朗日函数把上述约束优化问题变成无约束优化问题:

式中:W和WT分别表示空间向量及其对称矩阵; w表示输入样本集。由KKT条件可以得到:

2　基于参数在线优化技术的燃烧模型

2.1锅炉燃烧在线优化模型

燃煤锅炉的优化通过提高锅炉效率和降低NOx的排放来实现，在DCS控制系统中寻找最优的设定点来控制操纵变量Vm，从而达到优化模型的目的。燃烧模型是用来描述控制变量和系统输入变量之间的联系，系统输入变量包含操纵变量Vm和扰动变量Vd，其中Vm包含氧量、二次风开度以及其他可调节变量，Vd指来自其他系统的不可变参数，如机组负荷变化等。

锅炉效率η通过ASME(美国机械工程师协会)制定的锅炉效率计算模型来确定，因此寻找最优操纵变量Vm可以通过求解优化方程来解决［4］;w1、w2分别是关于经济目标和环境目标的权值;［Vm］min和［Vm］max指操纵变量的优化范围。由于模型的结构复杂，锅炉的燃烧优化通常通过非线性优化技术，常用的有遗传算法(GA)、粒子群算法(PSO)等。优化方程为:

式中:w(NOx)为烟气中NOx的质量分数，%。

2.2最小支持向量机参数在线优化原理

根据统计学习方法［5］，LSSVM模型可以用下式表示:

其中k(x，xi)表示核函数。

根据式(11)，最初的LSSVM训练模型需要计算H矩阵的逆矩阵H－1，由于H是对称矩阵，所以它的逆矩阵存在。如果训练集过大，计算量随之增加，式(12)需要的模型训练时间会延长，因此，最初的模型训练算法不适用于在线更新。特征矩阵H每更新一次只有一行和一列参数发生变化，变化前后的逆矩阵H－1相关性较大，这种数学关系和模型更新方法采用文献［4］使用的矩阵变换法。

假设最初训练集有l组样本，在更新过程中，先将第i个支持向量(xi，yi)被新的操作参数(xj，yj)替换，再将特征矩阵H的i行与j行互换，得到矩阵H－1，然后再将H－1的i列与j列互换，得到的新矩阵H1。

根据矩阵的理论，从矩阵H到H1可以通过在矩阵H前后分别乘以单位向量和矩阵，即。连续在线自适应参数更新过程是用新的操作数据(xj，yj)代替H中旧的支持向量(xj，yj)，得到H2，H2可表示为:

回归模型参数优化后的新模型H2的参数α'和b'见式(15)，y'是新的回归模型H2训练集的输出量，它是先由yi与yl对换，再将yi替换为yj得到。优化后回归模型输出y'=［y1，…，yi－1，yl，yi+1，…，yl－1，yj］。

通过改变SVM回归模型的拓扑结构，并且使用第l个支持向量(xl，yl)替换第i个支持向量(xi，yi)，从而完成了模型在线自适应更新过程。

2.3燃烧参数在线优化的步骤

锅炉燃烧参数在线优化步骤是:

(1)选取参数C和σ的寻优范围、初值、各自步长。

(2)从总样本选取第i(i=1，2，…，l)份作为测试样本。剩余l－1份作为训练样本。分组数即为l，利用训练样本训练LSSVM。

(3)对于新的训练值xj，计算出它的回归模型输出Yj，将Yj与实际输出值yj比较，并计算回归误差ε，如果回归误差ε=|(yj－Yj)/yj|小于设定的临界值εc，则进入第(4)步，否则进入第(5)步。

(4)如果回归误差在规定的范围内，所建立的回归模型有效，比较所有误差率的平均值，取误差率最小时所对应的参数为最优参数。

(5)模型的精度不够时，在原来的支持向量(xi，yi)中寻找最接近新的操作参数(xj，yj)的一项，重复步骤(3)。

(6)结合新的操作参数(xj，yj)，计算矩阵H1、H2及相关的中间量。

(7)用训练集矩阵中的l元素替换i元素，再用新的输出值yj替代l，获得的新输出支持向量可以表示为:

(8)假定e是所有元素都为1的l维向量，结合H2－1和y'，计算新的模型参数α'和b'。(9)持续使用最新的操作参数来替代最初参数来更新LSSVM回归模型的训练集。

通过比较LSSVM回归模型的输出值和系统的实际输出值来决定是否需要采用参数在线优化。

3　仿真实验与结果分析

3.1实验样本的获取

利用文献［2］提供的现场试验工况数据，分别建立NOx排放特性的响应模型。实验锅炉蒸发量为1 160 t/h，主蒸汽温度为540℃，压力为16.82 MPa，配用350 MW的凝汽式发电机组。锅炉采用直吹式磨煤系统，四角切圆燃烧锅炉。实验数据一共96组，全负荷50组，90%负荷20组，80%负荷20组，70%负荷6组。燃烧工况为纯煤燃烧和煤粉与BFG混烧，ED层二次风为BFG配风，GG到KK层均为煤粉配风，其中KK层在最上层作为燃尽风。现场实验数据见表1。

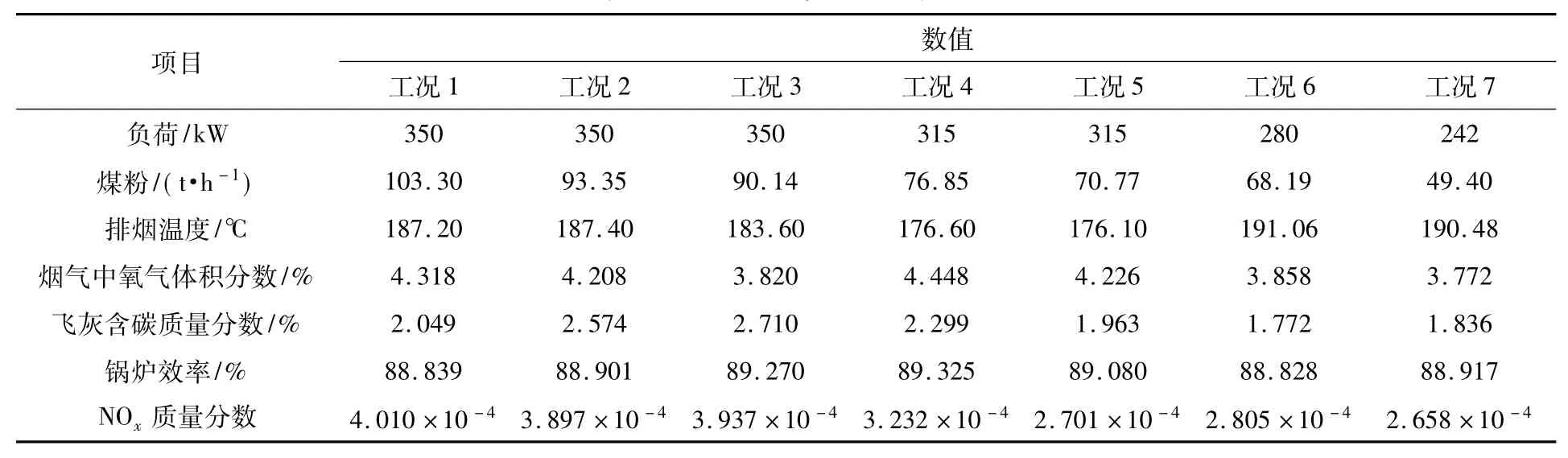
表1　现场实验工况数据

3.2模型输入变量的选取

以锅炉NOx排放量为例，选取影响锅炉NOx排放特性的运行参数，如锅炉负荷、床温、一次风、二次风等18个为输入量，应用LSSVM建立了以NOx排放为输出的模型，随机选取43组数据作为训练数据。为了使每个输入量对LSSVM的影响相同，将输入样本作归一化处理，处理后的输入和输出数据均落在［0，1］。

3.3仿真结果

采用SVM建模时，选择径向基函数K(xi，xj) =exp(－|xi－xj|2/2σ)为核函数。在核函数确定的情况下，惩罚系数C和核参数σ决定了模型的样本误差、复杂度和泛化能力，其中C和σ的寻优范围分别为(0，1 000)和(0，100)。根据设定的训练数据，利用K-fold交叉验证方法，通过不断调整各个参数的值进行循环搜索优化，其中K=10。

按照上述方法，通过在线自适应寻优后，得到的LSSVM最佳参数组合为C=1 000，σ=0.45。带入SVM中，由53组训练数据建立NOx排放模型，剩下的43组测试数据对NOx排放量模型进行预测，仿真结果见图1。由图1可知，LSSVM在线优化模型能够对测试数据很好地拟合。

为了验证模型的泛化能力，将43组测试数据进行NOx排放量预测(见图2)。

由图2可以发现，模型的样本预测值几乎与真实值一致。预测误差显示，检验样本的预测误差几乎都≤5%，足以说明LSSVM参数在线优化模型能够对NOx的排放精确预测，因此该模型具有较好的泛化能力(见图3)。

综上所述，对于本文的研究对象而言，在线参数优化LSSVM模型的泛化能力较强，预测精度较高，能够很好地满足电站锅炉燃烧的大时滞和大惯性特征。

4　结语

由以上分析可知:

(1)针对锅炉燃烧这一复杂的非线性系统，笔者采用一种参数在线更新技术，通过不断优化锅炉NOx燃烧模型的最小支持向量来预测锅炉的排放，实验和仿真结果显示该优化技术能够很好地满足锅炉燃烧的时变特性，同时大大减少了运算时间和计算量。

(2)煤质的不同会显著影响锅炉的燃烧过程，然而由于煤质的复杂特性，传统技术很难测定煤质对锅炉燃烧的影响，并且测试的技术还很不成熟，价格昂贵。笔者提出的在线参数优化技术，当煤的特性发生变化的时候，能够及时调节燃烧模型参数，从而提高燃烧效率。

(3)为了获得完整的锅炉燃烧参数，现实中常常进行锅炉燃烧调整实验，实验周期长，成本高，并且影响机组的正常运行，使用基于LSSVM的参数优化技术，可以直接利用电厂DCS系统的历史数据，减少了燃烧试验的次数。

(4)当锅炉的煤质和其他运行条件发生变化时，可以重新训练LSSVM，该系统能够有效地提高电厂的运行水平，具有很大的推广应用价值。

［1］王春林，周昊，周樟华，等.基于支持向量机的大型电厂锅炉飞灰含碳量建模［J］.中国电机工程学报，2005，25(20): 72-76.

［2］安恩科，宋尧，杨霞.基于支持向量机和遗传算法的燃煤电站锅炉多目标燃烧优化［J］.节能，2008(10):22-25.

［3］麻洪波，牛培峰，李国强，等.基于GSA-SVM的循环流化床锅炉NOx排放特性模型［J］.计量学报，2013，34(6): 602-606.

［4］Gu Y P，Zhao W J，Wu Z Z.Online adaptive least squares support vector machine and its application in utility boiler combustion optimization systems［J］.Journal of Process Control，2011，21(7):1040-1048.

［5］马丽丽，黄仙.支持向量机回归算法在锅炉燃烧系统建模中的应用研究［J］.现代电力，2008，25(2):72-75.

［6］饶苏波.多目标进化算法在电站锅炉燃烧优化控制系统设计中的应用［J］.广东电力，2006，19(4):11-15.

An Optimized Boiler Combustion System Based on LSSVM and Online Parameter Optimization

Tao Chengfei，Wang Mingchun，Tang Zhibing，Liu Jinquan
(School of Energy and Environment，Southeast University，Nanjing 210096，China)

The basic concept of least squares support vector machine(LSSVM)is introduced，and the model and procedures for online optimization of boiler combustion parameters are proposed，which is calibrated using hotstate experimental data of a boiler.Results indicate that the boiler combustion model established based on online parameter optimization and LSSVM is able to trace the time-variant characteristics of the boiler combustion system，with good generalization ability and high calculation speed.

self adaption;coal-fired boiler;combustion optimization;LSSVM

TK223.7

A

1671-086X(2016)01-0016-05

2015-07-15

陶成飞(1991—)，男，在读硕士研究生，研究方向为热工自动化。

E-mail:1011942531@qq.com