基于结构方程模型的卷烟企业关键质量特性识别研究*

于洪基

(中共许昌市委党校，河南 许昌 461000)



基于结构方程模型的卷烟企业关键质量特性识别研究*

于洪基

(中共许昌市委党校，河南 许昌 461000)

由于卷烟企业的生产过程是一个多级的过程，多级的生产过程的质量控制具有复杂性，所以传统的识别方法很难取得有效的识别结果。采用结构方程的方法可以解决这个问题。结构方程能够同时处理多个因变量、允许自变量和因变量含有测量误差，并能根据拟合优度指数对原有模型进行修正。通过一个具体的实例来进行卷烟企业关键质量特性的识别研究。

关键质量特性;结构方程;主成分分析

卷烟企业的生产过程是一个自动化程度很高的多级生产过程，对于多级生产过程来说，每一道工序都产生质量波动，这些质量波动会直接或间接影响到后续工序。在卷烟生产过程中，其各个工序如原材料、嘴棒、制丝和卷包等输出的质量波动会迅速传递到最终产品的质量特性中。卷烟生产中某一个工序出现了错误都会反映到最终的产品质量上，卷烟产品的质量性能取决于各级过程的累积效应。

在卷烟企业的质量管理中，由于卷烟产品生产过程存在多种产品质量相互影响、多个质量特性相互作用、产品质量相互传递等现象，因此多个质量特性的协同控制成为保证产品质量的一个重要方面。[1]生产过程的关键质量特性是指在零部件和原材料加工制造及装配过程中影响其加工制造质量、装配质量及制造过程质量的少数关键技术、操作及装配等的集合。[2]在卷烟生产过程中的质量特性之间存在相关性，由于成本及效率的关系，无法对全面质量特性进行监控。因此在卷烟企业的质量控制和改进中，需要通过寻找关键的质量特性进行优化和控制。也就是需要对影响原材料、嘴棒、制丝和卷包等生产过程的关键质量特性进行识别。

当输入变量和输出变量都有多个的时候，且这些变量存在自相关关系或这些变量无法直接测量的时候，传统的关键质量特性识别方法，如QFD、因子分析等，在进行识别的时候常常会失效。[3]基于此，本文利用结构方程模型的方法对卷烟企业生产过程中关键质量特性进行识别。

一　结构方程模型

(一)结构方程的结构

结构方程模型是通过变量协方差矩阵、相关系数矩阵来分析变量之间关系。在经济学和管理学等专业研究中，很多变量都无法直接测量，例如研究客户认知的时候，客户期望、客户感知等变量无法直接测量，这些变量可以称为潜变量。对于这些潜变量，设置一些显变量，利用这些显变量间接测量潜变量，通过这些测量指标来进行问卷调查的设计。[4]传统的统计方法无法对潜变量进行测量，结构方程模型则可以通过测量显变量来反映潜变量，而且结构方程允许这些测量变量还有测量误差。

结构方程模型可分为结构方程和测量方程两部分。结构方程模型的各个指标会含有随机误差和系统误差。随机误差指由于测量的不准确导致的误差，系统误差则指测量本身含有的误差。

1.测量模型。对于指标与潜变量(例如六个财务指标与公司盈利能力)之间的关系，则写成如下测量方程：

x=Λxξ+δ；y=Λyη+ε

其中，x为外源指标( Exogenous Indicators) 组成的向量。

y为内生指标( Endogenous Indicators) 组成的向量。

Λx为外源指标与外源潜变量之间的关系，称为外源指标在外源潜变量上的因子负荷矩阵。

Λy为内生指标与内生潜变量之间的关系，称为内生指标在内生潜变量上的因子负荷矩阵。

ξ为外源潜变量，即模型中不受其他变量影响但影响他人的变量。

η为内生潜变量，即模型中会受到任何一个其他变量影响的变量。

δ为外源指标x 的误差项。

ε为内生指标y 的误差项。

2.结构模型。对于潜变量之间的关系，则可写成如下结构方程：

η=Bη+Γξ+ζ

其中，B为内生潜变量间的关系。

Γ为外源潜变量对内生潜变量的影响。

ζ为结构方程的残差项，反映了η在方程中未能被解释的部分。

(二)结构方程的建模过程

结构方程模型主要作用就是研究各个潜变量之间的结构关系，模型建立的首要条件就是设定潜变量。根据测量指标与潜变量之间的关系不同分为两种情况处理。[5]首先，如果在具体的实例中对于测量指标与潜变量之间的关系很清楚，研究人员就可以据此来确定潜变量的数量以及潜变量之间的关系，并可以先建立一个虚拟的结构方程模型。其次，如果测量指标与潜变量之间的关系并不清楚，不能据此来确定潜变量的数量，我们可以利用主成分分析(PCA)的方法对测量指标进行降维，来提取出测量指标的主成分。先对提取数据的样本进行整理，然后分析数据的信度和效度。如利用SPSS对测量指标x1、x2、x3、x4、x5、x6、y1、y2、y3、y4进行主成分分析，提取出四个主成分。即我们可假定ξ1、ξ2为外源潜变量，η1、η2为内生潜变量，且x1、x2、x3为ξ1的测量指标，x4、x5、x6为ξ2的测量指标，y1、y2为η1的测量指标，y3、y4为η2的测量指标。[6]可建立起如图1所示的一个结构方程初步模型。

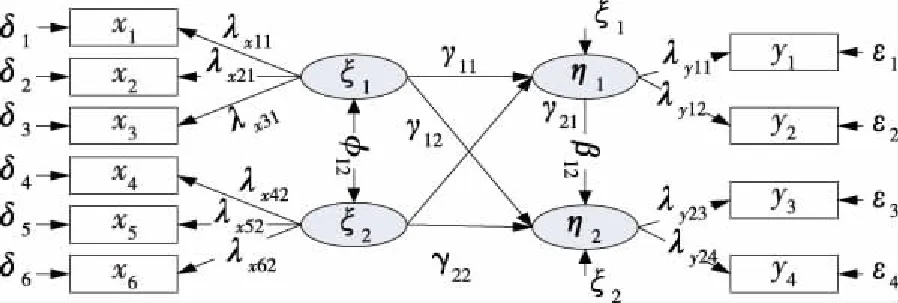
图1　结构方程概念模型

图1中ξ1、ξ2为外源潜变量，η1、η2为内生潜变量，δ1、δ2、δ3、δ4、δ5、δ6、ε1、ε2、ε3、ε4为对应指标的测量误差，λx11、λx21、λx31、λx42、λx52、λx62、λy11、λy21、λy32、λy42为指标在对应潜变量上的因子负荷，φ21表示外源潜变量ξ1、ξ2之间的相关性，γ11、γ12、γ21、γ22表示外源潜变量ξ1、ξ2对内生潜变量η1、η2的影响，β21为内生潜变量η1对η2的影响，ζ1、ζ2分别为内生潜变量η1、η2的残差。

根据求得数据的协方差矩阵或相关系数矩阵，利用结构方程模型的相关软件，如LISREL，Mplus，AMOS，同其他同类型的统计软件相比，LISREL功能相当强大，但是操作起来难度较大。[7]软件运行之后可得到结构方程的路径图。最后需要对结构方程模型进行拟合优度估计，根据拟合优度指数对模型进行修正。

二　卷烟企业的实例分析

本文对某卷烟企业的制丝车间、嘴棒车间、卷包车间中的12个指标即整丝率、碎丝率、填充值、纯净度、嘴棒硬度、嘴棒吸阻、卷烟圆周、水分、嘴棒圆周、卷烟硬度、卷烟单支重量、卷烟吸阻等进行连续的抽样测量，得到了测量数据。

由于对于潜变量的个数和潜变量与测量指标之间的关系难以确定，我们首先先对数据进行主成分分析，确定潜变量个数和潜变量与测量指标之间的关系。把已经得到的数据输入SPSS中，进行主成分分析，得到如下的分析结果(见表一)。

表一　解释的总方差

提取方法：主成份分析。

由表一可知从这12个指标中提取了四个主成分，有四个特征值大于1。从表中看到，第一个主成分的特征值为4.947，方差贡献率为41.221%，第二个主成分的特征值为2.485，方差贡献率为20.710%，第三个主成分的特征值为1.356，方差贡献率为11.296%，第四个主成分的特征值为1.203，方差贡献率为10.026%，累积方差贡献率为83.254%，即四个主成分共解释了总变异的83.254%，说明提取四个主成分是合适的。把四个主成分命名为烟丝质量、嘴棒质量、卷烟外观质量、卷烟内在质量。

关于结构方程的软件有很多种，本文使用LISREL软件进行模型训练。将整理好的输入到LISREL软件中，运行后得到如图2所示的路径图。

图2　采用LISREL软件分析得到的路径图

图2中烟丝质量、嘴棒质量为外源潜变量，碎丝率、纯净度、整丝率、水分、填充值、嘴棒硬度阻、嘴棒吸为其外源指标。卷烟嘴棒质量、卷烟外观质量为内生潜变量，卷烟圆周、嘴棒圆周、卷烟单支重量、卷烟吸阻、卷烟硬度为内生指标。

根据图2可得出如下的卷烟企业的结构方程模型。

(1)

(2)

(3)

其中(1)、(2)为测量方程，(3)为结构方程。

从图2的路径图可以分析一下关于卷烟企业生产过程的特点：

1.碎丝率为影响烟丝质量的关键质量特性。是由于碎丝率对烟丝质量的因子载荷的绝对值最大，所以碎丝率是烟丝质量的关键质量特性。

2.嘴棒吸阻为影响嘴棒质量的关键质量特性。是由于嘴棒吸阻对嘴棒质量的因子载荷的绝对值最大，嘴棒吸阻为影响嘴棒质量的关键质量特性。

3.嘴棒圆周为影响卷烟外观质量的关键质量特性。

4.卷烟硬度为影响卷烟内在质量的关键质量特性。

三　结　语

本文运用结构方程模型来对制造行业的生产过程的关键质量特性识别进行研究，在国内还属于较新的研究，以往的研究多是运用QFD等方法来进行，利用QFD方法识别出的关键质量特性也不够准确。[8]从本文的实证分析的过程可以看出，结构方程模型在识别关键质量特性方面更具有优势，使卷烟企业及制造型企业的质量控制更加精确，对于自动化程度很高的制造企业来说，可以使质量控制成本得到有效的节约，有利于提高中国制造业的产品质量。

[1]Flynn,B.B.,Flynn,E.J.Synergies between supply chain management and quality management: emerging implications [J].International Journal of Production Research,2005,43(16): 3421-3436.

[2]Yao,Y.and Gao,F.A survey on multistage/multiphase statistical modeling methods for batch processes [J].Annual reviews in control,2009,33:172-183.

[3]Pearn,W.L.,Chang,C.S.Precision measures for processes with multiple manufacturing lines [J].International Journal of Advanced Manufacturing Technology,2006,30: 1202-1210.

[4]侯杰泰,温忠麟,成子娟.结构方程模型及其应用[M].北京：教育科学出版社，2004:7.

[5]侯杰泰,成子娟.结构方程模型的应用及分析策略[J].心理学探新,1999,19 (1):54-59.

[6]多级生产过程中关键质量特性的识别研究[D].郑州大学硕士论文,2013.

[7]何桢,刘豹,齐二石.基于多变异分析的工序控制方法研究[J].管理工程学报,2002,16(2):1-4.

[8]马义中.减小和控制多元质量特性波动的理论和方法[D].西安:西北工业大学博士论文,2002.

Identifying the Key Quality Characteristics of the Cigarette-making Enterprises Based on the Structural Equation Model

YU Hongji

(CPC School of Xuchang Committee,Xuchang 461000,China)

The production process of cigarette-making enterprises is a multistage process,which is so complex that some traditional identification methods can not result in a satisfying effect.The structural equation model can solve this problem.The model can simultaneously deal with multiple dependent variables,allow both independent and dependent variables to have measurement errors,and correct the original model based on goodness of fit index.Through a concrete example,this paper tries to analyze the key quality characteristics of the cigarette-making enterprises.

key quality characteristics; structural equation; principal component analysis

2015-12-04

于洪基(1988-)，男，河南许昌人，硕士研究生，研究方向:质量管理。

F273.1

A

1671-1181(2016)03-0031-04