一种新的等角紧框架构造方法

杨俊宾，汪立新

(杭州电子科技大学通信工程学院，浙江 杭州 310018)



一种新的等角紧框架构造方法

杨俊宾，汪立新

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

框架是一组继承了正交基的良好性质并且具有一定冗余度的线性序列，可以有效地表示信号并获得信号的重要特征.而格拉斯曼框架一直是框架理论中最重要的组成部分.针对于格拉斯曼框架的构造难题，提出了一种新的等角紧框架构造方法.方法基于区组设计和斯坦纳系统的联合.可构造出较高维度的等角紧框架，拓宽了格拉斯曼框架构造的范围，为格拉斯曼框架的构造提供了新的思路.

框架理论；格拉斯曼框架；等角紧框架；斯坦纳系统

0　引　言

在CDMA通信系统中，每个用户通过不同的码序列来区分用户之间的信息.最优格拉斯曼框架(Grassmannian Frame, GF)或者等角紧框架(Equal Tight Frame, ETF)是冗余度相同的所有框架中，元素之间的最大互相关最小的框架[1].由于等角紧框架具有优异的互相关性能，因此，可以用它来构建通信系统中的扩频码序列.这样的序列被称为最优格拉斯曼序列[2-4].然而，格拉斯曼框架的构造非常困难，现有的几种构造方法都有它的局限性，比如：Conference矩阵只能构造出N=2m的等角紧框架[5]；交替投影算法和遗传算法(Genetic Algorithm，GA)只能构造较低维度的等角紧框架[6-9].本文首先介绍了框架以及格拉斯曼框架的相关概念.紧接着，提出了基于区组设计(block design)和斯坦纳系统(Steiner System)等角紧框架的构造新方法.

1　框架及格拉斯曼框架的概念

框架理论是继小波分析之后发展起来的一个新研究方向，在信号处理、图像压缩、数据压缩、抽样理论、雷达及通信等方面均具有十分广阔的应用前景.1952年，R.J. DUFFIN和A.G. SCHAEFFER在研究非调和傅里叶分析时，进一步提炼了D.GABOR的方法，定义了Hilbert空间中框架的概念[10].设{fk}k∈I(I是一个有限数集合{1,2,…,N})为Hilbert空间H的一组函数序列，如果存在常数A和B对任意的f∈H，满足不等式：

(1)

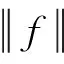
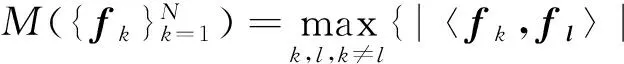
(2)

框架与正交基的不同之处在于框架是一组冗余的序列集，即框架元素的个数N大于框架元素的长度m.框架冗余度定义为ρ=N/m，而格拉斯曼框架是具有相同冗余度的所有框架中，框架元素之间最大互相关最小的框架.

2　斯坦纳等角紧框架

在提出新的等角紧框架构造方法之前，首先明确有关区组设计(blockdesign)和斯坦纳系统(SteinerSystem)的基本概念[12].对于一个(v,b,r,k,λ)设计也称为区组设计，其实质是一个数学模型.它是从v个元素中取出k个元素作为一个区组，一共可以组成b个这样的区组集合，并且这些区组集合中的元素都满足以下两个条件：

1)v中的每一个元素恰好存在于r个区组中；

2)v中的每一对元素恰好存在于λ个区组中.

在一个(v,b,r,k,λ)区组设计中，v个不同的元素每个出现r次，所以一共出现vr次.另一方面，b个不同的区组中每一个都有k个元素出现，所以一共出现bk次.得到：

vr=bk.

(3)

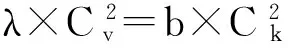
(4)

由式(3)和式(4)联立得出：

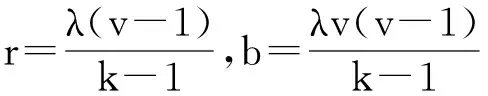
(5)

区组设计所对应的关联矩阵A是一个v×b维的矩阵，横坐标v对应元素，纵坐标b对应区组.如果元素出现在相应的区组中，则对应矩阵元素输入为1，否则为0.为了方便本文研究，将使用b×v维的关联矩阵AT.而(2,k,v)-斯坦纳系统表示，V中任意一对元素只出现在一个区组中，即λ=1.因此，(2,k,v)-斯坦纳系统为：

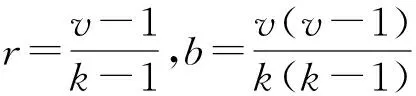
(6)

对应的{0,1}-关联矩阵AT的构造方法如下：

2)AT的每一行有k个1；

4)AT的任意两列的内积为1.

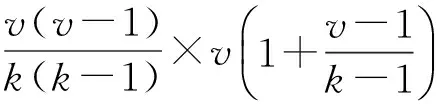
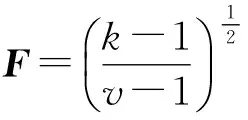
证明上述矩阵F是等角紧框架.

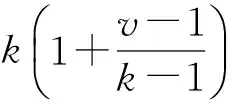
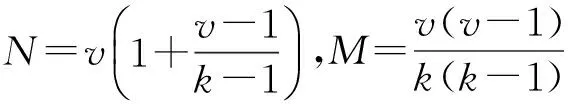
为了更好地理解上述构造等角紧框架的过程，下来给出一个简单的实例，构造一个基于(2,2,4)-斯坦纳系统的等角紧框架.

由(2,2,4)-斯坦纳系统可以看出k=2，v=4.因此，事件矩阵AT是一个6×4维的矩阵，并且每一行有2个1，每一列有3个1，任意两列的内积为1.由此得到的关联矩阵

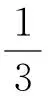
3　结束语

在扩频通信系统中，用最优格拉斯曼框架组建扩频码序列，不仅可以降低用户之间的相互干扰，而且在接收端可以有效地恢复出原始数据.但是格拉斯曼框架的构造是一个十分困难的问题，尤其是高维数格拉斯曼框架的构造更加困难.本文提出了一种新的格拉斯曼框架构造方法，可以有效地构造出高维数格拉斯曼框架，为格拉斯曼框架的构造提供了新的思路.在实际CDMA扩频码本的组建应用中有着十分重要的价值.

[1]STROHMER T,HEATH R W.Grassmannian frames with applications to coding and communication [J].Applied & Computational Harmonic Analysis,2003,14(3):257-275.

[2]HEATH R W,STROHMER T,PAULRAJ A J.Grassmannian signatures for CDMA systems[C]//Global Telecommunica

tions Conference,2003.GLOBECOM′03.IEEE.IEEE,2003:1553-1557.

[3]HEATH R W,STROHMER T,PAULRAJ A J.On quasi-orthogonal signatures for CDMA systems[J].Information Theory,IEEE Transactions on,2006,52(3):1217-1226.

[4]VANHAVERBEKE F,MOENECLAEY M.Binary signature sets for increased user capacity on the downlink of CDMA systems[J].Wireless Communications,IEEE Transactions on,2006,5(7):1795-1804.

[5]STROHMER T.A note on equiangular tight frames[J].Linear Algebra and its Applications,2008,429(1):326-330.

[6]TROPP J,DHILLON I S,HEATH R W,et al.Designing structured tight frames via an alternating projection method[J].Information Theory,IEEE Transactions on,2005,51(1):188-209.

[7]HEATH R W,TTOPP J A,DHILLON I S,et al.Construction of equiangular signatures for synchronous CDMA systems[C]//Spread Spectrum Techniques and Applications,2004 IEEE Eighth International Symposium on.IEEE,2004:708-712.

[8]ISAACS J C,ROBERTS R.Constructions of equiangular tight frames with genetic algorithms[C]//Systems,Man and Cybernetics,2009.SMC 2009.IEEE International Conference on.San Antonio:IEEE,2009:595-598.

[9]ISAACS J C.Stochastic constructions of equiangular tight frames[C]//Digital Signal Processing Workshop and IEEE Signal Processing Education Workshop (DSP/SPE),2011 IEEE.Sedona,AZ:IEEE,2011:66-71.

[10]曲长文,何有,刘卫华,等.框架理论及应用[M].北京:国防工业出版社,2009:116-175.

[11]SARWATE D V.Meeting the Welch bound with equality[M]//Sequences and their Applications. London:Springer,1999:79-102.

[12]FICKUS M, MIXON D G,TREMAIN J C.Steiner equiangular tight frames[J].Linear Algebra and its Applications,2012,436(5):1014-1027.

A New Construction Method of Equiangular Tight Frame

YANG Junbin, WANG Lixin

(SchoolofCommunicationEngineering,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

The frame is a linear redundancy sequence which inherits the good properties of orthogonal basis. The frame can express signals efficiently and get the key characters. And the Grassmannian frame is the most important part in frame theory. The paper aims at the difficulties in constructing Grassmannian frames and proposes a new method in constructing equiangular tight frame(ETF). The new construction method is based on block design and Steiner system. It can construct high dimensionality ETF frames, expand the limits of Grassmannian frames construction, and provide new ideas for the construction methods.

frame theory; Grassmannian frame; equal tight frame; Steiner system

10.13954/j.cnki.hdu.2016.01.008

2015-06-02

杨俊宾(1989-)，男，安徽阜阳人，硕士研究生，信号与信息处理.通信作者：汪立新研究员，E-mail：hh02188171@126.com.

O151.21

A

1001-9146(2016)01-0037-04