基于理由的偏好防策略投票方案

李　娜，袁旭亮

(南开大学 哲学院，天津　300350)



基于理由的偏好防策略投票方案

李娜，袁旭亮

(南开大学 哲学院，天津300350)

所谓的社会选择理论就是将社会中众多的个体偏好聚合为社会偏好，并在此基础上做出充分体现每一社会成员的真实偏好的社会选择。20世纪70年代，吉伯特和萨特思维特提出并证明了任何合理的防策略投票方案都是独裁的，这是社会选择理论的一个非常重要的结论。为了深化对社会选择理论的认识，基于理由的偏好作为基本的偏好关系，研究不同情形下的基于理由的偏好聚合问题，构建一个基于理由的偏好投票方案，并对其防策略性进行了研究。

社会选择理论；吉伯特-萨特思维特防策略投票不可能性定理；防策略投票方案；基于理由的偏好

一、引言

所谓的社会选择理论是将社会中众多的个体偏好聚合为相应的社会偏好，进而做出一个体现每一个体的真实偏好和意愿的最佳社会选择。在形式上，社会选择理论是典型的群体决策问题，但是在更深层次上，社会选择理论所研究的是“个人价值与社会选择之间的冲突与一致性的条件”，也即协调社会成员间有分歧的价值观和不同的利害关系，使之趋于一致。对社会选择理论的研究具有悠久的历史，可以追溯到中世纪关于投票方法的研究。从18世纪开始，对社会选择问题的研究逐渐系统化，法国数学家孔多塞首先发现了“投票悖论”；数学家博达针对“少数服从多数”投票方案存在的缺陷提出了博达计数法；到20世纪50年代，美国经济学家肯尼斯·约瑟夫·阿罗提出并证明了著名的阿罗不可能性定理(简称为阿罗定理)[1]；进而，在阿罗定理的基础上，艾伦·吉伯特和马克·萨特思维特对社会选择理论进一步研究发现任何合理的投票选举方案都可以被操纵，也即吉伯特-萨特思维特防策略投票不可能性定理[2-3]。后世对社会选择问题的研究都以阿罗定理和吉伯特-萨特思维特定理为基础，试图通过弱化阿罗关于投票方案的性质条件来得到可能性定理，进而构造一种防策略(操纵)的偏好聚合机制(投票方案)[4]。

社会选择理论问题的本质是偏好的聚合问题，其关键在于构造一个完美的(防策略的)偏好聚合机制。本文以丹尼尔·欧歇尔森和斯科特·温斯坦定义的基于理由的偏好作为基本的偏好关系[5-6]，研究基于理由的偏好聚合问题，并尝试构造一个基于理由的偏好投票方案，进而对其是否具有防策略性进行研究。

二、基于理由的偏好聚合

给定名册(L,U)，令P∈L是一元谓词并且χ∈U为一个理由集。为了更清楚地阐述相关概念，将偏好关系下标处的χ省略。

定义1

φ=def∀xy((Px≈Py)→∀z((Px∧Pz)≈(Py∧Pz)))。

在定义1中，φ表示对于任意的个体x和y，若x具有性质P与y具有性质P是无差异的，那么对于任意的个体z，x具有性质P并且z具有性质P与y具有性质P并且z具有性质P也是无差异的。即：若Px与Py是无差异的，那么分别在Px与Py上合取任意的Pz其结果也是无差异的。

命题1令M=〈D,W,t,u,s〉是一个模型，w0∈φ[M]。那么存在一个实数R上的函数F：R2→R使得对于所有满足条件

(Px∧Py)[M,d]≠∅

的指派d，都有

u(s(w0,(Px∧Py)[M,d]))=F(u(s(w0,Px[M,d])),u(s(w0,Py[M,d])))。

证明：对于具有形式u(s(w0,Px[M,d]))和u(s(w0,Py[M,d]))的数，定义

(1)F(u(s(w0,Px[M,d])),u(s(w0,Py[M,d])))=defu(s(w0,(Px∧Py)[M,d]))。

对于所有其他的实数r1和r2，F(r1,r2)可以被定义为R中的任意一个元素。下面证明F是一个函数。为了这个目的，令变元q是已知的，并且假设

(2)u(s(w0,Px[M,d]))=u(s(w0,Pq[M,d]))。

为了完成这个证明，现在只需证明

(3)u(s(w0,(Px∧Py)[M,d]))=u(s(w0,(Pq∧Py)[M,d]))。

F的第二个断言可以用同样的方法处理。从式(2)可得

w0∈(Px≈Pq)[M,d],

因此，由定义1可得

w0∈((Px∧Py)≈(Pq∧Py))[M,d],

由此可得

u(s(w0,(Px∧Py)[M,d]))=u(s(w0,(Pq∧Py)[M,d]))。■

命题1说明对于由简单合取支Px和Py构成的公式Px∧Py，可以构造出一个函数F，将各个合取支的效用聚合为合取式Px∧Py的整体效用。下面是定义1的推广。

定义2

φ=def∀xy((Px≈Py)→∀x1…xk((Px∧Px1∧…∧Pxk)≈(Py∧Px1∧…∧Pxk))。

命题2令M=〈D,W,t,u,s〉是一个模型，w0∈φ[M]。那么存在一个实数R上的函数F：Rk→R使得对于所有满足条件

(Px∧Px1∧…∧Pxk)[M,d]≠∅

的指派d，都有

u(s(w0,(Px∧Px1∧…∧Pxk)[M,d]))=F(u(s(w0,Px[M,d])),u(s(w0,Px1[M,d])),…,u(s(w0,Pxk[M,d])))。

证明：利用命题1施归纳于个体的个数k即可证明。

下面笔者将讨论另一种简单的偏好聚合，也即如何将由单个理由i∈χ所索引的个体效用ui聚合为理由集χ下的复合效用uχ。令{1},{2},{1,2}∈U，并且{1}和{2}分别简写做1和2，{1,2} 简写做1,2。

定义3

φ=def∀xy(((Px≈1Py)∧(Px≈2Py))→(Px≈1,2Py))。

定义3表明，给定理由{1}和{2}，对于任意的个体x和y，若在理由1下x具有性质P与y具有性质P是无差异的，并且在理由2下x具有性质P与y具有性质P同样是无差异的，那么在理由集{1,2}下x具有性质P与y具有性质P是无差异的。

命题3令M=〈D,W,t,u,s〉是一个模型，w0∈φ[M]。那么存在一个实数集R上的函数F：R2→R使得对于所有指派d，都有

u1,2(s(w0,Px[M,d]))=F(u1(s(w0,Px[M,d])),u2(s(w0,Px[M,d])))。

证明：若存在指派d使得有序对(p,q)∈R2满足

(4)p=u1(s(w0,Px[M,d]))

q=u2(s(w0,Px[M,d]))

则称有序对(p,q)是关键的。

对任意的关键有序对(p,q)，令F：R2→R满足

F(p,q)=u1,2(s(w0,Px[M,d]))。

而对于非关键的有序对，F在其上的对应是任意的。假定对于某一指派d′，有

(5)p=u1(s(w0,Px[M,d′]))

q=u2(s(w0,Px[M,d′]))

若要证明F是一个函数，则需先证得如下式子成立

(6)u1,2(s(w0,Px[M,d]))=u1,2(s(w0,Px[M,d′]))。

令y是一个不同于x的变元，并且令

d″(z)=d(d′(x)/y)(z)。

从(4)和(5)可以推出

w0∈(Px≈1Py)[M,d″]并且w0∈(Px≈2Py)[M,d″]。

由定义3可得

w0∈(Px≈1,2Py)[M,d″]。

因此，立刻得(6)。故，F:R2→R是一个函数。■

命题3给出的R2上的一个函数F，将理由{1}和{2}分别索引的效用聚合为理由集{1,2}索引的复合效用。下面是定义3的推广。

定义4

φ=def∀xy(((Px≈1Py)∧(Px≈2Py)∧…(Px≈kPy))→(Px≈1,2,…,kPy))。

命题4令M=〈D,W,t,u,s〉是一个模型，w0∈φ[M]，效用索引{1},{2},…,{k},{1,2,…,k}。那么存在一个实数集R上的函数F:Rk→R，使得对于所有的指派d，都有

u1,2,…,k(s(w0,Px[M,d]))=F(u1(s(w0,Px[M,d])),u2(s(w0,Px[M,d])),…,uk(s(w0,Px[M,d])))。

证明：利用命题3施归纳于个体的个数k即可证明。

三、基于理由的偏好投票方案及其防策略性研究

1.吉伯特-萨特思维特防策略投票不可能性定理

20世纪70年代，吉伯特指出“任何一个至少包含三个候选项的简单博弈结构都是独裁的”，并对这一定理进行了证明[2]。萨特思维特进而提出并证明了下面的吉伯特-萨特思维特定理：

“吉伯特-萨特思维特定理在一个具有〈In,Sm,vnm,Tp〉结构的选举委员会中，其中n≥1,m≥p≥3。投票方案vnm是防策略的当且仅当它是独裁的。”[3]

吉伯特-萨特思维特定理指出任何防策略的投票方案都是独裁的，这一理论引起了计算机科学、数学、经济学和逻辑学等领域的学者的注意，吉伯特和萨特思维特的研究开启了对投票方案的防策略研究。关于吉伯特-萨特思维特定理有多种证明方法，如萨特思维特的证明方法[3]，及S.Barbera和B.Peleg的证明方法等[7]。

下面，笔者以量化偏好逻辑为理论背景，尝试为基于理由的偏好构造一个偏好聚合机制(投票方案)，随后对它的防策略性进行研究。

2.基于理由的偏好的投票方案及其防策略性研究

给定名册(L,U)，模型M=〈D,W,t,u,s〉和指派d。χ={1,2,3,…,k}∈U为理由集。令A={φ,ψ,θ,…}为候选项集，集合A的基数κ≥3，且A⊆L(L,U)。命题φ[M,d],ψ[M,d],θ[M,d],…的定义如通常，在此不赘述。命题φ[M,d],ψ[M,d],θ[M,d],…分别表示候选项φ,ψ,θ,…在其中可以实现的可能世界集。即若w′∈φ[M,d]，表示候选项φ在可能世界w′中可实现。

以下几点需作出特别解释：

在模型M=〈D,W,t,u,s〉中，

(1)选择函数s:W×W→W，因而s(w,φ[M,d])∈W。在本部分的理论背景下，选择函数s依据可能世界w从所有候选项φ可实现的可能世界中选择一个可能世界w′作为φ的代表。故而可得到候选项集A={φ,ψ,θ,…}在其中可实现的可能世界代表集A′={w′,w″,w‴,…}。

(2)效用函数u:W×U→R，因而ui(s(w,φ[M,d]))∈R，也即根据某一理由i所确定的效用规模，效用函数ui为每一个由选择函数s选出的候选项φ的可能世界代表w′指派一个效用值ui(w′)。

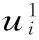
定义5(投票方案)

投票方案是一个函数f: u→W。f的值域记作rf。即投票方案f为任意的理由集χ所确定的效用截面u指派一个可能世界w′，可能世界w′也即是理由集χ下的最佳群体选择。由上文中(1)可知，w′是候选项φ的可能世界代表，故而φ即为理由集χ下的最佳群体选择。

定义6(全体一致)

投票方案f是全体一致的，如果在理由集χ下，若对于∀i∈χ，∀w∈A′，w在ui下的效用值都是最大的，则f(u)=w。

定义7(独裁)

在投票方案f中，给定理由集χ，如果对于χ下的效用截面u以及任意的w∈A′，都有ui(f(u))≥ui(w)，则i∈χ是一个独裁者。

注意，在定义7以及下文中，若j∈χ，则uj是效用截面u的第j个元素。由定义7可知，若f(u)=w*，则有对于∀w∈A′都有ui(w*)≥ui(w)。又由于ui∈u，因而在理由集χ做出的群体选择是由理由i所决定的，故i为一个独裁者。

定义8(操纵)

定理1任何至少包含3个候选项的防策略投票方案都是独裁的。

证明：这一定理的证明通过对理由的个数进行归纳而证明。

步骤一：首先证明当只有两个理由时，定理成立。令χ={1,2}，且令投票方案f是一个理由集χ下的防策略投票方案。进而只需证明f(u)所选择的候选项要么是在理由1下效用值最大的候选项，要么是在理由2下效用值最大的候选项，即理由1或理由2支配投票方案。

命题5给定任意的理由集χ={1,2}，理由集χ下的效用截面u=(u1,u2)，则f(u)要么是在理由1下效用值最大的候选项，要么是在理由2下效用值最大的候选项。

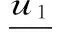
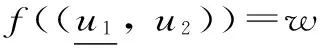
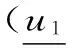
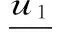
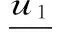
步骤1得证。

步骤2：令χ={1,2,3,…,n}，n≥3，证明(a)蕴涵(b)：

(a) 对于任意的χ′,χ′⊆χ，且χ和χ′所对应的效用截面分别是 u和u′，则如果投票方案f: u′→W是防策略的，则f是独裁的。

(b) 如果f: u→W是防策略的，则f是独裁的。

证明：假设(a)成立。令f是防策略的投票方案f: u→W。定义一个投票方案g: u′→W，令其满足如下条件：

u′=(u1,u3,…,un)，g(u1,u3,…,un)=f(u1,u1,u3,…,un)，

也即将理由1和理由2合并，并在投票方案g中用理由1表示。很明显，投票方案f和g都满足全体一致性。接下来证明投票方案g是防策略的。首先，易知理由3～n不可能操纵投票方案g，否则它们也操纵投票方案f，而这与投票方案f是防策略的相矛盾。选取由n-1个理由确定的效用截面(u1,u3,…,un)，并令

g(u1,u3,…,un)=f(u1,u1,u3,…,un)=w1。

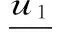
又因为投票方案f是防策略的，则

w1≠w2蕴涵u1(w1)≥u1(w2)，

w2≠w3蕴涵u1(w2)≥u1(w3)，

进而w1≠w3，蕴涵u1(w1)≥u1(w3)。因此，投票方案g不可能被理由1所操纵。

既然投票方案g满足全体一致性并是防策略的，故而根据(a)可知g是独裁的。下面有两种情形需要考虑。

情形1：假定独裁者j是理由3～n中的一个。那么理由j也是f中的独裁者。给定效用截面(u1,u2,…,un)，令w1在效用函数uj下的效用值最大，f(u1,u2,…,un)=w2。既然j支配投票方案g，则理由1在效用截面(u1,u2,…,un)下通过合并理由2而使得f(u1,u2,…,un)从w2变化为w1。因为g(u1,u3,…,un)=f(u1,u1,u3,…,un)，又因为投票方案f是防策略的，则有u1(w1)≤u1(w2)。又因为f(u1,u1,u3,…,un)=w1，则有u1(w1)≥u1(w2)，否则理由2将在(u1,u1,u3,…,un)处通过u1操纵投票方案。因而，u1(w1)=u1(w2)，则w1和w2是无差异的。因此，理由j是投票方案f的独裁者。也即投票方案f是独裁的。

则步骤二得证。

步骤三：当理由索引集χ为单元素集时，定理很明显是成立的，因而不再证明。

由数学归纳法可知，定理得证。■

四、结语

20世纪50年代，阿罗提出并证明了阿罗不可能性定理，向世界宣告“绝对公平的投票选举方案是不可能实现的”。到了20世纪70年代，吉伯特和萨特思维特在阿罗不可能性定理的基础上进一步提出了防策略投票不可能性定理，也即任何合理的投票选举方案都是可以被操纵，进一步证实了阿罗的断言。这两个定理在理论上宣告了通过投票选举获得的民主实际上是一种伪民主，其本质是一种独裁。因而不能构造出一种完美的(防策略的)投票方案，通过这一投票方案可以将社会中的众多的个体偏好聚合为一个单一的社会偏好，进而做出充分尊重每一个体的真实偏好与意愿的最佳社会选择。这是一个十分消极的结论。阿罗不可能性定理和吉伯特-萨特思维特定理的提出，促使社会选择理论成为经济学界、逻辑学界等研究的热点，后世学者试图通过弱化阿罗条件以期得到可能性定理，并对防策略投票方案进行深入的研究。本文将基于理由的偏好引入吉伯特-萨特思维特定理，尝试构造了基于理由的偏好的投票方案，并对其防策略性进行了研究，具有一定的理论创新意义和现实价值。对于基于理由的偏好的防策略投票方案的未来研究前景，笔者认为可以为基于理由的偏好的防策略投票方案构造形式语言和完全的公理系统，通过公理化的方法证明其是否具有防策略性，从而使得基于理由的偏好的防策略投票方案更加成熟和完善。

[1]肯尼斯·约瑟夫·阿罗.社会选择：个性与多准则[M].钱晓敏，孟岳良,译.北京：首都经济贸易大学出版社，2000.

[2]GIBBARD A.Manipulation of voting schemes:A general result[M].[S.l.]:Econometrica,1973:587-601.

[3]SATTERTHWAITE M A.Strategy-proofness and Arrow’s conditions:Existence and correspondence theorems for voting procedures and social welfare functions[J].Journal of economic theory,1975,10(2):187-217.

[4]罗云峰，肖人彬.社会选择的理论与进展[M].北京：科学出版社，2003.

[5]OSHERSON D,WEINSTEIN S.Preference based on reasons[J].The Review of Symbolic Logic,2011,5(1):122-147.

[6]OSHERSON D,WEINSTEIN S.Modal logic for preference based on reasons[M]//Search of Elegance in the Theory and Practice of Computation.[S.l.]:Springer Berlin Heidelberg,2013:516-541.

[7]BARBERA S,PELEG B.Strategy-proof voting schemes with continuous preferences[J].Social choice and welfare,1990,7(1):31-38.

[8]SEN A.Another direct proof of the Gibbard-Satterthwaite theorem[J].Economics Letters,2001,70(3):381-385.

(责任编辑张佑法)

The Strategy-Proof Voting Scheme of Reason-Based Preference

LI Na, YUAN Xu-liang

(School of Philosophy, NanKai University, Tianjin 300350, China)

The so-called social choice theory is a preference aggregation scheme which aggregates the numerous individual p

into a social preference and on the basis of that makes a social choice which reflects the true preference of each individual. In 1970s, the Gibbard-Satterthwaite strategy-proof voting impossibility theorem further confirms the result that every non-trivial strategy-proof voting scheme is dictatorial. In order to deepen the understanding to the social choice theory, we take reason-based preference as the basic preference relation, and first construct an aggregate function of reason-based preference, then establish a voting scheme of reason-based preference and study its strategy-proofness.

social choice theory; Gibbard-Satterthwaite strategy-proof voting impossibility Theorem; strategy-proof voting scheme; reason-based preference

2016-02-10

李娜(1958—)，女，河南开封人，教授，博士生导师，研究方向：现代逻辑。

引用格式：李娜，袁旭亮.基于理由的偏好防策略投票方案[J].重庆理工大学学报(社会科学)，2016(8):12-17.

format：LI Na, YUAN Xu-liang.The Strategy-Proof Voting Scheme of Reason-Based Preference[J].Journal of Chongqing University of Technology(Social Science)，2016(8):12-17.

10.3969/j.issn.1674-8425(s).2016.08.003

B81

A

1674-8425(2016)08-0012-06