变系数模型中稳健估计方法的比较和应用*

复旦大学公共卫生学院生物统计学教研室和公共卫生安全教育部重点实验室(200032)

黄绿斓　赵耐青　秦国友△



·论著·

变系数模型中稳健估计方法的比较和应用*

复旦大学公共卫生学院生物统计学教研室和公共卫生安全教育部重点实验室(200032)

黄绿斓赵耐青秦国友△

【提要】目的在变系数模型中比较七种常见的稳健估计方法与最小二乘法的表现，为变系数模型中估计方法的选择提供依据。方法通过R软件随机模拟，以变系数模型产生数据并对其进行污染，比较稳健估计方法和最小二乘法估计结果的偏差、方差、均方误差以及积分均方误差的差异。结果当数据存在扰动时，尤其是存在X方向上的异常点时，M-Huber、最小绝对离差(least absolute deviation,LAD)估计、MM以及R这几种稳健方法的四项指标几乎都小于最小二乘法，其中，MM表现最好。而最小截断平方法(least trimmed squares,LTS)、最小中位数平方法(least median of squares,LMS)以及S由于在R软件中稳定性较差，并不适用于变系数模型。结论在变系数模型中，当有异常点存在时，采用MM估计能得到更加准确的结果。

变系数模型稳健异常点

通常，我们使用一般线性模型来研究变量之间的关系。比如，为比较A药和B药在疗程为6个月中持续减肥的疗效，我们将10个女性肥胖志愿者随机分成2组(group=0为A药组，group=1为B药组)，分别考察这2组肥胖者在服药前、服药后3个月和6个月的体重变化(分别对应t=0,1,2)。一般线性模型可表示为：

Δt=β0+β1t+β2group+ε

(1)

其中Δt表示个体在t时刻体重增量，即Δt=Yt-Y0。β2表示时间固定时，group变化一个单位，Δt平均变化β2个单位。

考虑到药物的效果可能受时间影响，模型引入交互项：

Δt=β0+β1t+β2group+β3group·t+ε

(2)

此时，group的效应为β2+β3t，对应t=0,1,2。即时间固定时，group变化一个单位，Δt平均变化β2+β3t个单位。所以，药物的效应是关于时间的函数，随时间线性变化。推广到更一般的情况，模型可变为

Δt=g0(t)+group·g1(t)+ε

(3)

其中g0(t)，g1(t)为光滑函数，分别对应公式(2)中的(β0+β1t)和(β2+β3t)。g1(t)表示固定基线Y0和时间t，group变化一个单位，Δt平均变化g1(t)个单位，g0(t)的解释也类似。此模型实际上是变系数模型(varyingcoefficientmodel,VCM)[1]的特殊形式，不仅包含了上述所有的模型，而且更灵活、更容易解释。而变系数模型更一般的形式为

Y=g0(r0)+X1g1(r1)+…+Xpgp(rp)+ε

(4)

其中Y为响应变量，X1,X2,…,Xp以及r1,r2,…,rp均为协变量，gj(rj)(j=1,2…p)是未知的光滑函数，ε是随机误差且E(ε)=0,var(ε)=σ2。其中gj(rj)表示固定其他因素时Xj变化一个单位，Y平均变化gj(rj)个单位，这个平均变化量随rj而发生改变。变系数模型是经典线性模型的推广，具有适应性和解释性强的特点，在经济金融、流行病学、环境科学以及生物医学等领域也有着广泛应用[2-6]。

变系数模型中系数函数的估计通常可以采用基于核的局部多项式估计以及样条等方法[5]。目前，这些方法主要是建立在最小二乘法(ordinary least square,OLS)之上的，但是OLS方法对数据中异常点非常敏感，可能导致估计结果产生偏差，甚至得到完全错误的结论[5]。因此，很多学者[7-11]提出了稳健估计方法，这些方法对异常点有一定的抵抗能力。在线性模型下，稳健估计方法的比较研究很多[12-14]，但是，在较线性模型复杂的变系数模型中稳健估计方法研究并不多见。本文通过随机模拟的方法比较在各种数据污染情况下变系数模型中几种常见的稳健方法与OLS的表现，为今后变系数模型中估计方法的选择提供依据。

方　　法

本研究在自然立方样条的基础上，使用各种估计方法得到变系数模型中系数函数的估计。

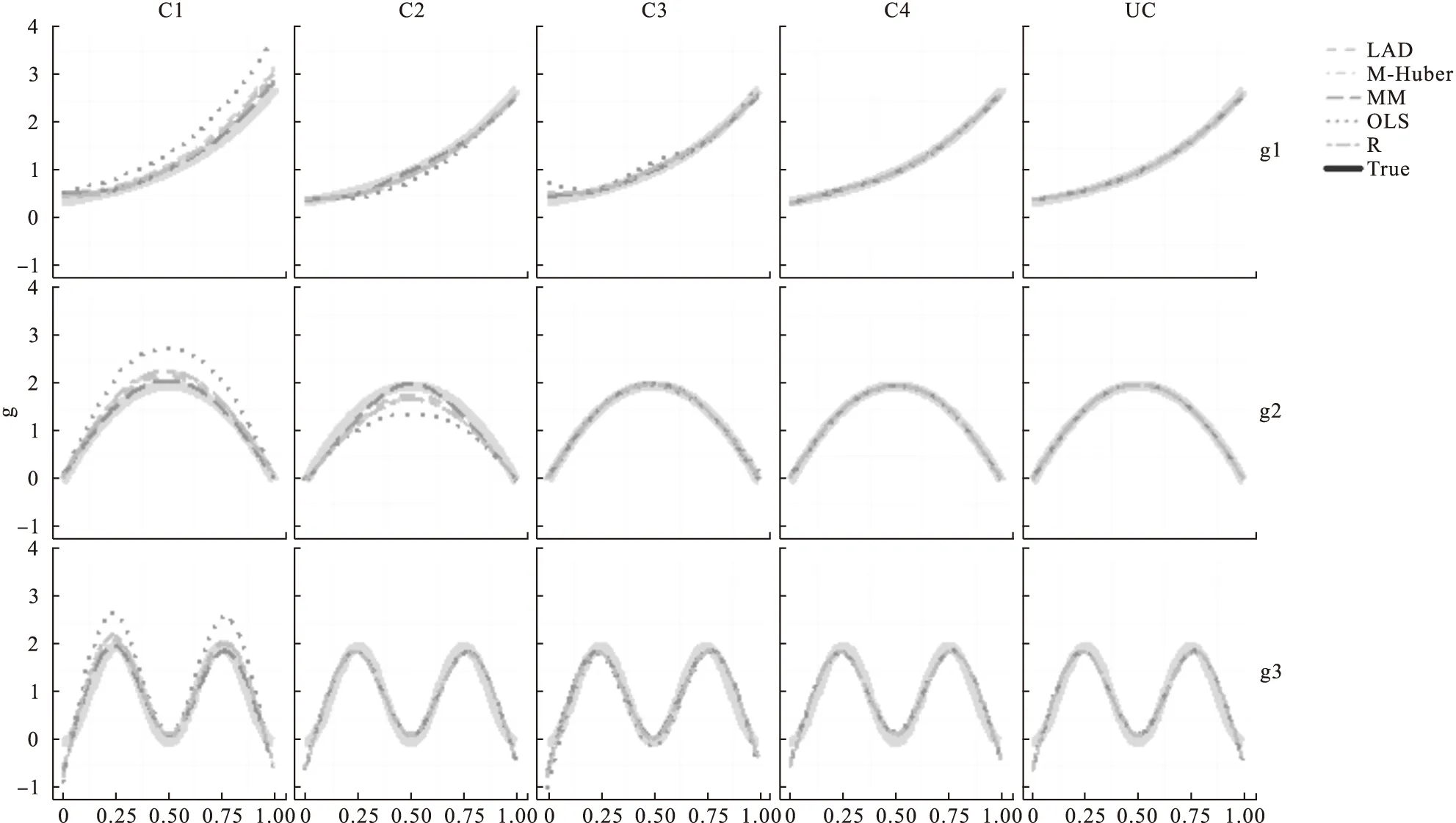
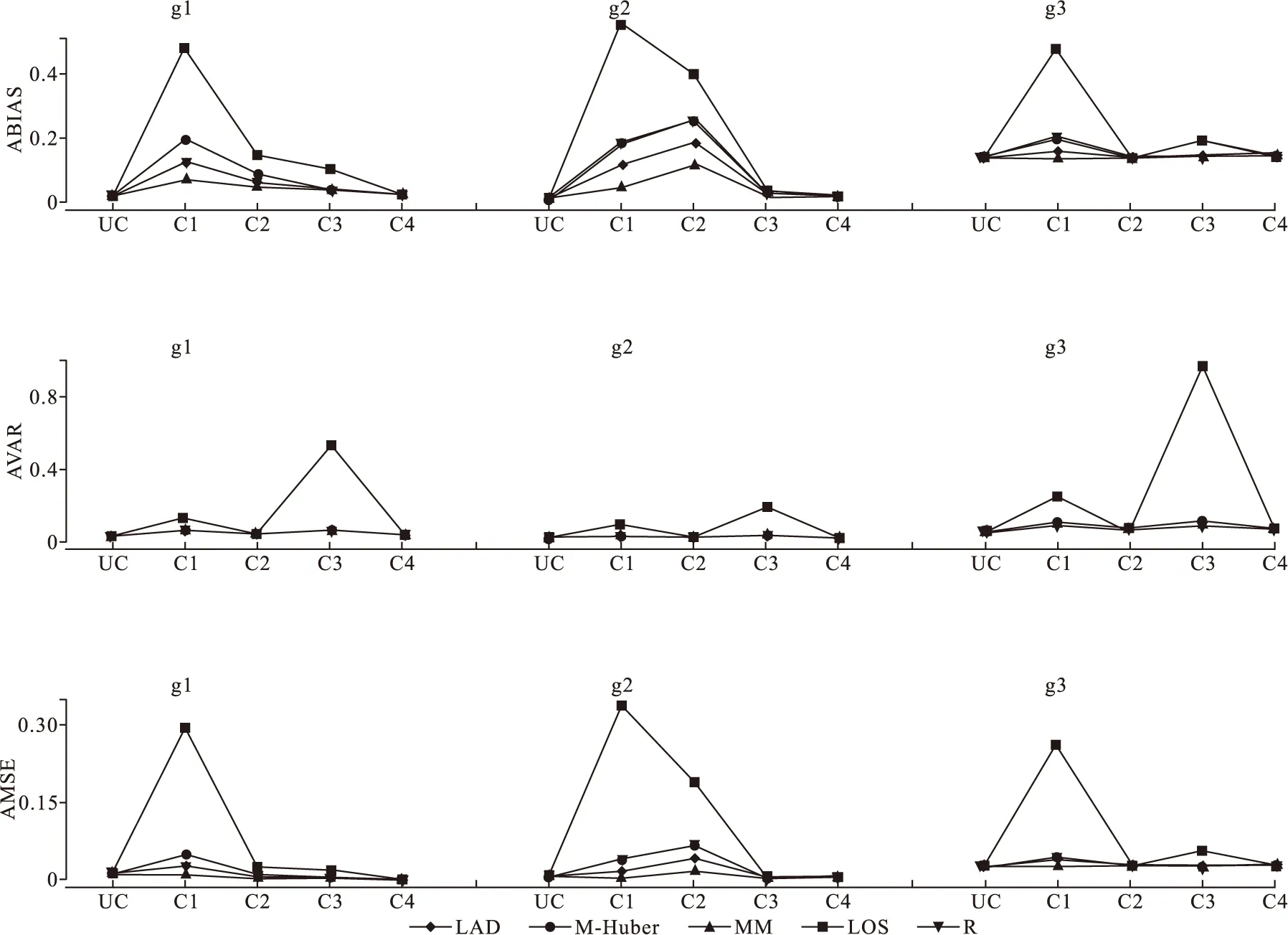
自然样条函数实际上是一分段多项式，首先对区间[a,b]进行划分:a=t1

随机模拟研究

本节将通过随机模拟比较各稳健估计在变系数模型中的表现。

我们考虑如下变系数模型[18]：

Y=g1(r)+g2(r)X1+g3(r)X2+ε

其中g1(r)=exp(2r-1),g2(r)=8r(r-1),g3(r)=2sin(2πr)2,X1～N(0,12)，X2～B[1,0.6],r～U[0,1],ε～N(0,12)，由模型产生Y，从而建立未污染数据UC。

为了研究估计的稳健性，我们通过随机选取np个点替换成其他点的方式来对原始数据进行污染，其中n表示样本量，p表示污染比例。四种污染方式分别为：C1，y方向上的污染，对随机选择响应变量Y的np个值乘以3产生异常点；C2，x方向上的污染，对随机选择协变量中连续变量X1的np个值加3来产生异常点，即均值漂移异常点；C3，误差项的污染，通过替换误差项来产生异常点，误差项服从N(0，102)并与原误差分布独立；以及C4，误差项的污染，误差项服从自由度为3的t分布。其中样本量为n=500，污染比例一般设为p=0.20，由于均值漂移异常点通常会对经典的估计产生很大的影响，C2中p设为0.05。

在以上设定的每一参数组合下，随机模拟Nsim=500次。以df=5的自然样条为基础，使用稳健方法以及OLS对变系数模型进行估计。为了衡量各方法对g(r)的估计精度，我们报告了500次模拟中积分均方误差(integrated mean square error，IMSE)[18]的均值和标准差。其中每次模拟IMSE定义如下：

此外，我们还比较了各估计的平均绝对偏差、平均方差以及平均均方误差，分别以ABIAS、AVAR、AMSE表示，并定义如下

gij(rk))2

gij(rk))2

其中i=1,…Nsim;j=1,2,3。{rk,k=1,…,ngrid}是r在[0,1]内平均分布的栅格点，ngrid=200。

结　　果

本模拟考虑了未污染数据和扰动数据，各方法500次模拟IMSE的均值和标准差结果见表1。首先，在C1～C3中MM估计表现最好，即IMSE的均值和标准差最小，其在UC和C4中表现也不错。其次，在UC中OLS的IMSE均值和标准差最小，但在扰动数据C1～C4中，有了显著的增大，尤其在C1、C2、C3中，远大于除LTS、LMS以及S估计以外的其他稳健方法的结果。最后，LTS、LMS以及S估计即使在UC中的IMSE均值和标准差也远远大于其他方法，在扰动数据中更甚，提示这三种稳健方法可能不适合变系数模型的估计。

图1表示通过稳健方法以及OLS方法，在未污染数据UC和扰动数据C1～C4中估计出的g(r)曲线。由于LTS、LMS以及S估计不稳定，远远偏离真实的曲线，图中并未画出。从中我们可以发现，在这几种方法中，真实的g(r)曲线与MM估计的曲线最接近，与OLS曲线相差最远。

表1　各方法的IMSE均值和标准差(IMSE)

*：仅取两位小数，其中每一列的最小值用粗体表示。

图1　稳健估计方法以及OLS方法估计的g(r)曲线

各估计方法的ABIAS、AVAR以及AMSE见图2，LTS、LMS以及S估计的结果由于不稳定同样并未给出。与表1的结果类似，这几种方法在UC和C4下表现良好，有较小的ABIAS、AVAR以及AMSE。在扰动数据C1～C3中，OLS的ABIAS、AVAR以及AMSE远远大于稳健方法，MM的ABIAS、AVAR以及AMSE在几乎所有的扰动情形下都明显小于或至少不大于其他方法。

图2　各稳健估计方法及OLS估计的ABIAS、AVAR以及AMSE

图3　CD4数据通过变系数模型估计的gj(t)曲线(j=0,1,2,3)

实例分析

为了研究艾滋病自然史及其影响因素，多中心艾滋病研究[19]收集了283名感染HIV病毒的男同性恋患者1984-1991年随访情况。其中t表示患者艾滋病病毒诊断后的随访观测时间(年)，Y是诊断后t时刻个体的CD4浓度，smoke表示该患者诊断前是否吸烟，age表示该患者经中心化后诊断时的年龄，preCD4表示患者诊断时中心化的CD4浓度。为研究吸烟、年龄以及基线的CD4浓度对个体CD4浓度的影响，模型可设为

Y(t)=g0(t)+g1(t)smoke+g2(t)age+g3(t)preCD4+ε

图3给出了该模型的估计结果。图(a)可表示基线浓度为42的34岁不吸烟男同性恋患者CD4浓度随时间不断下降。图(b)中吸烟的效应在0附近波动。图(c)表明年龄的效应几乎是负向的，并且近似一条斜率为-0.08的直线。表明诊断时年龄越大CD4浓度越低，时间以及其他变量固定时，年龄增加一个单位个体t时刻CD4浓度平均下降0.08个单位。图(d)表明基线CD4浓度越高，个体当前CD4浓度越高，另外，基线的影响随时间发生改变，前两年急剧减小，之后趋于平缓。另外对gj(t)是否恒等于0进行检验，除g1(t)外P值均小于0.05，表明个体t时刻CD4浓度与年龄和基线情况有关，与吸烟无关。

讨　　论

变系数模型实际上是更加一般的交互作用模型，交互作用呈非线性变化，在许多实际应用中往往被忽略，在这类模型的理论研究中往往注重理论性质而忽略了该模型具有很好的应用价值和结果的诠释，本文对模型的结果做了初步的诠释。

本文模拟研究在变系数模型中，比较了几种常见的稳健方法和OLS在处理不同类型的异常点的结果差异，发现MM估计在各情形中综合表现最好。

首先，不存在异常点时，使用自然样条的OLS、MM、Huber-M、LAD以及R估计都能较准确地得到变系数模型的估计，但LTS、LMS以及S估计效果较差。由于R中LTS、LMS以及S估计都是通过lqs函数来估计，这些方法很难得到精确的估计值并且计算量巨大。lqs函数用的是一种重抽样的近似算法[20]，由于每次都是随机抽样，所以稳定性相对较差。故而，在R软件中，LTS、LMS以及S估计不适用于变系数模型。

其次，存在Y方向上的异常点时，基于OLS估计的结果准确性以及稳定性都不及MM、Huber-M、LAD和R估计这几种稳健方法，其中MM估计效果最好。X方向的异常点对所有的估计方法都有较大的影响，尤其是对OLS方法，其结果准确性以及稳定性都不及以上几种稳健方法。误差项混合方差较大的正态分布时，对OLS影响较大。但误差项混合t分布时对结果的影响不大，增加模拟加大污染比例至0.3以及调整自由度df=4,10等也几乎没有影响。

本研究的局限在于：(1)本研究只模拟了存在一个二分类变量和一个连续型变量、两个协变量的情况，没有对多分类以及多个协变量进行模拟。(2)模型中由于没有考虑两个或以上的连续型协变量，并未考虑变量之间的相关性。(3)本研究考虑了4种类型的污染，但是实际数据往往更加复杂，一个数据中可能存在多种类型的污染。对于这些不足，我们将在以后做进一步的研究。

[1]Hastie T,Tibshirani R.Varying-coefficient Models.Journal of the Royal Statistical Society.Series B(Methodological),1993,55(4):757-796.

[2]Fan J,Zhang W.Statistical methods with varying coefficient models.Stat Interface,2008,1(1):179-195.

[3]Fan J,Zhang W.Statistical estimation in varying coefficient models.Ann Stat,1999,27(5):1491-1518.

[4]Park B,Mammen E,Lee Y,et al.Varying Coefficient Regression Models:A Review and New Developments.Int Stat Rev,2015,83(1):36-64.

[5]Feng L,Zou C,Wang Z,et al.Robust spline-based variable selection in varying coefficient model.Metrika,2015,78(1):185-118.

[6]徐丽红,刘志永,刘桂芬,等.纵向监测连续非随机缺失数据变系数模型及其应用.中国卫生统计,2012,29(3):314-317.

[7]Yohai V,Zamar R.High Breakdown-Point Estimates of Regression by Means of the Minimization of an Efficient Scale.J Am Stat Assoc,1988,83(402):406-413.

[8]Rousseeuw P.Least median of squares regression.J Am Stat Assoc,1984,79(388):871-880.

[9]Rousseeuw P,Yohai V.Robust regression by means of S-estimators.Springer,1984.

[10]Jaeckel L.Estimating Regression Coefficients by Minimizing the Dispersion of the Residuals.The Annals of Mathematical Statistics,1972,43(5):1449-1458.

[11]Huber P.Robust estimation of a location parameter.The Annals of Mathematical Statistics,1964,35(1):173-101.

[12]Alma.Comparison of Robust Regression Methods in Linear Regression.Int J Contemp Math Sciences,2011,6(9):409-421.

[13]Anderson C,Schumacker R.A comparison of five robust regression methods with ordinary least squares regression:Relative efficiency,bias,and test of the null hypothesis.Understanding Statistics:Statistical Issues in Psychology,Education,and the Social Sciences,2003,2(2):179-103.

[14]Schumacker R,Monahan M,Mount R.A comparison of OLS and robust regression using S-PLUS.Multiple Linear Regression Viewpoints,2002,28(2).

[15]丁士俊,陶本藻.自然样条非参数回归模型及模拟分析.测绘通报,2004-1-25(1):17-19.

[16]Hastie T,Tibshirani R,Friedman J.The Elements of Statistical Learning:Data Mining,Inference,and Prediction.Springer,2011.

[17]Rousseeuw P,Hubert M.Robust statistics for outlier detection.Wires Data Min Knowl,2011,1(1):73-79.

[18]Wang L,Kai B,Li R.Local Rank Inference for Varying Coefficient Models.J Am Stat Assoc,2009,104(488):1631-1645.

[19]Kaslow R,Ostrow D,Detels R,et al.The Multicenter AIDS Cohort Study:rationale,organization,and selected characteristics of the participants.Am J Epidemiol,1987,126(2):310-318.

[20]Rousseeuw P,Hubert M.Recent developments in PROGRESS.L1-Statistical Procedures and Related Topics IMS Lecture Notes,1997,3:201-214.

(责任编辑：邓妍)

Comparison of Robust Methods for Varying Coefficient Model

Huang Lvlan,Zhao Naiqing,Qin Guoyou.

(Department of Biostatistics,School of Public Health and Key Laboratory of Public Health Safety,Fudan University(200032),Shanghai)

ObjectiveTo compare the performance of several common robust methods and Ordinary Least Square(OLS)in varying coefficient model.MethodsWe used R software to simulate uncontaminated data and contaminated data.Bias,variance,mean square error(MSE)and integrated mean square error(IMSE)were used for the evaluation indices to compare the performance of these robust methods and OLS.ResultsWhen outliers were present,especially occured in x-space,M-Huber,LAD(Least Absolute Deviation),MM and R performed much better than OLS with smaller Bias,variance,MSE and IMSE in almost all cases.Among them,MM performed best overall against a comprehensive set of outlier conditions.Furthermore,LTS(Least Trimmed Squares),LMS(Least Median of Squares)and S did not seem to apply in varying coefficient model for their instability in R software.ConclusionWhen outliers occured,MM resulted in more accurate results in varying coefficient model.

Varying coefficient model;Robustness;Outlier

国家自然科学基金(11371100)

秦国友，Email:gyqin@fudan.edu.cn