环Fp+uFp上的循环码

孔　波，　常晓鹏

(1.河南教育学院 数学与统计学院　河南 郑州 450046； 2.河南教育学院 信息技术系　河南 郑州 450046)



环Fp+uFp上的循环码

孔波1，常晓鹏2

(1.河南教育学院 数学与统计学院河南 郑州 450046； 2.河南教育学院 信息技术系河南 郑州 450046)

研究了环Fp+uFp上循环码的结构, 这里p为素数,u2=u, 证明了该环上的循环码可由Fp+uFp上的一个多项式生成，并给出了其上循环码的生成多项式.

循环码; 主理想; Gray映射; 自正交码

0　引言

1　基础知识

有限交换环R上如果只有一个元素I生成，则I称为主理想. 如果环R的所有理想都是主理想, 则称R为主理想环. 如果R有唯一的极大理想R称为局部环.如果R的所有理想按包含关系形成一条链,则称R为链环.R上长为n的线性码C是Rn的一个R子模.

令R=Fp+uFp,这里u2=u. 已知Fp+uFp是特征为p的有限交换环, 该环有p2个元素.

引理1环R中有(p-1)2个单位元.

证明环R的任意元素r可以表示为r=a+bu, 由环的特征为p及u2=u, 可得rp=r. 则r(rp-1-1)=0,r∈R. 由此可得, 对任意的r∈R除了满足rp-1=1的都是零因子. 由rp-1=ap-1+u(a+b)p-1-uap-1=1. 可得ap-1=1,(a+b)p-1=1, 只要满足a≠0,a+b≠0即可.所以在R中满足a≠0,a+b≠0的有(p-1)2个元素, 可得环R中有(p-1)2个单位元.

环R是一个半局部环,R有两个极大理想

〈u〉={0,u,2u,…,(p-1)u}，〈1-u〉={0,1-u,2-2u,…,p-1-(p-1)u},

每个极大理想有p个元素, 所以R/〈u〉与R/〈1-u〉都同构与Fp，R是一个主理想环，但不是有限链环.

设σ表示Rn上的一个循环移位, 即对任意的(c0,c1,…,cn-1)∈Rn,σ(c0,c1,…,cn-1)=(cn-1,c0,…,cn-2). 设C为R上的长为n的线性码,对任意的 (c0,c1,…,cn-1)∈C, 均有σ(c0,c1,…,cn-1)=(cn-1,c0,…,cn-2)∈C, 称C为环R上长为n的循环码.

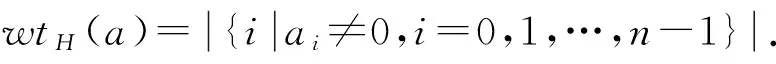
2　Gray映射

定理2若C是R上长为n的(n,k,dL)线性码. 则φ(C)是Fp上的(2n,k,dH)线性码, 且dH=dL.

证明设ri=ai+ubi∈R,i=1,2,k∈Fp. 则

φ(r1+r2)=φ(a1+a2+u(b1+b2))=(a1+a2,a1+a2+b1+b2)=(a1,a1+b1)+(a2,a2+b2)=

φ(r1)+φ(r2)φ(kr1)=φ(ka1+kub1)=(ka1,ka1+kb1)=k(a1,a1+b1)=kφ(r1)，

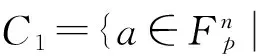
定理3设C是R上长为n的线性码. 则

这里gi为Ci的生成多项式,i=1,2.

证明对任意的(s1,s2,…,sn,t1,t2,…,tn)∈φ(C), 令ri=si(1-u)+tiu. 由φ是双射可知r=(r1,r2,…,rn)∈C. 由C1,C2的定义可知(s1,s2,…,sn)∈C1, (t1,t2,…,tn)∈C2, 所以(s1,s2,…,sn,t1,t2,…,tn)∈C1⊗C2, 即φ(C)⊆C1⊗C2.

反之, 若(s1,s2,…,sn,t1,t2,…,tn)∈C1⊗C2, 其中：(s1,s2,…,sn)∈C1； (t1,t2,…,tn)∈C2.存在x=(x1,x2,…,xn),y=(y1,y2,…,yn)∈C满足xi=si+umi,yi=ti+(1-u)ni, 其中：mi，ni∈Fp，i=1,2,…,n. 由C是线性的可知r=(1-u)x+uy∈C, 因此φ(r)=(s1,s2,…,sn,t1,t2,…,tn), 所以C1⊗C2⊆φ(C), 可得φ(C)=C1⊗C2, 由φ是双射,可知

这里gi为Ci的生成多项式,i=1,2.

引理2设C是R上长为n的线性码,C⊥为C的对偶码,则φ(C⊥)=φ(C)⊥，若C是自对偶的,则φ(C)也是自对偶的.

证明先证φ(C⊥)⊆φ(C)⊥, 设x,y∈C,其中：

x=(a1+b1u,a2+b2u,…,an+bnu)；y=(c1+d1u,c2+d2u,…,cn+dnu)；ai,bi,ci,di∈Fp.

可得

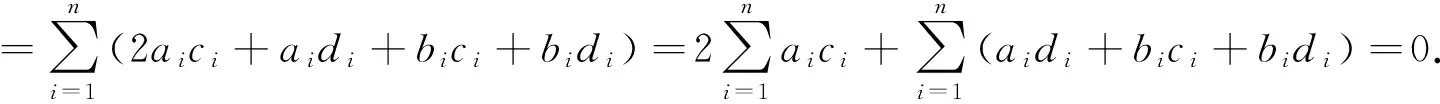
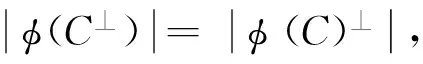
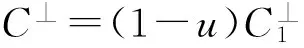
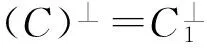
3　环R上的循环码

引理3如果C=(1-u)C1⊕(u)C2为R上的线性码, 则C为R上的循环码当且仅当C1,C2为Fp上的循环码.

证明设(x1,x2,…,xn)∈C1, (y1,y2,…,yn)∈C2, 则

((1-u)x1+uy1,(1-u)x2+uy2,…,(1-u)xn+uyn)∈C.

由C为R上的循环码可得 ((1-u)xn+uyn,(1-u)x1+uy1,…,(1-u)xn-1+uyn-1)∈C,

即

((1-u)xn+uyn,(1-u)x1+uy1,…,(1-u)xn-1+uyn-1)=

(1-u)(xn,x1,…,xn-1)+u(yn,y1,…,yn-1)∈C,

所以(xn,x1,…,xn-1)∈C1, (yn,y1,…,yn-1)∈C2,C1,C2均为Fp上的循环码.反过来, 若C1,C2均为Fp上的循环码, 设(x1,x2,…,xn)∈C1, (y1,y2,…,yn)∈C2, 则

((1-u)x1+uy1,(1-u)x2+uy2,…,(1-u)xn+uyn)∈C.

由C1,C2均为Fp上的循环码可知(xn,x1,…,xn-1)∈C1, (yn,y1,…,yn-1)∈C2, 可得

((1-u)xn+uyn,(1-u)x1+uy1,…,(1-u)xn-1+uyn-1)=

(1-u)(xn,x1,…,xn-1)+u(yn,y1,…,yn-1)∈(1-u)C1⊕(u)C2=C.

所以C为R上的循环码.

推论2如果C=(1-u)C1⊕(u)C2是R的循环码, 则C⊥也是R上的循环码.

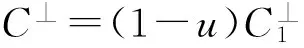
定理4如果C=(1-u)C1⊕(u)C2是R上的循环码自对偶码, 当且仅当C1,C2为Fp上的循环码自对偶码.

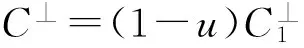
定理5如果C=(1-u)C1⊕(u)C2是R上长为n的循环码 , 则存在g(x)∈R[x]且g(x)|xn-1, 使得C=〈g(x)〉.

证明若C=(1-u)C1⊕(u)C2是R上长为n的循环码. 设gi为Ci的生成多项式,i=1,2.则

C=〈(1-u)g1(x),ug2(x)〉.

令C′=〈(1-u)g1(x)+ug2(x)〉，易得C′⊆C.由

(1-u)[(1-u)g1(x)+ug2(x)]=(1-u)g1(x),

u[(1-u)g1(x)+ug2(x)]=(u)g2(x)，

xn-1=[(1-u)g1(x)+ug2(x)][(1-u)f1(x)+uf2(x)].

所以xn-1=g(x)[(1-u)f1(x)+uf2(x)], 定理得证.

4　结论

本文根据Gray映射建立Fp+uFp(u2=u) 上的循环码与Fp上准循环码之间的对应关系,证明了环Fp+uFp上的循环码是主理想生成的.

[1]CENGELLENMIS Y. On the cyclic codes overF3+vF3[J]. International journal of algebra, 2010, 4(6): 253-259.

[2]SHI M, YANG S, ZHU S. Good p-ary quasi-cyclic codes from cyclic codes overFp+vFp[J]. Journal of systems science and complexity, 2012, 25(2): 375-384.

[3]丁健, 李红菊, 左学武, 等. 环F2+uF2+u2F2上的常循环码[J]. 电子学报, 2015,43(1):145-150.

[4]余海峰, 朱士信, 张霞. 环F2+uF2+vF2+uvF2上的1+uv-常循环码[J]. 电子与信息学报,2014, 36(6):1419-1422.

[5]周颖，李敏，魏俊潮. Abel环的一些刻画(Ⅱ) [J]. 扬州大学学报(自然科学版), 2015,18(1):1-8.

[6]CENGELLENMIS Y, DOUGHERTY S T. Cyclic codes overAk[C] // Proceedings of ACCT 2012. Pomorie, Bulgaria, 2012.

[7]LIU X S, XU X F. Cyclic and negacyclic codes of length 2psoverFpm+uFpm[J]. Acta mathematica scientia,2014, 34(3): 829-839.

[8]DERTLI A, CENGELLENMIS Y, EREN S. On quantum codes obtained from cyclic codes over A2[J]. International journal of quantum information, 2015, 13(3): 1550031.

[9]常晓鹏, 孔波, 郑喜英. 环Fpm+uFpm+…+uk-1Fpm上常循环码的等价性[J]. 郑州大学学报(理学版), 2014, 46(2): 16-20.

[10]郑喜英, 孔波, 刘洁，等. 环Fpm+uFpm+vFpm+uvFpm上长为2ps的λu-1常循环码[J]. 郑州大学学报(理学版), 2015, 47(2): 27-32.

(责任编辑：方惠敏)

Cyclic Codes over RingFp+uFp

KONG Bo1，CHANG Xiaopeng2

(1.SchoolofMathematicsandStatistics,HenanInstituteofEducation,Zhengzhou450046,China;2.DepartmentofInformationTechnology,HenanInstituteofEducation,Zhengzhou450046,China)

The structure of cyclic codes over ringFp+uFpwas studied, whereu2=u. It was proved that the cyclic codes over the ring were generated by one polynomial over the ringFp+uFp. And the generator polynomial of the cyclic codes was given.

cyclic codes; principal ideal; Gray map; self-orthogonal codes

2016-01-25

河南省基础与前沿基金资助项目(162300410083);河南教育学院应用数学重点学科资助项目.

孔波(1980—)，男，河南周口人，讲师，主要从事代数与编码研究，E-mail:kongbo666@163.com．

O157.4

A

1671-6841(2016)03-0028-04

10.13705/j.issn.1671-6841.2016017

引用本文:孔波，常晓鹏．环Fp+uFp上的循环码[J] ．郑州大学学报(理学版)，2016，48(3)：28-31．