结合形状特征点和灰度信息的心脏DSCT图像配准*

陈　昭　谢勤岚

(中南民族大学生物医学工程学院　武汉　430074)



结合形状特征点和灰度信息的心脏DSCT图像配准*

陈昭谢勤岚

(中南民族大学生物医学工程学院武汉430074)

论文引进Marching Cubes算法提取心脏腔室结构形状标记点,利用匹配原则并借助于特征向量图形成匹配的特征点对,再以此为先验知识改进互信息相似性测度函数,最终通过自适应梯度下降优化方法寻找最优的配准参数,从而实现全心脏的自动分割。实验结果表明,论文提出的方法优于基于传统的互信息配准算法。

先验知识; 互信息; Marching Cubes; 自适应梯度下降法

Class NumberTP391

1　引言

随着国家经济的迅猛发展和人民生活水平的快速提高,心血管疾病[1]的发病率和死亡率逐渐增高,严重威胁着全世界人民的健康,因此极早地对心血管疾病做出定量诊断和功能评价,起着非常重要的作用。由于双源CT(Dual-Source CT, DSCT)[2]能快速获取同一部位的组织结构形态,特别是扫描高速运转的结构如冠状动脉及腔室等,具有极高的时间分辨率,因此普遍作为心脏疾病辅助诊断的手段。

根据心脏形态评估心功能有助于提高心脏病诊断的准确性,借助于医学影像信息,从双源CT图像中提取出心脏的结构信息,并对心脏功能进行数据评估,能够实现对心血管疾病的定量诊断。研究表明基于配准的全心脏分割方法[3]是一种有效地提取心脏信息的方法,其主要思想是通过配准算法分割出心脏的各个腔室,从而能定量测度各个腔室的结构,提高诊断的正确率。

医学图像配准是通过寻找一种空间变换关系,使两幅图像中关键对应点达到空间位置和解剖结构的一致。目前医学图像的配准方法大体可以分为两类：基于特征点的图像配准和基于灰度信息的图像配准；基于灰度的方法主要利用图像像素灰度值进行图像相关性度量,计算量较大,并没有充分利用图像中一些内在的空间信息,主要有最大互信息法、互相关法和最小灰度差法等；基于特征的方法结合图像空间信息提取点、线或面的特征对集进行配准,可以充分降低配准过程中由于图像平移、旋转、缩放以及尺度原因所导致的配准难度,常见的是尺度不变特征变换(Scale Invariant Feature Transform, SIFT)[5]方法,其主要是提取整幅图像的局部特征,形成的特征点对比较分散性,不能完全表征物体的形态结构,并且有限特征点对很难估计精确的变换参数。

根据周玉新等对图像灰度信息与特征信息相结合的方法来改进配准精度的研究,本文结合最大互信息与心脏形状特征点信息[6],弥补单一采取灰度信息或图像特征进行配准的不足,以显著提高配准精度,从而准确地实现全心脏分割。文中采用Lorensen等[4]提出来的行进立方体方法(Marching Cubes, MC)自动提取心脏形状特征点,MC方法的本质是根据二值图像数据构造出等密度表面的三角面片网格模型,形状特征点即为三角网格顶点,以此形成表征心脏各个腔室边缘结构的点集,并依据现有的匹配原则形成匹配的特征点对,此时组织结构边缘的形状信息点数量较多,能够应对较复杂形变结构的图像配准。

2　配准算法

配准过程主要分成两步：第一步利用仿射变换方法以实现对心脏位置的初步定位,达到粗配准的效果；第二步采用B样条的自由形变模型方法对心脏局部结构进行非刚性变换以实现精配准。本文利用已提取的形状特征点对改进传统的互信息作为相似性测度函数应用于配准过程中,并使用自适应梯度下降法寻找最优的配准参数,最终根据基于配准方法的分割框架(如图1所示)分割全心脏各个腔室结构,其主要思想为根据浮动图像与参考图像间像素点的映射关系即最优的配准变换参数,实现图谱标记点传递,最后完成全心脏的自动分割。

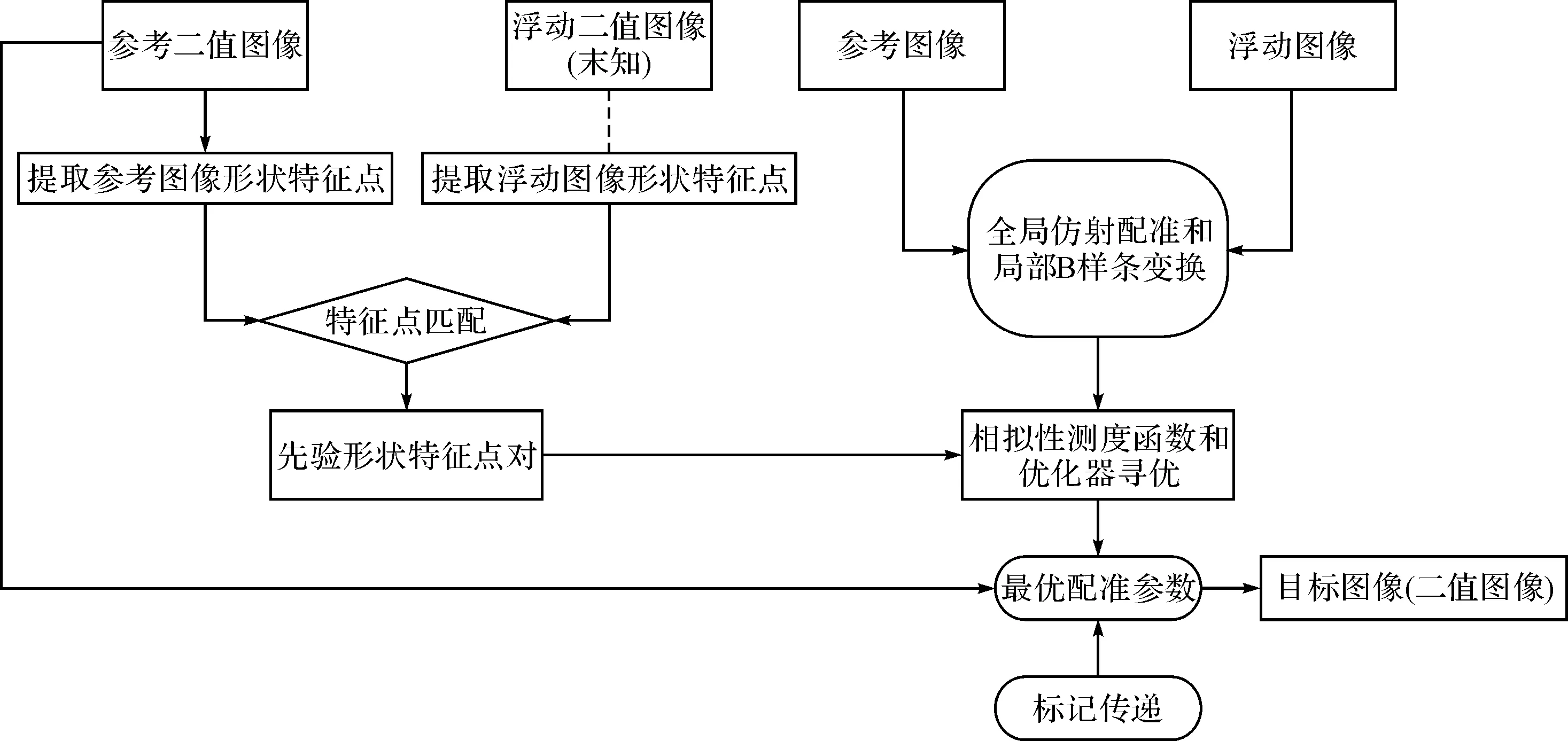
图1　基于配准方法的分割框架

2.1形状特征点提取与匹配

心脏的形状是对目标范围的二值图像表示,形状是其最基本的特征。根据临床医师专业指导手动分割心脏的各个腔室结构形成二值图像,其包含目标区域的轮廓线,然后根据轮廓线信息提取形状标记点。文中采用Marching cubes算法自动提取能够表征心脏结构的形状特征点,此特征点集包含心脏结构较多细节,手动分割的目标边缘线非常正确,因而得到的特征点能够较为正确地表达心脏结构,标记点位置严格位于目标边缘线上。经过MC算法提取的候选特征点数量庞大,还需利用Schroeder等[7]提出的三角面片消减法降低形状标记点的数量,选取特定的消减比率ρ(本文选用98%)得到一定数量的三角面片网格顶点,构成最终表征心脏结构形状的特征点集。

由于浮动图像为待分割图像,其二值图像为未知图像,因此我们并不能直接使用Marching Cubes算法提取浮动图像的形状特征点,而是利用参考图像与浮动图像互信息配准后得到的配准参数实现参考图像特征点的传递,由此得到浮动图像初步形状特征点集如图2所示。由于此特征点集并不能完全表征心脏的形状特征,故需要在该点集的每一标记点的某一邻域(文中选取12*12*12)内,利用匹配原则寻找最优的且相互匹配的特征点集。

2.1.1形状信息点特征描述符的生成

精确确定参考图像与浮动图像中标记点位置信息后,还需确定形状标记点的特征描述符,通常用特征向量表示,特征向量可以描述局部图像结构,并且能够提供大量的辅助形状信息,精确的标记点特征描述符有助于提高配准精度。本文使用L. Florack提出[10]的笛卡尔图像结构算子作为标记点的特征算子,其思想为对于每一灰度图像都含有15张描述该图像特征的辅助图像即L、gTg、gTHg、gTHHg、tr(H)、tr(HH) 和tr(HHH),其中L代表原来的灰度图像,g=(∂L/∂x) 为原图的空间偏导,H为原图的Hessian矩阵,以及tr(.) 为矩阵的迹。如果分别计算尺度为σ= 1和2时的高斯导数,可以得到15张特征图像,因此对于图像上已知位置信息的标记点其必含有15维特征向量,其中14维包含该标记点丰富的局部结构梯度信息,所有重要的结构信息对于平移和旋转有很强的鲁棒性,其中图3为部分特征向量图,图像均已归一化处理,其像素均值为0和方差为1。

图2　参考图像标记点传递

图3　特征向量图(a)原始图像　(b)平滑图像(σ= 1),(c)～(h)是局部特征图(σ= 1),其中(c)gTg、(d)gTHg、 (e)gTHHg、(f)tr(H)、 (g)tr(HH)、(h)tr(HHH)

2.1.2特征点的匹配

假如已经从两幅图像即参考图像F和浮动图像M中提取出表征组织结构形状的特征点,计算F中某一个特征点的特征向量与M中所有特征点的特征向量之间的欧式距离。若M中的两个特征点m1和m2是对应于参考图像F中的某一特征点f的最邻近点和次邻近点,则分别用d(f,m1)和d(f,m2)表示向量最邻近距离和次邻近距离,如果两者的比值小于某一阈值Tm即如下,则认为f与m1相匹配。

(1)

2.2结合形状特征点和互信息的配准

配准质量的优劣很大程度上依赖于相似性测度目标函数的选择,配准过程实则是根据相似性测度函数并以某种寻优算法进行最佳选择,得到最理想的配准参数的过程。本文采用基于特征点信息与基于灰度信息相结合的方法,将负互信息与点约束项的和表示为相似性测度函数如式(2),以提高配准速度与配准精度。

C=-CMI+ωCp

(2)

其中第一项CMI为MI,第二项Cp为表征心脏结构形状信息的特征点约束项,而权重因子ω(0.01<ω<0.1)用来权衡两项的贡献程度。

假设已经提取出参考图像If与浮动图像Im中N个表征心脏形状结构的特征点对为{(pfi,pmi);i=1,2,…,n},其中pfi={xfi,yfi,zfi}和pmi={xmi,ymi,zmi}分别是位于参考图像与浮动图像中的特征点,则将其表示为相似性测度函数的约束项Cp,并定义为

(3)

其中Tμ(·)为变换函数,‖·‖为欧式距离。

本文采用Klein提出[9]的自适应梯度下降法(Adapted-Self Gradient Descent, ASGD)寻找最佳的变换参数,以使相似性测度函数最小化,其中约束项Cp相对于变换参数μ的梯度函数为

(4)

参数寻优实则是使心脏图像灰度信息与心脏结构形状信息相互折中的过程,从而减少单一的互信息配准因未考虑心脏结构空间信息而导致误配准的情况,确切的形状特征点更能提高配准的精度,从而准确地实现心脏分割。

3　实验结果与分析

本文使用的是由广州军区广州总医院的DSCT扫描系统上采集的图像数据,并且在Visual Studio 2012开发环境下利用C++编程实现基于ITK[8]的配准算法,将程序运行于CPU Intel Dual-Core 3.2GHz, RAM 32G的PC机上,利用Elastix医学图像配准工具包进行实验。

3.1配准实验结果

为了验证本文改进算法的优势,本文进行两组实验,第一组实验使用传统基于互信息的配准方法,作为对照组,第二组实验使用本文提出的基于形状特征点结合互信息的配准方法,作为实验组。两组实验都选取5个不同的病人其10个时相作为参考图像,并且选取由5个不同病人10个不同时相所制作的平均模板图像作为浮动图像。图5为两组配准实验的效果图,其中(a)和(b)分别是参考图像与浮动图像,(c)和(d)分别为互信息配准结果和本文方法配准结果。为了便于比较,图中所选的心脏图像是同一病人同一时相同一层面的断层图像,从图中可以看出,本文提出的改进算法能得到更为精确的配准结果,结构边缘清晰,呈现较少误配准区域如图中箭头所示。

图4　基于本文方法与基于传统MI方法配准结果比较

3.2分割实验结果

如图6所示为本文提出方法与基于传统MI配准分割方法在不同断层的结果对比图,由图可见,本文方法能够得到更为精确的分割轮廓线,其中图(a)为LA,图(b)为LVM,图(c)为RA,图(d)为LV。

图5　基于本文方法与基于传统MI方法分割结果比较

3.3分割精度评价

本文把专业医师手动分割的图像作为金标准,将基于配准的分割算法分割出的心脏腔室结构与之对比,使用基于配准的分割结果和手动分割结果的体积重叠(Volume Overlap, VO)系数对每组实验中50小组的分割精度作出统计分析,体积重叠系数越接近于1表明基于配准的分割结果越接近于金标准的手动分割结果,该参数定义如下：

(5)

其中Vseg和Vgol分别为基于配准方法的分割体积和手动分割的体积。

表1为两组实验50小组图像的平均体积重叠系数统计结果,从表中数据可知基于本文提出的方法分割出的心脏结构和手动分割结果具有较高的相似性,换言之,本文提出的方法能够提高心脏分割精度。与之对应的箱线图如图6所示,相对于传统的基于互信息的配准方法而言,左心室、左心室肌、右心室和右心房等结构的重叠系数的平均值明显增大,其中右心房结构增加幅度为0.1,增加趋势最为明显。

表1　体积重叠系数比较

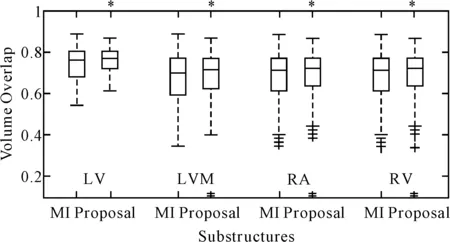
图6　心脏腔室结构的重叠系数比较

4　结语

本文提出灰度信息与形状特征信息相结合的方法提高心脏非刚性配准精度,从而提高全心脏分割精度。文中引进Marching cubes算法提取二值图像形状标记点,借助于笛卡尔图像构成标记点特征向量,通过匹配原则形成匹配的形状特征点对,依据特征点对之间的欧式距离改进配准过程中的相似性测度函数,换言之,使用特征点对之间的欧式距离作为互信息的约束项共同构成相似性测度函数。实验研究表明,基于本文提出的方法具有更好的配准结果,并且心脏腔室结构的分割精度明显提高,其与金标准的重叠系数明显增大,因此本文提出的方法优于传统的互信息配准方法。即使如此,在今后的研究工作中,必须进一步提高全心脏分割精度,才能将其应用于临床工作中。

[1] Hu SS, Kong LZ. Report on cardiovascular diseases in China. Encyclopedia of China Publishing House, Beijing,2010.

[2] Marwan M, Pflederer T, Schepis T. Accuracy of dual-source computed tomography to identify significant coronary artery disease in patients with atrial fibrillation:comparison with coronary angiography. Eur Heart J,2010,31(18):2230-2237.

[3] Xiahai zhuang, Kawal S, Rhode, Reza S, Razavi. A Registration-Based Propagation Framework for Automatic Whole Heart Segmentation of Cardiac MRI, IEEE transactions on image processing,2010,29:1612-1625.

[4] Lorensen, W. E and Cline, H. E. Marching Cubes: A High Resolution 3D Surface Construction Algorithm, Computer Graphics,1987,21(3):163-169.

[5] Warren Cheung and Ghassan Hamarneh, n-SIFT: n-Dimensional Scale Invariant Feature Transform[J], IEEE transactions on image processing,2009,18(9):2012-2021.

[6] Yongxin Zhou, Shuqian Luo, Medical Image Registration Based on Mutual Information of Feature Points, journal of computer-aided design and compute graphics,2010,14(7).

[7] Lorensen, W. E, Schroeder, W. J. and Zarge, Jonathan A., Decimation of Triangle Meshes, Internationa Conference on Computer Graphics and Interactive Techniques, Proceedings of the 19th annual conference on Computer Graphics and Interactive Techniques,1992:65-70.

[9] Klein S, Staring M, Murphy K, Viergever MA, Pluim JPW. Elastix: a toolbox for intensity-based medical image registration. IEEE Transactions on Medical Imaging,2010,29(1):196-205.

[10] L. Florack, The syntactical structure of scalar images, Ph.D. dissertation, Univ. Utrecht, Utrecht, The Netherlands,1993.

Nonrigid Registration of Cardiac DSCT Images by Integrating Intensity and Point-feature

CHEN ZhaoXIE Qinlan

(Institute of Biomedical Engineering, South-Central University for Nationalities, Wuhan430074)

A nonrigid registration combining mutual information(MI) with marching cubes shape points is proposed. Those points are regarded as a prior knowledge of the shape landmarks of cardiac structure. Mutual information combined with feature point pairs is used as the similarity measure function, namely a cost function. All feature descriptors of 15 dimensions are used to find out matched point pairs between marching cubes points in atlas intensity images and another points in the neighborhood of unseen images needing segmentation. The adaptive stochastic gradient descent(ASGD) optimization is used to obtain optimal registration parameters. Two groups of experiments show that the proposed method achieves higher registration accuracy than traditional MI and more accuracy anatomical information of the whole cardiac structure can be gained.

prior knowledge, MI, Marching Cubes, ASGD

2016年3月7日,

2016年4月24日

陈昭,女,硕士研究生,研究方向:医学图像处理。

TP391DOI:10.3969/j.issn.1672-9722.2016.09.037