基于集对分析和粗集理论的辐射源威胁等级判断*

谭　龙　潘继飞　杨　丽　吴惟诚

(电子工程学院信号与信息处理实验室　合肥　230037)



基于集对分析和粗集理论的辐射源威胁等级判断*

谭龙潘继飞杨丽吴惟诚

(电子工程学院信号与信息处理实验室合肥230037)

针对雷达告警系统中对未知辐射源信号告警不准确的问题,利用集对分析和粗集理论构造一个综合性评价模型,通过选择未知辐射源信号的多个属性指标,同时给出各属性指标的隶属度函数,然后在用熵值法确定各属性指标权重值的基础上,实现对未知辐射源信号的威胁等级排序。最后通过实例验证了该方法能对雷达数据库中未搜集的未知辐射源信号的威胁等级进行有效判定。

雷达告警; 集对分析; 粗集理论; 威胁等级

Class NumberTN953

1　引言

雷达告警系统中,在对辐射源信号进行识别时,如果是雷达数据库中已有的数据,则可以根据相应算法直接确定雷达的型号及其所在武器平台的相关信息,从而将准确信息反映给雷达操纵员,达到精确告警的目的。然而,随着现代科技的不断进步,各类新体制雷达发展迅速,在信号的调制样式、参数设置上更加灵活多变,仅靠日常的ELINT侦察搜集的数据,并不能完全囊括所有的雷达型号,再单纯地依靠数据库信息很难做到有效告警,这将极大影响我方装备的战斗力和生存能力[1]。

针对这个问题,本文利用集对分析和粗糙集理论建立一个综合性评价模型,结合情报侦察得到的相关数据,充分考虑辐射源的类型、距离、速度、所在武器平台性能等综合性因素后,从而对未知的雷达辐射源信号进行较准确的威胁等级判定[2],作为雷达信号精确识别的有益补充。

2　集对分析

为寻求一种恰当的方式来描述事物间的确定不确定关系,我国学者赵克勤于20世纪80年代提出了集对分析(Set Pair Analysis,SPA),即一种关于确定不确定问题同异反定量分析的统计数学方法。所谓集对,就是具有一定联系的两个集合所组成的对子,其核心思想是将研究对象之间的确定性与不确定性程度作为一个确定不确定系统,在某一问题背景下,从“同一性”、“对立性”、“差异性”角度入手对事物之间的联系、影响和制约关系进行辩证分析、定量研究和数学处理[3]。为更好地理解该方法,下面给出集对分析中最重要的一个概念——联系度:

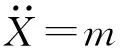
定义2问题背景W:“X和Y两个集合之间是否存在关系f”

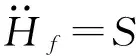
由上面三种情况,可引入“联系度”的表达式如下

(1)

式中i为差异度标记,根据讨论问题的不同,取值于之间[-1,1],通常取为1;j为对立度标记,通常取为-1。可将上式简记为

μ(X,Y)=a+bi+cj

(2)

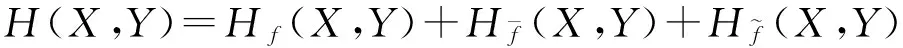
a+b+c=1

(3)

综上所述,不难看出联系度综合反映集对中的两个讨论对象X和Y的同异反程度,是集对分析方法中的核心问题。这里再给出联系度的三个运算规律:

(Ⅰ)设两个不同的联系度分别为μ1=a1+b1i+c1j和μ2=a2+b2i+c2j,则有:

μ1+μ2=a1+b1i+c1j+a2+b2i+c2j

=(a1+a2)+(b1+b2)i+(c1+c2)j

(4)

(Ⅱ)设两个不同的联系度分别为μ1=a1+b1i+c1j和μ2=a2+b2i+c2j,则有:

μ1×μ2=(a1+b1i+c1j)×(a2+b2i+c2j)

=(a1a2+b1b2+c1c2)+(a1b2+a2b1

+b1c2+b2c1)i+(a1c2+a2c1)j

(5)

(Ⅲ)设背景问题中的评价等级除同异反外还需做更细的划分,则有扩展式为

μ=a+b1i1+b2i2+…+bnin+cj

μ=a1+a2…+ak+b1i1+b2i2+…

+bnin+c1j1+c2j2…+cmjm

(6)

具体的展开形式需根据所讨论问题和评价目标来定(注:一般情况不讨论式(6)中的in)[4]。

3　粗糙集理论

信息时代,也是“大数据”时代,为能从搜集的海量数据中挖掘有用的信息,20世纪末,波兰学者Z.Pawlak提出粗糙集(Rough Sets)理论进行数据分析,在保证分类能力不变的前提下,通过知识约简得到问题的分类规则[5]。该理论最大的特点是无需凭借任何外在信息或先验知识,而是直接从所给数据中提取问题的决策知识,从而挖掘出隐层知识。为便于问题说明,这里给出几个定义:

(7)

定义6令P,Q⊆A,R∈P,若有posind(P)(ind(Q))=posind[P-{R}](ind(Q)),则称R为P中Q不必要的,否则称为必要的。因此,若P中的所有R均为Q必要的,则称P独立于Q。

设H⊆P,则H为P的Q约简当且仅当H为P的Q独立子族,且posH(Q)=posP(Q)时成立。P中所有Q必要的原始关系构成的集合称为P的Q核,记为coreQ(P)。

定义7令P,Q⊆A,当γp(Q)=|posP(Q)|/|U|=k时,称Q为k(0≤k≤1)度依赖于P,记为P⟹kQ,γp(Q)也称为Q的近似分类质量。

由以上给出的几条定义可以看出,粗糙集理论作为一种数据分析工具具有较好的挖掘能力,有助于发现数据的隐含信息,排除冗余信息,然而其不能处理较好的处理不精确的原始数据,因此将其与处理不确定问题的理论方法联合使用,有较好的互补性,提高了判断的效率和准确性[6]。

4　基于集对分析和粗集理论的综合评价模型

4.1模型描述

根据粗糙集理论的概念,提出多属性决策问题背景Q=(U,A,W,X),其中U={x1,x2,…,xn}表示论域,即待判定的威胁雷达;A={a1,a2,…,am}表示影响威胁的雷达的属性指标集;W={w1,w2,…,wm}表示属性指标的权重集,二者一一对应;X=(xkr)n×m表示决策矩阵,即雷达xk关于某项指标ar的量化值。则论域U和属性集A构成一个集对,问题背景Q即可描述为“所有待判定雷达的威胁等级与各属性指标之间的关联程度”[7]。

4.2区间数和模糊语言

为便于描述辐射源的威胁程度,首先引入区间数和模糊语言的概念,因为威胁指标往往不是一个固定值,而是在一定区间上,而威胁程度的大小也就反映在这些指标区间上,根据指标值的区间不同,威胁大小不同,所以需要模糊语言来进行客观描述。

定义8设有实数域R,令aL,aH∈R,且aL≤aH,则[aL,aH]表示闭区间数,[R]表示R上的全体闭区间数的集合;对于任意一点a,若a∈R,则认为其也是区间数,表示为[a,a]。

闭区间数有如下几条运算规律:

1) [aL,aH]+[bL,bH]=[aL+bL,aH+bH]

2) [aL,aH]·[bL,bH]=[aLbL,aHbH]

3) ∀λ∈R+,λ[aL,aH]=[λaL,λaH]

4) [aL,aH]÷[bL,bH]=[aL÷bL,aH÷bH]

定义9模糊语言是反映决策者对不确定、随机性问题的评价,评估标度为C={C1,C2,…,Cn},其中C1,C2,…,Cn对A(属性集合)达到有序分割的目的,且C1>C2>…>Cn。

常用的评估标度模糊语言如,五标度语言集L1={优,良,中,差,特差},其中优>良>中>差>特差;九标度语言集L2={特优,很优,优,较优,中,较差,差,很差,特差},其中特优>很优>优>较优>中>较差>差>很差>特差。

综上所述,用区间数来表示模糊语言,以五标度为例进行威胁程度的划分为:很高=[0.8,1],高=[0.6,0.8],中=[0.4,0.6],低=[0.2,0.4],很低=[0,0.2][8]。

4.3属性指标及其隶属度计算

敌方雷达对我方的威胁程度,主要可从雷达辐射源和雷达所在武器平台两个方面进行判断,这里主要考虑以下几个方面:

图1　雷达威胁等级的判断依据

由此属性集A={a,b,c,d,e,f,g,h,i,j,k}={CF,PRF,PW,DOA,天线特性,作战能力,距离,速度,高度,干扰能力,带弹情况},根据定义6对其进行约简求核,可知d,e,j,k可省去,仅留a,b,c,f,g,h,i便可判定雷达的威胁等级。

约简后的几项性能指标中,除了作战能力之外,都能够量化处理,因此采用模糊语言来描述作战能力,其他属性的隶属函数可分别由以下各式求得[9]:

1) CF隶属度函数:

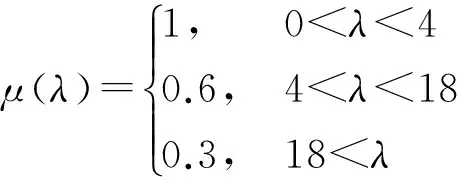
(8)

式中λ表示波长(cm),反映载频的大小。

2) PRF隶属度函数:

(9)

式中fr表示辐射源的重频(kHz)。

3) PW隶属度函数:

(10)

式中τ表示辐射源脉冲宽度(μs),其与威胁大小呈反比。

4) 作战能力

作战能力这一属性指标属于条件型属性,其很难用具体的数值进行量化,因此,利用模糊语言和区间数对其进行描述。这里采取五标度语言,具体将其分为:优[0.8,1]、良[0.6,0.8]、中[0.4,0.6]、差[0.2,0.4]、特差[0,0.2]。

5) 距离隶属度函数:

μ(r)=e-0.005r2, -30≤r≤30

(11)

式中r为目标距离(km)。

6) 速度隶属度函数:

μ(v)=1-e-0.005v

(12)

式中v为目标速度(m/s)

7) 高度隶属度函数

(13)

式中h表示目标高度(km)。

4.4应用信息熵确定指标权重

每个属性指标对不同目标的威胁大小是通过权重大小体现的,基于信息熵的指标权重值的确定,就是通过不同属性指标传递给决策者信息量的大小来计算权重的,具体方法如下[10]:

1) 为消除不同量纲对计算结果的影响,首先将决策矩阵(xkr)n×m转化为标准化矩阵(rkr)n×m的计算:

(14)

2) 不同属性指标传输给决策者的信息熵集E={E1,E2,…,Em},各属性指标包含的信息量具体计算如下:

(15)

3) 依据信息论中相对熵的计算公式求权重集w={w1,w2,…,wm}。

(16)

4.5联系度及威胁排序的确定

μ(xkr,1)=akr+bkri+ckrj

(17)

由联系度和区间数的运算法则,可得到每个待评价目标的加权平均威胁度:

(18)

此时其对应的联系度为μk=ak+bki+ckj。

然后根据准则相对贴近度dk的定义,计算目标xk与威胁程度最高之间的贴近程度,其计算公式为

(19)

由dk值的大小便可判断目标威胁程度的大小,值越大,威胁也就越大[11]。

4.6具体判定步骤

步骤1搜集、整理截获辐射源信号的参数值,分析情报侦察得到的数据;

步骤2确定分析目标即论域U,属性指标集A,写出混合型决策矩阵X;

步骤3通过计算属性指标的隶属度,求出混合型决策矩阵的威胁隶属度区间决策矩阵;

步骤5计算目标联系度μk,确定威胁贴近度dk的大小,判断所评估目标的威胁大小顺序。

5　实例分析

上面建立了基于集对分析和粗糙集理论的综合评价模型,并对将要用到的概念进行了定义和说明,为验证该模型的有效性,现将其用于未知雷达辐射源的威胁等级判定,根据判断结果进行具体分析。

假定在某一时刻,告警接收机截获到五个未知雷达辐射源信号,测出其信号参数和所在武器平台的运动状态等属性指标如下所示(为便于表示,就依次用a,b,c,f,g,h,i分别表示CF、PRF、PW、作战能力、距离、速度、高度)。

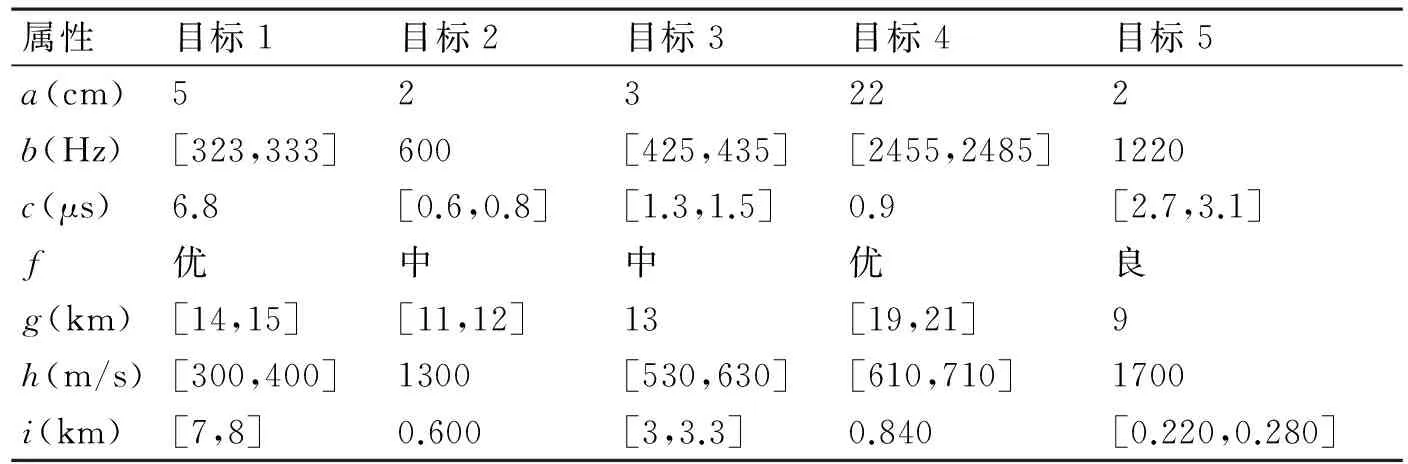
表1　待评估目标的多属性参数区间值

根据各属性指标求隶属函数的计算公式,求出威胁隶属度区间决策矩阵,用表2表示。

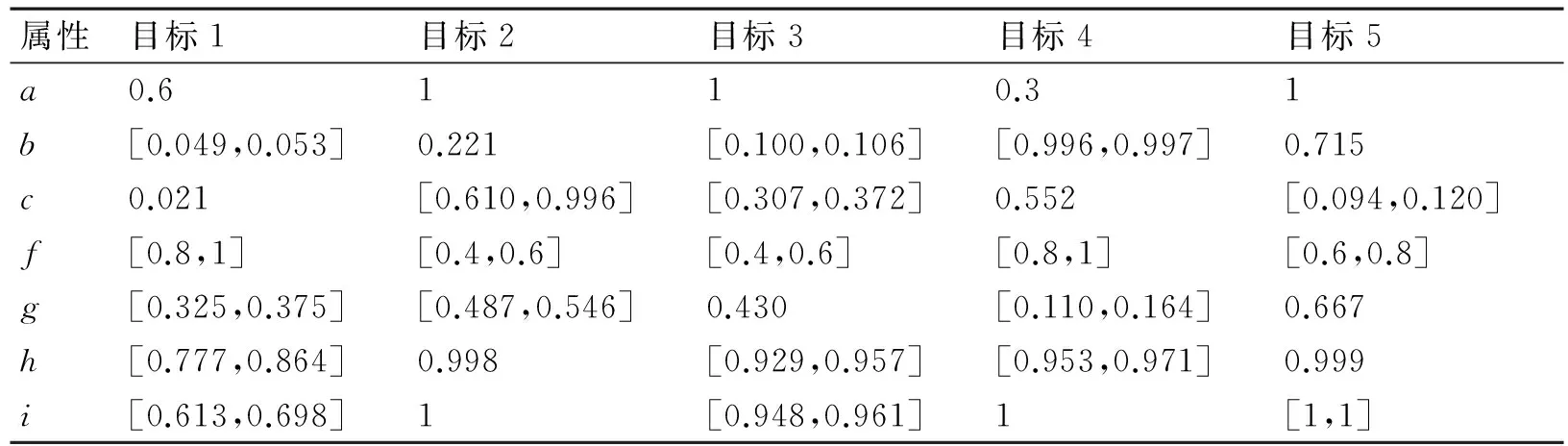
表2　待评估目标威胁隶属度矩阵

表3　各属性指标对应的权重区间

然后根据式(18)的计算方法,可以求出每个待评价目标的加权平均威胁度,如表4。

表4　待评价目标的加权平均威胁度

在此基础上,再由式(17)中a,b,c三个参数的求法,将上表中的威胁区间数转化为集对分析中的集对数:

(20)

最后根据贴近度的定义计算式(19),求得各待评价目标的贴近度dk分别为dk=(0.510,0.765,0.640,0.710,0.773),则五个待评价目标的综合威胁程度排序为:x5>x2>x4>x3>x1。达到了预期的对未知雷达辐射源威胁等级进行评估的目的。

6　结语

本文根据目前雷达告警系统中对未知辐射源信号不能进行有效告警的问题,提出利用集对分析和粗集理论建立的综合评价模型,用集对分析对不确定问题的判断优势和粗集理论属性约简的特点,在情报侦察得到的目标辐射源信号的多属性指标信息基础之上,较全面地分析未知辐射源信号的威胁程度,最终给出准确的判断结果,从而保证告警接收机能够对战场截获的未知辐射源信号进行准确告警的能力。最后通过实例,验证了利用该模型进行威胁判断的可行性,为战场告警提供了有益补充。

[1] 周帆,陈兴凯,韩壮志,等.机载雷达告警接收机的现状及技术发展趋势[J].飞航导弹,2014(2):41-46.

ZHOU Fan, CHEN Xingkai, HAN Zhuangzhi, et al. Status and Trends of the Airborn Radar Warning Receiver[J]. Aerodynamic Missile Journal,2014(2):41-46.

[2] 曲长文,何友,马强.应用多属性决策的威胁评估方法[J].系统工程与电子技术,2000,22(5):26-29.

QU Changwen, HE You, MA Qiang. Threat Assessment Using Multiple Attribute Decision Making[J]. System Engineering and Electronics,2000,22(5):26-29.

[3] 赵克勤.集对分析及其初步应用[M].杭州:浙江科学技术出版社,2000.

ZHAO Keqin. Set Pair Analysis and Its Preliminary Application[M]. Hangzhou: Zhejiang Science and Techology Press,2000.

[4] 胡华强.应用集对分析理论的辐射源威胁评估与排序方法[C]//第三届中国智能计算大会论文集,济南,2009:330-334.

HU Huaqiang. Radiation Source Threat Assessment and Ranking Method Using SPA Theory[C]//Proceeding of the third China Intelligent Computing Conference, Jinan,2009:330-334.

[5] 李超伟.基于粗糙集的特征选择算法研究[D].太原:山西大学,2013.

LI Chaowei. Recearch on Feature Selection Algorithm Based on Rough Sets[D]. Taiyuan: Shanxi University,2013.

[6] 卜雪妮,邓胜利.粗糙集理论在雷达识别中的应用[J].电光与控制,2009,16(11):80-83.

PU Xueni, DENG Shengli. Application of Rough Set Theory in Radar Target Recognition[J]. Electronics Optics & Control,2009,16(11):80-83.

[7] 高黎,何晓晔,刘小兵,等.基于集对分析与粗糙集理论的综合评价模型[J].后勤工程学院学报,2009,25(4):81-85.

GAO Li, HE Xiaoye, LIU Xiaobing, et al. A Comprehensive Evaluation Model Based on SPA and Rough-set Theory[J]. Journal of Logistical Engineering University,2009,25(4):81-85.

[8] 栗飞,刘博,徐海峰.基于集对分析的混合型多属性目标威胁评估[J].海军航空工程学院学报,2012,27(2):219-222.

LI Fei, LIU Bo, XU Haifeng. Threat Assessment of Hybrid Multi Attribute Target Based on SPA[J]. Journal of Naval Aeronautical and Astronautical University,2012,27(2):219-222.

[9] 李楠,曲长文,苏峰,等.基于粗糙集的雷达辐射源信号识别[J].航天电子对抗,2010,26(4):8-10.

LI Nan, QU Changwen, SU Feng, et al. Radar emitter signal recognition based on rough set[J]. Aerospace Electronic Warfare,2010,26(4):8-10.

[10] 孟宪萌,胡和平.基于熵权的集对分析模型在水质综合评价中的应用[J].水利学报,2009,40(3):257-262.

MENG Xianmeng, HU Heping. Application of SPA Analysis Model in Comprehensive Evaluation of Water Quality Based on Entropy Weight[J]. Journal of Hydraulic Engineering,2009,40(3):257-262.

[11] 杨春玲,张传芳.基于集对分析的混合型多属性决策方法的研究[J].数学的实践与认识,2008,38(21):134-142.

YANG Chunling, ZHANG Chuanfang. Research on the Hybrid Multi Attribute Decision Making Method Based on SPA[J]. Mathematics in Practice and Theory,2008,38(21):134-142.

Judging of Radiant Point Menace Based on SPA and Rough-set Theory

TAN LongPAN JifeiYANG LiWU Weicheng

(Laboratory of Signal and Information Processing, Electronic Engineering Institute, Hefei230037)

In order to solve the problem that the radar warning system doesn’t have high accuracy when the research target is unknown radiant point, a comprehensive model is proposed based on SPA(Set Pair Analysis) and rough-set theory. Several attribute indexes are selected, and their own membership function is given, then the menace grade of all indexes are ascertained with entropy value method. On the basis of this, the unknown radiant points’ menace level are assessed. The example shows the practicability of the model.

radar warning, SPA, rough-set theory, menace grade

2016年3月12日,

2016年4月20日

谭龙,男,硕士研究生,研究方向:雷达与雷达对抗,信号处理。

TN953DOI:10.3969/j.issn.1672-9722.2016.09.014