全等之后见精彩
□左效平
全等之后见精彩
□左效平
全等三角形既是独立的数学知识,也是重要的学习工具,如能灵活应用这一强有力的数学工具,将会充分享受三角形全等后带来的精彩,真正领悟数学的魅力,感悟数学的奇妙.
一、全等后辨析结论正误
例1如图1,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:
①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF.
其中正确的结论共有().

图1
A.4个B.3个
C.2个D.1个
分析:由BF∥AC,得∠C=∠CBF,因为BC平分∠ABF,所以∠ABC=∠CBF,所以∠C=∠ABC,所以AB= AC,因为AD是△ABC的角平分线,所以BD=CD,AD⊥BC,②③正确.
在△CDE与△DBF中,
所以△CDE≌△BDF,
所以DE=DF,CE=BF,
结论①正确.
因为AE=2BF,所以AC=3BF,
④正确.
解:选A.
二、全等后证明线段相等
例2如图2,已知点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,EF=FD.求证:AD=CE.
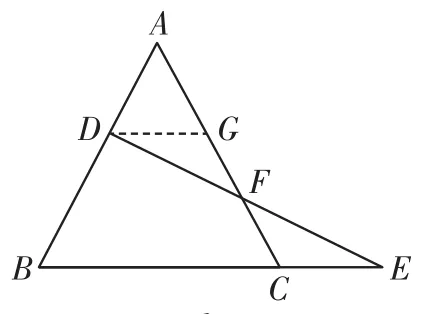
图2
分析:作DG∥BC交AC于G,先证明△DFG≌△EFC,得出GD= CE,再证明△ADG是等边三角形,得出AD=GD,即可得出结论.
证明:如图2所示,作DG∥BC交AC于G,则∠ADG=∠B,∠AGD=∠ACB.因为△ABC是等边三角形,所以△ADG是等边三角形,所以DG=AD.
因为DG∥BC,所以∠GDF=∠CEF,∠DGF=∠ECF.
在△DGF和△ECF中,
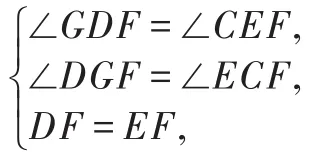
所以△DGF≌△ECF,
所以CE=GD.
因为GD=AD,所以AD=CE.
三、全等后判定三角形的形状,探求生成新角的度数
例3已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图3,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;

图3
(2)如图4,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.
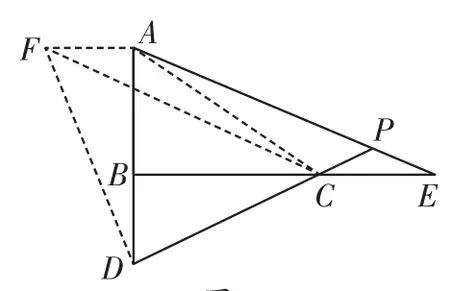
图4
分析:(1)利用SAS证明△AFD和△BDC全等,再利用全等三角形的性质得出FD=DC及∠FDA=∠DCB,即可判断三角形的形状.
(2)作AF⊥AB于A,使AF=BD,连结DF、CF,利用SAS证明△AFD和△BDC全等,再利用全等三角形的性质得出FD=DC,∠FDC=90°,即可得出∠FCD=∠APD=45°.
解:(1)△CDF是等腰直角三角形,理由如下:
因为AF⊥AD,∠ABC=90°,
所以∠FAD=∠DBC=90°.
在△FAD与△DBC中,
所以△FAD≌△DBC(SAS),
所以FD=DC,∠FDA=∠DCB.
因为∠BDC+∠DCB=90°,
所以∠BDC+∠FDA=90°,
所以△CDF是等腰直角三角形.
(2)作AF⊥AB于A,使AF=BD,连结DF、CF,如图4.
因为AF⊥AD,∠ABC=90°,
所以∠FAD=∠DBC=90°.
在△FAD与△DBC中,

所以△FAD≌△DBC(SAS),
所以FD=DC,∠FDA=∠DCB.
因为∠BDC+∠DCB=90°,
所以∠BDC+∠FDA=90°,
所以△CDF是等腰直角三角形,
∠FCD=45°.
因为AF∥CE,
所以∠FAC=∠ECA.
因为CE=BD,BD=AF,
所以AF=CE.
在△FAC与△EAC中,

所以△FAC≌△ECA,
所以∠FCA=∠EAC,
所以AE∥CF,
所以∠ADP=∠FCD=45°.
四、全等后判定两线的位置、数量关系
例4如图5,已知:在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.
(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.
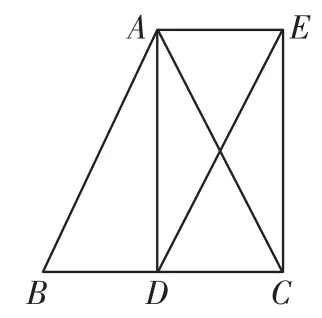
图5
分析:(1)运用AAS证明△ABD≌△CAE.
(2)证明△ADE≌△ECA,AC= DE,结合AB=AC,得证AB=DE;证明∠ABC=∠ACB=∠EDC,可证明AB∥DE.
证明:(1)因为AB=AC,所以∠B=∠ACD,因为AE∥BC,所以∠EAC=∠ACD,所以∠B=∠EAC.
因为AD是BC边上的中线,所以AD⊥BC,因为CE⊥AE,所以∠ADC=∠CEA=90°.
在△ABD和△CAE中,

所以△ABD≌△CAE(AAS).
(2)AB=DE且AB∥DE.
理由如下:连接DE,因为AD⊥BC,AE∥BC,所以AD⊥AE,因为CE⊥AE,所以∠DAE=∠CEA=90°.
由(1)知△ABD≌△CAE,
所以AD=CE,
在△ADE和△ECA中,
所以△ADE≌△ECA,
所以DE=AC,
因为AB=AC,所以DE=AB.
因为△ADE≌△ECA,
所以∠ADE=∠ACE,
所以∠EDC=∠ACB,
所以∠EDC=∠B,
所以AB∥DE.
所以二者的关系是AB=DE且AB∥DE.

