绳-船模型的拓展研究

何述平

(西北师范大学教育学院物理教育研究所　甘肃 兰州　730070)



绳-船模型的拓展研究

何述平

(西北师范大学教育学院物理教育研究所甘肃 兰州730070)

基于绳-船模型拓展性地探究了斜绳上点的速度、加速度，结果表明：斜绳上各点的速度、加速度的大小、方向均不同；深化了绳-船模型的运动学认识．

绳-船模型斜绳上点速度加速度拓展

1　引言

绳-船模型是典型的运动学问题：如图1，岸上一人用绕过定滑轮的不可伸长的轻绳以匀速率v0拉湖面上与绳相连的船靠岸，当绳与水平面成θ角时，求船的速度、加速度．从普通物理用直角坐标分量法可简便解决[1]．因绳、船连动，则连接船的斜绳端点的速度、加速度与船的相同；那么，斜绳上点的速度、加速度如何？有怎样的特点？就此进行相应的探究，以期拓展、深化绳-船模型的运动学认识，并为教学奠定基础．

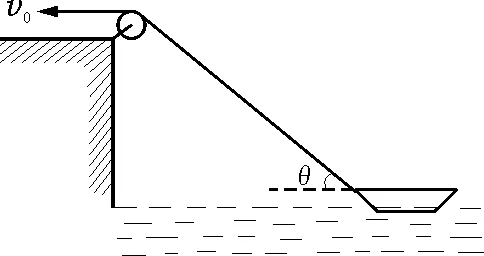
图1　绳-船模型

2　探究

基于绳-船模型，依次探究斜绳端点、斜绳上点的速度、加速度．

2.1斜绳端点的速度加速度

湖岸为参考系，斜绳与滑轮相切处为原点，建立平面直角坐标系O-xy，如图2；连接船的斜绳端点A为研究对象(视作质点)，位置坐标为(xA,yA)；取rA，θ为参量，则有

xA=rAcosθ

(1)

yA=rAsinθ

(2)

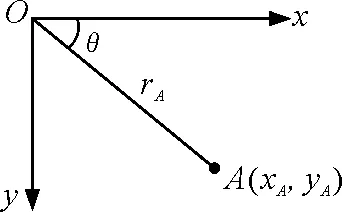
图2　点A的直角坐标

式中xA，rA，θ均是时间t的变量，而由题设知yA=c为恒量(因绳端A随船沿湖面水平向左运动)；对t求导得

(3)

(4)

依题意：绳缩短，则有

(5)

由式(3)、(4)、(5)得

(6)

(7)

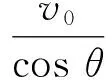
由式(6)、(7)得端点A的加速度[1]

(8)

式(6)、(8)中的负号表明：斜绳端点A的速度、加速度的方向均沿x轴反向．

2.2斜绳上点的速度加速度

有定性说明斜绳上各点的速度的大小、方向都不相同，但斜绳上各点的速度在绳上的投影都相同，等于拉绳的速度[1]；而未能依据位移、速度概念细致推证，难免令人费解.鉴于此，先定性推证，再定量探究．

2.2.1斜绳上点的速度特点

斜绳与滑轮相切处O为参考点(惯性系)，经时间Δt，船沿湖面由A点运动到B点，斜绳上一点P相应由P点运动到M点，位移矢量为Δr，取ON=OM，则点P的位移矢量三角形为ΔPNM，如图3(a)；Δt足够短或趋于零时，分位移Δr2垂直于分位移Δr1(Δr可等效为相对于参考点O的位置矢量r[图3(a)中未画出]的大小变化即分位移Δr1和方向变化即分位移Δr2)．因此，点P的运动自然是沿绳的分运动、垂直绳的分运动的合运动；即点P的速度vP是沿绳的分速度v1，垂直绳的分速度v2的合速度，如图3(b)；但点P的速度方向不再沿水平向左．从而定性推知：斜绳上各点的速度的大小、方向都不相同，但斜绳上各点的速度在绳上的投影都相同，等于拉绳的速度．

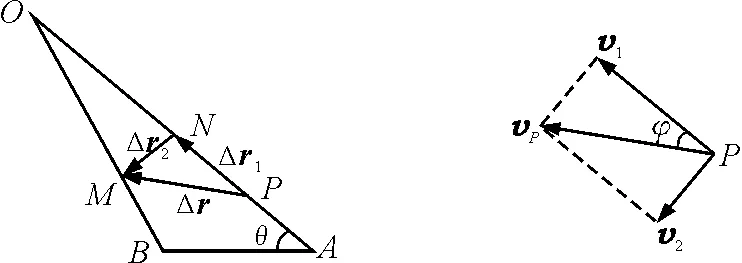
(a)点P的位移矢量　　　　　(b)点P的速度矢量

2.2.2直角坐标系下斜绳上点的速度、加速度

(1)直角坐标系下斜绳上点的速度

参考系、直角坐标系见图2，斜绳上一点P为研究对象(视作质点)，位置坐标为(xP,yP)，点P与斜绳端点A共线，则有约束方程

xP=rPcosθ

(9)

yP=rPsinθ

(10)

式中xP，yP，rP，θ均是时间t的变量，求导得

(11)

(12)

式中P是斜绳上的点，且绳缩短，则有

(13)

由式(11)～(13)和式(7)得

(14)

(15)

即P点的速度为

(16)

于是有

(17)

(18)

式(18)的结果同端点A的式(6)．由式(16)得vP的大小、与水平面夹角

(19)

(20)

式(19)、(20)表明：vP，α均是rP的函数，即斜绳上各点的速度的大小、方向均不同；进而得(由题设知：

(21)

(22)

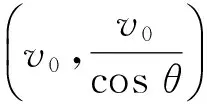
(2)直角坐标系下斜绳上点的加速度

由式(16)及式(5)、(7)、(13)得P点的加速度

(23)

于是有

(24)

(25)

式(25)的结果同端点A的式(8)．由式(23)得aP的大小、与水平面夹角正切

(26)

(27)

式(26)、(27)表明：aP，tanβ均是rP的函数，即斜绳上各点的加速度的大小、方向均不同；进而得

(28)

(29)

令式(28)等于零，得

(30)

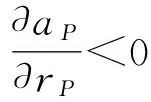
(31)

2.2.3极坐标系下斜绳上点的速度、加速度

(1)极坐标系下斜绳上点的速度

(32)

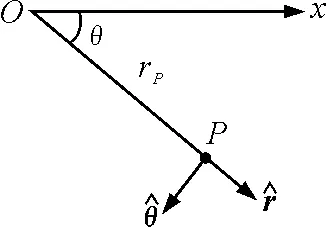
图4　点P的极坐标

则P点的速度为

(33)

由旋转矢量导数[2]、式(7)得

(34)

(35)

由式(33)、(13)、(34)得

(36)

式(36)表明：P点的速度vP是沿绳收缩的分速度

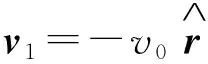
(2)极坐标系下斜绳上点的加速度

由式(36)、(34)、(35)、(5)、(7)、(13)得P点的加速度

(37)

于是有

(38)

(39)

由式(37)得aP的大小同式(26)，与斜绳夹角正切

(40)

式(26)、(40)表明：aP，tanφ均是rP的函数，即斜绳上各点的加速度的大小、方向均不同；由式(37)、(30)得极小值时加速度

(41)

3　讨论

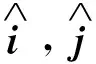
就物理学方法而言，直角坐标参量法涉及导数、矢量表示等方法；极坐标法涉及导数、矢量表示、单位矢量导数、矢量叉乘等方法．

4　结语

基于绳-船模型拓展性地探究了斜绳上点的速度、加速度，给出了定量表达式，并界定了取值；讨论了直角坐标参量法、极坐标法的特点；深化了绳-船模型的运动学认识，为教学奠定了基础．呈现了拓展普通物理运动学基本问题的一个实例．从基本问题到拓展问题，反映了提出问题能力；而提出问题能力的培养是教学目标之一；因此，依据教学实际适度让学生拓展适宜的基本问题，应是培养其提出问题能力的有效教学策略．

1胡盘新，孙迺疆．普通物理学(第5版)习题分析与解答．北京：高等教育出版社，2003．9～10

2Kleppner D，Kolenkow R J．力学引论．宁远源，等译．北京：人民教育出版社，1980．33～35，43

Extending Research on Rope-boat Model

He Shuping

(Research Institute of Physics Education，College of Education，Northwest Normal University，Lanzhou,Gansu730070)

Based on the model of rope-boat，the velocity and acceleration of a point of slanting rope are extensively explored，the results show that the size and direction of velocity and acceleration of each point of slanting rope are different；recognizing of kinematics of the model of rope-boat is deepened．

rope-boat model；point of slanting rope；velocity；acceleration；extending

2016-03-17)