基于GIS的琼州海峡潮流空间插值模型比较研究

丁　杰，汪小勇，王海峰，武　贺，姜　波，陈利博，陈家庆，石　勇，蔡晓晴

（国家海洋技术中心，天津　300112）

基于GIS的琼州海峡潮流空间插值模型比较研究

丁杰，汪小勇，王海峰，武贺，姜波，陈利博，陈家庆，石勇，蔡晓晴

（国家海洋技术中心，天津300112）

为了客观准确地反映海洋潮流空间分布特征，文中选取琼州海峡表层大潮流速数据，运用泛克里金插值法中的球状、指数、高斯和有理二次方程式4种不同半变异模型进行拟合插值，采用交叉验证和点验证法，通过对比4种半变异模型4个指标精度，研究结果表明在琼州海峡区域，有理二次方程式模型对表层大潮流速拟合效果最优，该研究为描述琼州海峡潮流空间分布和建立精确插值模型提供依据。

琼州海峡；空间插值；潮流；泛克里金法

潮流是由月球和太阳引潮力引起的周期性海水往复运动的现象，在水道中形成的高密度潮流能是一种非常有发展潜力的可再生能源。随着世界能源的日益短缺和环境不断恶化，促使各国加快绿色能源的开发利用，近年来潮流能开发利用技术发展日益成熟，如何准确描述潮流空间分布规律，对潮流能资源的有效开发意义重大。

在大量文献中，国内很多学者运用地统计学在气象和生态等领域进行插值方法与模型拟合比选［2-10］。张余庆等［2］对江西1976-2005年平均降水量空间规律进行分析研究，运用泛克里金插值法，对比球状、指数、高斯和有理二次方程式4种模型对降水量的拟合优度，研究表明指数模型最佳；王常森等［3］对淮北平原2009年平均降水量进行分析研究，运用普通克里金插值法，不仅对比球状、指数和高斯3种模型交叉验证的精度，同时考虑了水文专业的特殊性，比选出球状模型更优。由此可见，插值模型的比选优度受地域和时间尺度的影响，不仅如此，不同插值方法的使用也会对研究结果产生差异。然而，在已有文献中运用地统计学针对海洋水文要素插值模型的比选研究甚少，因此为了研究潮流的空间分布规律与不同插值模型对插值结果影响，本文选取了琼州海峡表层大潮平均流速数据［1］，讨论了针对该区域潮流要素插值法最优选择，对比不同模型半变异函数的插值精度，结合了海洋水文的精度指标要求，为描述潮流空间分布和建立精确插值模型提供依据。

1　研究区域概况与数据

1.1琼州海峡概况

琼州海峡是位于中国海南岛与雷州半岛之间的水道，为中国三大水道之一。它西接北部湾，东连南海北部，呈东西延伸，地处北纬20°N～20°10′N、东经110°05′E～110°30′E，是东南沿海进入北部湾的海上要塞。

1.2数据来源与预处理

本研究选取了琼州海峡大潮表层流速数据［1］，首先对样本进行预处理，使用冯罗诺多边形聚类法［8］和直方图相结合，剔除明显的异常值（极大值和极小值）后遴选出58个样本点，选取样本点中50个建模并进行交叉验证，8个点作为验证点进行试验。其中2个验证点分别位于海峡南北的海陆边缘处，其余6个验证点分别位于海峡的东西两侧与中部。数据的地理坐标采用CGCS2000大地坐标系，投影系统采用高斯-克吕格3°带，中央经线111°E，建立空间数据库，其空间分布情况如图1所示。

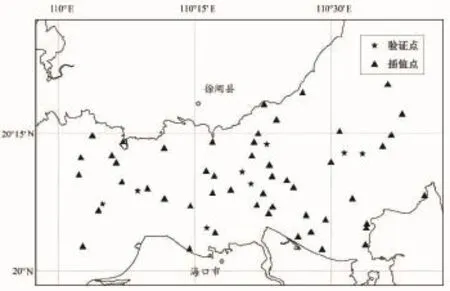
图1　琼州海峡插值点与验证点分布图

2　数据的预处理

2.1空间自相关检验

地统计学是以区域化变量理论为基础，以变异函数为工具，研究那些在空间分布上既有随机性又有结构性，或空间相关和依赖的一门科学［10］。运用其分析的前提是样本间具有空间相关性，首先对样本之间的自相关性进行检验。本文采用莫兰指数检验法，莫兰指数取值范围为-1～1，值越接近1表示该研究区域单元间属性值越接近，相关性越大［8］。经计算流速值的莫兰指数为0.56，数值表明琼州海峡大潮表层流速具有中等偏强的空间自相关性，适宜选用地统计学方法进行建模计算。

2.2数据统计分析

为了正确、合理地对空间样本点数据进行地统计分析和建模，了解数据是否满足线性克里金插值条件，首先对样本的频率分布、是否存在全局趋势检验。其方法是通过频率分布图、正态QQ图、趋势图对数据的统计分布查看。线性克里金插值法通常要求数据符合正态分布，否则在插值过程中会产生比例效应，抬高基台值和块金值，使变异函数发生畸变，增大估值误差［5］。根据数据统计表明：区域内流速值区间为20.83～176.82 cm/s，均值为93.58 cm/s，中位值为97.59 cm/s，两者基本接近，偏度0.61为正偏（图2直方图）接近于0，通过了K-S正态分布检验，检验p值0.2，符合正态分布。图3正态QQ图表明数据整体分布接近直线，基本成标准正态分布。

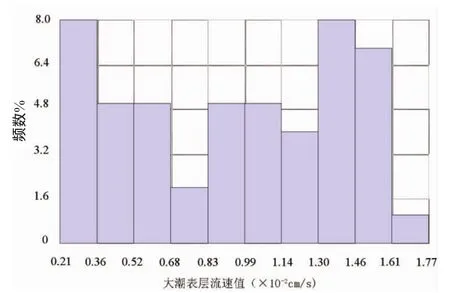
图2　直方图

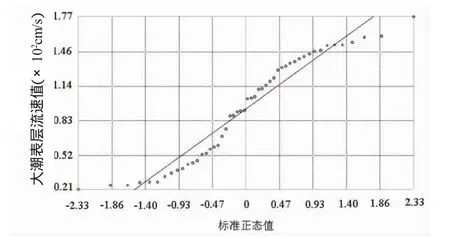
图3　标准正态QQ图

空间趋势如图4所示，流速具有较强的空间趋势，Y轴代表北方，X轴代表东方，Z轴代表流速值，侧面两条是数据投影点的二次多项式拟合曲线。投影曲线在南北与东西正交平面上呈倒“U”型，趋势表明潮流西高东低，该特征与研究区域盛行西南季风有关；南北方向流速中高两端低，该特征与地形周高中低有关；潮流最大值出现在水道中部，最小值在海陆交界附近。

图4　空间趋势分析图

3　潮流的空间结构分析

3.1半变异函数的计算

半变异函数能够反映区域变量的空间变化特征，在一维情况下，二阶平稳假设或本征假设的基础上，样本变差函数可通过式（1）［11］计算：

式中：r（h）为按步长h归类样点的平均半变异；N（h）为按方向归类样点对的个数；Z（xi）-Z（xi+h）为任意样本两点相距h的差值。对于样本非规则二维分布的情形，常用的方法是给定某一搜索方向的角度容差、距离容差，求得该方向上的变差函数［3］。

根据式（1），首先对样本按一定的步长分组，步长的选择对半变异函数有重要的影响，一般而言，步长过大会掩盖小尺度的空间自相关；过小将会出现空分组，不能反映组内的平均变异情况。本研究的样本为不规则分布，分组基于步长乘以步长组数小于等于所有采样点最大距离1/2的原则［11］。在研究区域内，东西方向样本点最远约68 km，考虑以上因素，确定步长为3.0 km，步长组为12，搜索带宽为3.2 km，搜索角度容差为45°。在半变异云图中（图5）观察，r（h）在120°方向变异程度比其它方向上强，它在120°和30°两个方向上具有不同的变程值，呈各向异向性［15］，30°方向为主变程，总套合结构是2个方向函数线性变换后转化为各向同性后的套合。即式（2）：

图5　不同方向的半变异云图

3.2不同变异函数模型的拟合

在研究样本自相关性后，应建立合适的函数模型，将对区域内全部有效结构信息作定量化概括。为了探讨基于不同半变异模型对琼州海峡表层流速的拟合精度，本文选取了4种模型进行拟合实验，分别是球状、指数、高斯和有理二次方程式。由此获取4种模型的变异函数的特征值（表1）。

表1　4种变异函数拟合的特征参数

块金值的产生通常有两种，一是由于样点间的距离大于微观结构的范围而产生，较大的块金值表明在研究尺度上存在较强的随机变异；二是测量误差，二者共同产生了块金值，误差会随块金值增大而增大［5］。由表1得知球状和指数模型在近距离处实验变差权重更大，拟合后的块金值为0，表明变量存在的均是结构性变异，不存在与空间无关的随机性因素；有理二次方程式和高斯模型拟合时出现块金值，存在块金效应，表明变量中存在较小随机变异。基台值反映了区域变化幅度的大小，即区域变化量变异的强弱，4种模型的基台值变化不大，且本身对插值结果影响很小。变程反映了区域变化量空间变异范围，4种模型的主、次变程差异很大，有理二次方程式的主变程38.4 km为4种中最大，高斯模型为19.26 km最小。综上所述，由于海洋潮流的形成过程受多物理因素影响，本身处于一个时刻变化的动态过程，增加了其变异的不确定性，依据最小块金原则［14］，由于高斯模型块金值过高，初步判定球状、指数和有理二次方程式模型拟合效果更优。

4　空间插值与分析检验

4.1插值法选取

克里金法是以空间自相关为基础，利用数据和半方差函数的结构性，对区域变化量的未知采样点进行无偏估值的插值方法［3］。目前，常用的单要素线性克里金插值法有以下几种类型：简单克里金、普通克里金、泛克里金等。简单克里金、普通克里金法假设区域化变量期望为一常数，区别在于期望值是否已知，二者更适用整体上研究区域变化量存在漂移，但在较小的局部范围平稳的要素［11］，同时林忠辉等［9］研究表明，普通克里金法插值存在平滑效应，在要素变化起伏比较大的区域效果不理想，消除了较小范围的变化趋势，因此采用此插值法不适合。泛克里金法假设数据存在主导趋势，可用确定的多项式表示空间位置与数据的关系，而后将多项式与样本的残差进行克里金分析，最后将趋势面与残差分析的克里金结果求和［12］。在本研究区域中由于地形和季风的影响，潮流在小范围变化较强，要素与空间位置存在整体趋势可用二阶多项式表示，由此可见采用泛克里金法优于其它两种方法。

4.2插值模型比较

运用泛克里金法分别采用4种不同的半变异模型对潮流进行拟合，等值线分级为25 cm/s，50 cm/s，75 cm/s，100 cm/s，125 cm/s，175cm/s，插值结果图见图6。从4种变异模型的插值图看，均符合空间趋势的分析结果，即潮流东高西低，南北方向中高两端低的整体趋势。对比插值结果图，4个模型结果最明显差别在于：球状和指数模型的插值结果未出现大于175 cm/s的区域。从样本中分析，位于水道中部21点位置为176.82 cm/s，因此高斯和有理二次方程式模型插值结果图更准确地拟合了小范围潮流变化的差异，较球状和指数模型插值结果更优。

将有理二次方程式与高斯模型的结果图比较，高斯模型的精度较差，原因在于27点样本值为159.15 cm/s，在高斯结果图中它位于等值线125～150 cm/s之间。将4个插值图进行综合比较，有理二次方程式模型插值结果较其它3种差别最大，其它3种模型结果在13，33，38，43，39，23处形成一个闭合的125 cm/s等值线，而有理二次方程式的结果将这6个点分割成3个125 cm/s的等值线，从分割点25，35，39处分析，3个点均在合理的等值区间。综上所述，在4种模型的插值结果中，有理二次方程式模型结果更优。不同模型拟合的效果对插值精度的影响还需通过后续交叉验证来检验。

图6　4种半变异模型插值结果

4.3结果检验

4种模型在该区域插值结果已进行定性分析，为了验证模型结果的精确性和可靠性，还需用客观的方法量化验证。本文采用4种验证指标评价模型的无偏性和误差的不确定性。即：平均预测误差（ME）、平均标准误差（ASE）、均方根预测误差（RMSE）和标准化均方根预测误差（RMSSE）。其计算公式分别为：

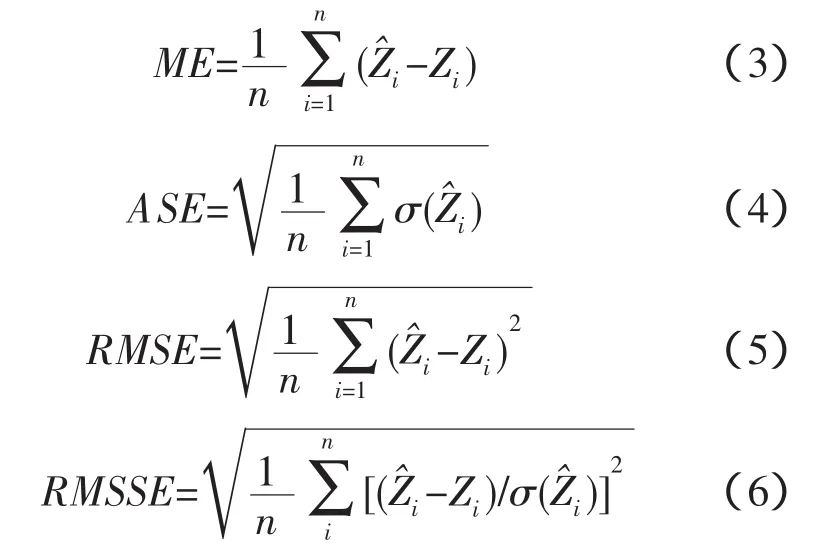
（1）平均预测误差越接近于0，预测误差无偏性越优。

（2）平均预测误差与均方根预测误差越小越优，同时平均预测误差越接近于均方根预测误差，即误差的不确定性越小，预测结果越准确。

（3）标准化均方根预测误差反映估值对变异性的预测情况，其值接近于1越优。

为此本文采用交叉验证和验证点法对4种模型插值结果进行验证，同时交叉验证时考虑了海洋水文的特殊性，指标参考了海洋调查规范第2部分［15］：海洋水文观测中海流观测的准确度要求：水深小于等于200 m海域，流速小于100 cm/s时，准确度为±5 cm/s；流速大于等于100 cm/s时，准确度为± 5%。4种模型的指标统计见表2。

由表2交叉验证结果可和，4个模型的平均预测误差的差别不大，其中指数模型的最小；对比平均标准误差和标准均方根误差，指数模型的均方根预测误差为21.13，平均标准误差为33.19，拟合误差的不确定性最大，高斯模型的平均标准标误差与均方根预测误差之间差值最小为1.27；对比标准化均方根预测误差，有理二次方程式模型的值最接近1，为0.98。同时，对比二者的误差范围百分比，4个模型对小于100 cm/s流速值拟合的精度效果均不理想，球状模型的百分比最低为28%；对比大于等于100 cm/s流速值，指数模型的最低为52%。

表2　4种模型的交叉验证结果

根据表2的指标参数，每种指标的最优模型均不同，无法比选出结果。因此，为了综合考虑每种指标，采用指标排名相加判定，排名和越小模型精度越好（表3）。

表3　4种模型交叉验证的指标排名结果

由表3可知，有理二次方程式的指标排名和最小，高斯模型的指标排名和与有理二次方程式最接近，为了进一步区分二者，需进行验证点验证。由于验证点数量较少，误差百分比的指标意义不大，因此仅采用4种指标参数对比验证。

表4　4种模型的验证点结果

表5　4种模型验证点的指标排名结果

由表4～表5验证点的结果可知，高斯和有理二次方程式模型的指标排名和相等。综合考虑高斯模型在27点处的误差和块金值过高，比选出有理二次方程式模型更能较准确地反映琼州海峡表层大潮流速的空间分布特征。

综上所述，4种模型的拟合效果的优劣顺序，即“有理二次方程式模型”＞“高斯模型”＞“球状模型”＞“指数模型”。

5　结论与讨论

本文选取了琼州海峡潮流50个点的数据，运用泛克里金插值法中4种模型插值进行比较，得出以下结论：

（1）通过交叉验证和点验证的误差分析，由有理二次方程式插值得到的分布结果在平均预测误差、标准化均方根误差和误差范围百分比等指标在4种模型综合比较中最优，同时结合样本点和块金值，有理二次方程式模型更准确地拟合了小范围差异。通过琼州海峡区域的空间插值模型比较，在讨论海洋潮流要素插值模型选择时，首先要确定合理的插值法，在各向异性上进行半变异函数套合，模型验证时不仅要综合多指标的精度，更要考量空间分布与实际接近程度。

（2）克里金插值法本身对步长和步长组的确定、邻域的选择有一定的主观性，同时由于研究海域的范围较大，样本点数目相对较少，海陆边界处没有数据点，是流速值小于100 cm/s时，误差范围百分比较小的主要原因，如在条件允许的情况下，在边缘处增加更多的点，将会提高整体的插值精度。

（3）潮流是一种形成过程受不同物理、化学和生物等因素影响，具有空间异质性的水文要素，同时由于研究资料的限制，本文仅进行单要素直接插值分析，然而影响潮流的因素很多，如在样本中增加其它要素可采用泛克里金或多元回归与克里金相结合的方法进行混合插值分析，进一步提高模型的插值精度，此方法将在今后的研究中探讨。

致谢：琼州海峡区域潮流数据由海洋可再生能源专项资金项目 “海洋能资源勘查与选划成果集成”提供。

［1］Wu He，Yu Huaming，Kuang Liang，et al.Initial Analysis and Assessment of Tidal Current Energy Resource on Qiongzhou Straits［C］//IEEE/MTSOceans’14，Taipei IEEE Xplore，2014：1-6.

［2］张余庆，陈昌春，尹义星，等.江西大潮平均降水量空间插值模型的选取与比较［J］.水土保持研究，2013，20（4）：70-74.

［3］王常森，陶月赞，方必和.淮北平原年降水量空间插值模型的比选［J］.水文，2012，32（2）：49-53.

［4］朱会义，贾绍凤.降雨信息空间插值的不确定性分析［J］.地理科学进展，2004，3（1）：34-41.

［5］汪媛媛，杨忠芳，余涛，等.土壤碳储量计算中不同插值方法对比研究［J］.中国熔岩，2011，12（4）：479-486.

［6］董月娥，刘显傅，张新海，等.基于GIS的海洋光学调查数据空间插值方法研究［J］.海洋技术，2009，6（2）：111-114.

［7］孟庆香，刘国彬，杨勤科.黄土高原降水量的空间插值方法研究［J］.西北农林科技大学学报：自然科学版，2006，34（3）：83-88.

［8］林林，李纯厚，等.海洋浮游植物丰度的空间插值优化［J］.生态学报，2007，7：2880-2888.

［9］林忠辉，莫兴国，李宏轩，等.中国陆地区域气象要素的空间插值［J］.地理学报，2002，57（1）：47-56

［10］钱振华.基于GIS多尺度农林生态环境空间分析及应用研究［D］.上海：上海交通大学，2009.

［11］Kang-tsungChang，陈建飞.地理信息系统导论［M］.北京：清华大学出版社，2008.

［12］刘爱利，王培法，丁园圆.地统计学概论［M］.北京：科学出版社，2012.

［13］汤安国，杨昕，等.地理信息系统空间分析试验教程（第二版）［M］.北京：科学出版社，2012.

［14］侯景儒，等.实用地质统计学［M］.北京：地质出版社，1999.

［15］国家海洋局.GB/T12763.2-2007.海洋调查规范第2部分海洋水文观测［S］.北京：中国标准出版社，2007.

［16］ESRI Arcgis10.2：UseingArcGISGeostatiscal Analyst［R］.2013.

Comparative Study of the Spatial Interpolation Model for Currents in the Qiongzhou Strait Based on GIS

DING Jie，WANG Xiao-yong，WANG Hai-feng，WU He，JIANG Bo，CHEN Li-bo，CHEN Jia-qing，SHI Yong，CAI Xiao-qing
National Ocean Technology Center，Tianjin 300112，China

In order to reflect the spatical distribution characteristics of marine currents in an objective and accurate manner，this paper selects the current velocity data of spring tide in the Qiongzhou Strait.The universal kriging method is used in the exponential，spherical，gaussian and quadratic equation models to fit the precipitaion data after exploring the distribution features of the data.According to cross validation and inspection，the results of the quadratic equation model can be used to obtain better interger effect within the current velocity of spring tide than the other there models.This study provides basis for describing the spatial distribution of the tidal currents in the Qiongzhou Strait and establishing an accurate interpolation model.

Qiongzhou Strait；spatial interpolation；tidal current；universal kriging method

P731

A

1003-2029（2016）04-0074-07

10.3969/j.issn.1003-2029.2016.04.014

2015-07-08

海洋可再生能源专项基金资助项目（GHME2012ZC05）

丁杰（1983-），男，工程师，主要从事海洋专题制图技术与GIS应用研究。E-mail：dingjie831214@foxmail.com