一般耦合6R机器人实时高精度逆运动学算法及应用

蒋坤, 刘承君, 戴义祥, 张峰

(陆军军官学院　a.装甲兵系;　b.训练部, 安徽 合肥　230031)



一般耦合6R机器人实时高精度逆运动学算法及应用

蒋坤a, 刘承君a, 戴义祥b, 张峰a

(陆军军官学院a.装甲兵系;b.训练部, 安徽 合肥230031)

对于一般6R机器人，包括耦合和解耦机械臂，提出一种通用的与常见工业机器人有区别的能够实现实时高精度控制的机械臂逆运动学算法，并且应用在特种多关节机械臂上。基于矩阵多项式理论及其性质，从12个等式方程中重新提取6个独立的等式方程。对多变量等式方程组进行消元后转换成单变量方程，将问题转换为求解单变量方程根的问题，最后利用矩阵多项式的性质将多项式的求根问题转化成为矩阵的特征值求解问题，由此大大降低了求解难度，并且保证了算法的稳定性和精度问题。求解实例表明，提出的该算法能在毫秒级别内得到某种耦合机械臂的所有运动学逆解，并且得到的解能够精确到小数点后11位，从而实现实时高精度控制。

耦合机械臂；矩阵多项式；逆运动学；实时；高精度

0　引　言

自上世纪70年代开始机器人领域的相关专家和学者一直在密切关注和研究一般6R机器人的逆运动学算法问题，研究逆解算法在机器人学研究领域中的意义非常重大。Pieper[1]在1968年最早尝试了将6自由度机械臂逆运动学求解问题转换为单变量多项式问题，提出了解耦机械臂能够得到封闭解。之后Duffy和Derby等[1]相继尝试从6自由多机械臂方程组中提取最简化的特征多项式方程，但是只能达到32次单变量多项式，并且猜想到次数仍可降低。1985年Tsai和Morgan[2]使用多项式连续方法在数值上对非线性方程进行替换，得到了二次多项式方程组的形式。上述研究者也都实践证明了机械臂最多可以得到16组实数逆解问题。在1988年Lee和Liang[1]提出将相同的问题转换成16次单变量多项式问题。1990年和1993年Li以及Raghavan和Roth[3]相继提出了不同的单变量多项式系数计算的过程。1990年Manocha[3]提出了多项式方程的求解方法，将单变量方程组根的求解问题转换成求解矩阵特征值的问题。至此逆运动学问题虽然可以认为基本解决，但是关于如何更加稳定和快速地求解出其所有逆解这一问题至今一直在研究中。

本文中采用以符号推演和数值计算方法为基础的逆解算法，从多项式方程组中消除相关变量，将非线性方程组进行线性组合，将多项式方程等式以矩阵的形式表达出来，最后将求解多项式方程根问题转化成矩阵特征值问题，并且利用特征向量和方程组其他未知数之间的对应关系求解出其它未知数。为了更加方便该算法的应用，依托于MATLAB平台将求解代码程序封装在GUI(图形交互界面)，输入已知量，直观快速的解出未知量。

1　一般6R机械臂运动学方程的建立

基于D-H模型，一般6R机器人运动学方程[4]可以改写成如下形式：

(1)

式中Ai(i=1～6)表示一个连杆相对与下一个连杆间相对关系的齐次变换矩阵，T6表示机器人末端执行器相对于基坐标系之间的相对关系，Ai和T6可分别表示如下：

(2)

ci=cosθi,si=sinθi,μi=sinαi,λi=cosαi，其中θi，di，ai，αi分别表示关节两连杆法线夹角，两连杆相对位置、公共法线距离和扭角参数。di，ai，αi表示机械臂的关节参数，一般6R机器人运动学逆解问题就是在已知di，ai，αi和T6的条件下求解关节变量θi。

由于Dinesh Manocha和John F. Canny[3]构建等式方程的过程复杂，且计算方式繁琐，本文基于位姿矩阵的特征，通过将位姿矩阵分解为位置和姿态分矩阵来重新构建方程中的所需的矢量U,V,W和Y：

(3)

(4)

W=X2Z3X3Q4Q5e

(5)

(6)

式中:

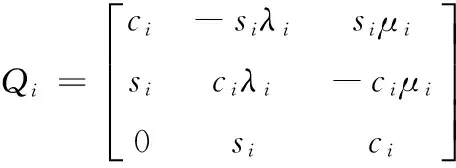
且为正交阵。

由此可以先得到如下两个等式:

U=V

(7)

W=Y

(8)

根据空间向量的投影性质和几何意义，寻找和上述两个矢量式相同的幂乘积(单变量消去法的核心思路)，采用符号运算可以得到以下14个运动学方程。

Ux(θ3,θ4,θ5)=Vx(θ1,θ2)

(9a)

Uy(θ3,θ4,θ5)=Vy(θ1,θ2)

(9b)

Uz(θ3,θ4,θ5)=Vz(θ1,θ2)

(9c)

Wx(θ3,θ4,θ5)=Yx(θ1,θ2)

(9d)

Wy(θ3,θ4,θ5)=Yy(θ1,θ2)

(9e)

Wz(θ3,θ4,θ5)=Yz(θ1,θ2)

(9f)

U·U(θ3,θ4,θ5)=V·V(θ1,θ2)

(9g)

U·W(θ3,θ4,θ5)=V·Y(θ1,θ2)

(9h)

(U×W)x(θ3,θ4,θ5)=(V×Y)x(θ1,θ2)

(9i)

(U×W)y(θ3,θ4,θ5)=(V×Y)y(θ1,θ2)

(9j)

(U×W)z(θ3,θ4,θ5)=(V×Y)z(θ1,θ2)

(9k)

[(U·U)W-2(U·W)U]x(θ3,θ4,θ5)=

[(V·V)Y-2(V·Y)V]x(θ1,θ2)

(9l)

[(U·U)W-2(U·W)U]y(θ3,θ4,θ5)=

[(V·V)Y-2(V·Y)V]y(θ1,θ2)

(9m)

[(U·U)W-2(U·W)U]z(θ3,θ4,θ5)=

[(V·V)Y-2(V·Y)V]z(θ1,θ2)

(9n)

式中下标x,y和z分别表示矢量等式的第一部分、第二部分以及第三部分。为了消去变量，首先应进行变量分离，将等式左边和右边分别提取幂乘积x45、x12，可以得到：

Px45=Qx12

(10)

其中x45=[s4s5s4c5c4s5c4c5s4c4s5c51]T，

x12=[s1s2s1c2c1s2c1c2s1c1s2c2]T。

式中P为元素是θ3线性组合的14×9矩阵，而Q则为14×8常系数矩阵。消元θ1,θ2：

从Q矩阵较为特殊的结构可知，式(10)中的6个等式右边只含有S1和C1，将其中任意两个等式带入到其余四个等式中，如下：

C1x1=n1该式表示上述任意两个等式，其中C1为2×2矩阵，且要求可逆。

C2x1=n2表示余下的四个等式，x1=[cosθ1sinθ1]T。

通过带入消元法消去S1，C1，S2和C2，即可得到只与θ3,θ4,θ5有关的4个等式，写成矩阵形式：

(11)

式中T1表示元素为与θ3有关的4×9矩阵。P2为与上式(10)对应的P矩阵的2×9分块矩阵，同样P4为对应的4×9矩阵，01为2×1零矩阵。

除此之外，对上述剩余的8个等式进行线性变换得到两个等式右边恒为0的等式，通过线性组合消元法将θ1,θ2消去，在Raghavan和Roth[2]构建等式的基础上进一步进行简化修改和验证，重新构造了只和θ3,θ4,θ5有关的两个等式，即：

-λi(U×W)x+ωUy-(r-d1)Wy=0

(12a)

-λi(U×W)y+ωUx-(r-d1)Wx=0

(12b)

其中ω=ozμ6+azλ6，r=-L6az+pz。至此总共得到6个只和变量θ3,θ4,θ5有关的等式方程，列成矩阵形式，得:

T2x45=O2

(13)

式中T2表示元素为与C3或S3线性相关有关多项式的矩阵，O2为6×1零矩阵。

参数代换：

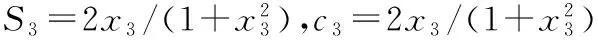
T3(x3)x45=02

(14)

15)

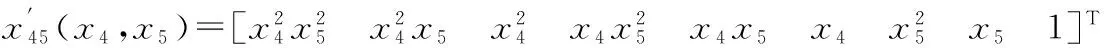
T(x3)x″45(x4,x5)=03

(16)

(17)

式中O63为6×3阶0矩阵，同时矩阵T(x3)可表示为:

(18)

A、B、C皆为12×12阶常系数矩阵。

2　高精度求解

2.1符号推演和数值计算

一般6R机器人方程组求解过程运算量非常之大，且数值计算大多是借助机器浮点运算完成的，由于存在浮点计算的累计误差问题，浮点计算误差不仅仅是位数的问题，且在方程组求解过程中往往存在矩阵条件数大小问题，累计误差可能会直接误导判断的正确性。利用MATLAB软件对上述方程组或者矩阵进行符号预处理，避免了浮点舍入误差的问题。符号运算预处理只需执行一次，每次计算时只需要将数值带入符号运算结果中即可。

2.2矩阵特征值求根

根据线性方程组解性质，可知若式子(16)有解，则有rank(T(x3))<12，即：

det(T(x3))=0

(19)

式子(19)是关于x3的一元16次方程，就单解变量x3的运算量就相当大，计算出x3之后，还需带入线性方程组求解其他变量值，首先浮点计算的累计误差会很大程度上影响解的精度，其次很容易出现增根、漏解的情况，更重要的是该计算方式只能在线下求解，且计算时间较长，总言之无法实现实时高精度。与Raghavan和Roth等[2]采用的较为复杂繁琐的计算方法不同，利用矩阵特征值求解的方法能较好的解决上述问题。

若A矩阵可逆，将式(18)两边同时左乘A-1，得：

(20)

其中E为单位阵，根据矩阵多项式理论可知式(1.19)的根对应如下矩阵M的特征值：

该矩阵的特征值x3所对应的特征向量即为x″45(x4,x5)，即可求解出x4和x5，将求解出来的三个未知数带入式(1)求解出x1和x2，最终再求解出x6。

然而在很多情况下，A矩阵的条件数是非常大的，即A矩阵接近不可逆，如此就无法转换为可以求解的莫尼矩阵多项式，因此利用简单的元素线性代换法[5]，将A矩阵调整为可逆。将式(18)中的x3线性替换成：

(21)

2.3提高求解精度

每个特征值对应的矩阵条件数的大小各不相同，即求解精度也各不相同。如果需要进一步提高求解精度，将最初始计算出来的数值利用牛顿迭代法进行一到两次迭代可以进一步提高求解精度(前提是要形成局部收敛情况)。

3　算法应用于某种型号耦合机械臂

依托于MATLAB数学计算软件，选择具有代表性的6个旋转自由度关节的某种内窥机械臂作为求解实例，验证算法的可行性和有效性。关节参数如表1与图1所示。

表1　机械臂D-H参数

表1中θ为两连杆法线夹角，d为两连杆相对位置，a为公共法线距离，α为扭角参数。

图1　运动学研究软件界面

将机械臂模型导入至托卡马克真空室内部，将每个关节旋转至一定的角度(例θ1=60°，θ2=15°，θ3=20°，θ4=25°，θ5=25°，θ6=20°θ1=60°，θ2=15°，θ3=20°，θ4=25°，θ5=25°，θ6=20°)，测量机械臂末端执行器末端位姿矩阵(假设为目标点位姿)，可表示为:

(22)

在MATLAB软件中以符号运算为基础进行运算，之后带入12位精度的各关节参数和目标点的位姿，最终求解出各关节转角。

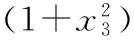
表2　求解结果

实验数据表明，该算法解出的第三组角度值相对理论值能够精确到小数点后11位，求解全过程充分验证了算法的稳定性、实时性和精度，能够完全满足一般6R机器人的实时高精度控制的需要，满足了对某些必须使用耦合机械臂上的应用。

4　结束语

(1) 根据矩阵多项式理论和矩阵性质构建6个相互独立的等式方程，简化了计算过程的复杂程度。

(2) 通过符号运算避免了一般浮点运算带来的累计误差从

而提高算法的精度，并且通过转换成求解矩阵特征值的途径提高了算法的稳定性和效率。

(3) 通过MATLAB自带的GUI界面，将算法过程转换成程序语言并将其封装在其内部，将已知量输入之后可以在毫秒级别快速得到高精度解，将一般6R机器人逆运动学算法成功应用于AIA多关节机械臂，满足了实时高精度控制的需要。

[1] JORGE ANGELES.Fundamentals of robotic mechanical system. theory, methods and algorithms, second edition[M].New York:Springer,2003.

[2] MADHUSUDAN RAGHAVAN, BERNARD ROTH.Kinematic analysis of the 6R manipulator of general geometry[J].Journal of Mechanical Design,1990,115(3):502-508.

[3] DINESH MANOCHA,JOHN F CANNY.Efficient inverse kinematics for general 6R manipulators[J]. IEEE Transactions on Robotics and Automation, 1994,5(10):648-657.

[4] 蔡自兴.机器人学[M].北京：清华大学出版社，2000.

[5] 刘松国,朱世强,王宣银. 基于矩阵分解的一般6R机器人实时高精度逆运动学算法[J].机械工程学报，2008，44(11):304-309.

Algorithm and Application of Real-time Highly-accurate Inverse Dynamics of General Coupling 6R Robots

JIANG Kuna, LIU Cheng-juna, DAI Yi-xiangb, ZHANG Fenga

(a. Department of Armored Reconnaissance, b. Training Division, Academy of Army Officer, Hefei Anhui 230031, China)

For general 6R robots including coupling and decoupling robot arms, this paper presents an inverse dynamics algorithm of the robot arm with real-time and highly accurate control which differs from common industrial robots, and applies it to special robot arms with multiple joints. Based on the theory and property of matrix polynomials, 6 independent equations are drawn from 12 equations. Then, multi-variable equation groups are transferred into a single-variable equation through element elimination, so that we are now faced with the problem of finding the root of the single-variable equation. Finally, using the properties of the matrix polynomial, we transform the problem of extracting the root of a polynomial to finding the proper value of a matrix, thus making the solution much easier and ensuring the stability and accuracy of the algorithm. Solution examples indicate that the proposed algorithm can obtain all inverse kinematics of a specific coupling robot arm on the ms level, and the solution can be correct up to 11 decimal places, thus realizing real-time and highly accurate control.

coupling robot arm;matrix polynomial;inverse kinematics; real time;high accuracy

10.3969/j.issn.1000-3886.2016.02.031

TP242

A

1000-3886(2016)02-0102-04

蒋坤(1981-)，男，安徽涡阳人，讲师，硕士，电气工程专业方向。

定稿日期: 2015-09-16