遗传优化同步电机分数阶PID预测函数励磁控制器

郁振波， 郭伟1,， 夏友亮， 陈琛

(1.江苏省大气环境与装备技术协同创新中心,江苏 南京　210044;2.南京信息工程大学 信息与控制学院,江苏 南京　210044)



遗传优化同步电机分数阶PID预测函数励磁控制器

郁振波2， 郭伟1,2， 夏友亮2， 陈琛2

(1.江苏省大气环境与装备技术协同创新中心,江苏 南京210044;2.南京信息工程大学 信息与控制学院,江苏 南京210044)

为提高同步电机励磁调节器的控制性能，提出一种基于遗传算法优化同步电机分数阶PID预测函数励磁控制器的设计方法。将同步电机的励磁系统进行线性化处理，在分数阶系统理论的基础上用预测函数控制推导出同步电机励磁调节器的分数阶传递函数模型，并根据所得到的系统性能综合指标评价函数再用遗传算法对分数阶PID预测函数控制器的参数进行优化整定。经仿真实验验证，与传统分数阶PID控制和预测函数控制相比，不仅减小了调节时间，增强了系统抗干扰能力，无稳态误差。并且在参数整定方面，遗传算法的收敛速度和寻优能力也明显优于模糊控制和粒子群算法。

PID；预测函数控制;同步电机;遗传算法;参数整定

0　引　言

同步电机励磁控制系统是电力系统控制的重要组成部分，其运行情况影响整个系统的性能[1]。同步电机励磁系统的动、静态特性很大程度上决定于励磁调节器，控制方法的优化即对同步电机励磁调节器的设计便成了整个控制系统的关键所在。

文献[2]中采用带电力系统稳定器(power system stabilizer，简称PSS)环节的PID和线性最优磁控制器(linear optimisum excitation controller，简称LOEC)，改善了电力系统阻尼特性和小干扰稳定性，但是该控制器一方面控制参数需要通过实验方法整定，工作量庞大，且人工整定很难得到最佳控制效果。文献[3]中采用非线性励磁控制器，提高了电力系统在大干扰下的稳定性，但仍依靠设计者经验，且算法设计和数学过程极为复杂。文献[4]中的自适应励磁控制器一定程度上改善了控制性能，但是算法复杂，计算量大。针对这些缺陷，文献[5]提出智能励磁控制器，如模糊控制、粒子群算法、遗传算法(Genetic Algorithms，简称GA)等。

本文提出一种基于GA优化同步电机分数阶预测函数(Fractional Order Predictive Function Control，FOPIDPFC)励磁控制器。该控制器将同步电机励磁系统的数学模型扩展为一个分数阶系统[6]，利用基于偏差调节的思想改写预测函数控制的目标函数，使之不仅具有PID控制结构简单、鲁棒性强的特点，同时可以预测系统未来输出。由于新参数的引进和算法本身复杂度的提高，本文采用遗传算法对参数进行优化。经仿真实验验证，本文提出的控制方法兼具FOPID和PFC算法优点，且相比于模糊算法和粒子群算法，收敛速度更快，寻优能力更强。

1　励磁控制系统

励磁系统是由励磁控制部分、同步发电机及检测单元共同组成的反馈控制系统。励磁控制部分包括励磁功率单元和励磁调节器。该调节器是由放大环节、励磁环节及检测环节构成的一个闭环控制系统，其结构框图如图1所示。

图1　同步电机励磁调节系统示意图

分数阶开环传递函数结构形式可在传统传递函数的基础上改写为[7]：

(1)

式中K为放大系数；T为时间常数；αA，αE，αM分别分数阶系统的三个环节的阶次。

2　基于GA的FOPIDPFC励磁控制器

2.1FOPIDPFC励磁控制器

分数阶模型相比整数阶系统模型可更准确地描述实际工程系统动态性能，提高对系统动态性能的表述、分析和控制能力[8]。FOPIDPFC将FOPID与PFC相结合，具有kp,ki,kd,λ,μ等多个可调参数，控制器的设计更加灵活。

由增量式FOPID控制器和预测函数的目标函数可得FOPIDPFC目标函数的向量形式：

(2)

式中Δe=Δμg-Δd；e=μg-d；ej=μjg-dj；Q和R为控制量的加权矩阵；U为控制量矩阵。

(3)

控制量：

(4)

其中fk(0)=[fk1(0),fk2(0),…,fkJ(0)]T,q-1为后移算子。

2.2基于GA的FOPID励磁控制器参数优化策略

2.2.1系统性能综合指标评价函数的确定

图2　控制系统的控制框图

遗传算法是一类借鉴生物界自然选择和自然遗传机制的随机搜索算法。具有对问题搜索上的全局性、计算上的内在并行性、处理上的灵活性以及很好的鲁棒性(见图2)。

FOPIDPFC励磁控制器系统输入如下：

(5)

本文采用误差的绝对值与时间乘积的积分和调试时间的加权和作为最终的系统性能综合指标评价函数[9]，即:

(6)

式中w1，w2为权值；t为调节时间。该系统性能综合指标评价函数即为最终基于GA的FOPIDPFC励磁控制器的目标函数。

2.2.2基于GA的FOPIDPFC参数优化

算法的具体步骤如下：

Step 1参数编码和译码。本文采用格雷码编码方式代替传统二进制编码，克服其二进制编码存在海明距离的缺陷。

Step 2种群初始化。本文在经验的基础上，将五个参数范围尽可能取得大，精度保留四位有效数字。

Step 3适应度函数。由于J取值越小，系统性能越好，而遗传算法的适应度函数是函数值越大，个体对环境的适应能力越强，所以要对目标函数进行改造，将求极小值问题转化为求极大值问题，所采用的变化方法为：

(7)

式中Cmax为一个相对比较大的数，一般选取一个比进化到当代为止的最大的目标函数还大的值，本文取值为10。

Step 4选择操作。本文采用轮盘赌式选择法。

Step 5交换操作。本文采用多点交叉和均匀交叉，且逐步增加均匀交叉的概率。

Step 6变异操作。本文的变异是指改变数字串中的某一位，变异位由随机函数产生的随机数来决定。

3　励磁系统仿真分析

3.1FOPIDPFC励磁控制器的仿真分析

通过MATLAB仿真，得到FOPID，PFC，FOPIDPFC三种不同励磁控制方法下的仿真曲线。通过经验法选取的参数如下，其中FOPID的参数kp=100、ki=0.2、kd=4.7、λ=2.8 、μ=0.08；PFC的参数P=5、M=5；FOPIDPFC的参数kp=50、ki=7、kd=35、λ=0.5 、μ=0.8、P=5、M=5。

从图3可知，FOPID的超调量为38%，PFC为0.5%，FOPIDPFC的超调量在实际控制中可以忽略不计。FOPID的稳态误差为0.38%，PFC和FOPIDPFC的稳态误差可以忽略不计。5 s时加入阶跃扰动，FOPID产生13%的波动，1.02 s后恢复稳定，PFC产生11%的波动，0.08 s后恢复稳定，FOPIDPFC产生6.5%的波动，0.03 s后恢复稳定。综上，FOPIDPFC励磁控制器的性能显著优于前两者。

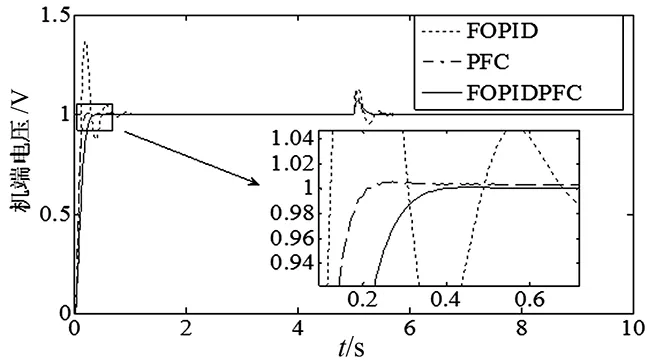
图3　励磁系统响应曲线

3.2基于GA的FOPIDPFC励磁控制器仿真分析

GA优化FOPIDPFC励磁控制器参数设置：遗传代数eranum=100，种族大小popsize=60，交换概率pc=0.8，变异概率pm=0.1，倒位概率pin=0.15。变量kp,ki,kd,λ,μ的取值范围分别为0～200、0～200、0～200、0～20、0～20(且保留到小数点后4位有效数字)。适应度权值w1=0.5，w2=0.7。所需时间为28分钟4.66 50秒。

根据经验法[10]调节的FOPID预测函数励磁控制器模型为:

(8)

经遗传算法优化后，系统最佳FOPIDPFC励磁控制器模型为:

(9)

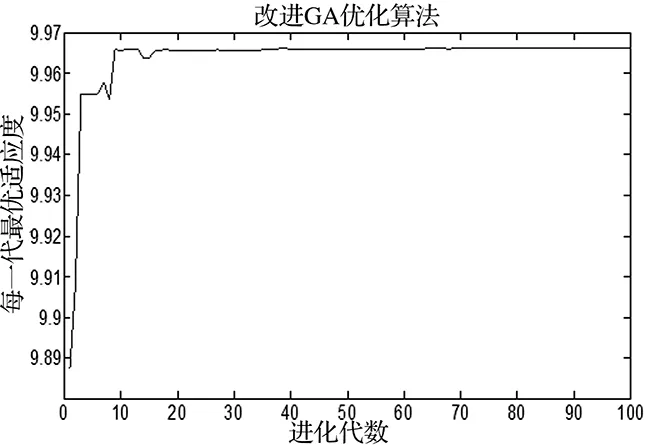
图4　进化代数与适应度的关系

图5　励磁系统响应速度曲线

图6　励磁系统稳态误差曲线

从图4可看出，GA算法适应度变化迅速，在5代左右陷入局部最优，即早熟现象，在10代左右达到最优。因为变异算子的存在，使其有一定的扰动几率，大大提高了结果的准确性和可靠性，最终在36代达到稳定，之后基本保持不变。

从图5可知GAFOPIDPFC响应速度最快，PSOFOPIDPFC次之，FuzzyFOPIDPFC则相差较多。从图6可知GAFOPIDPFC稳态误差基本等于0，而另外两种算法优化控制器都有少许的稳态误差，陷入了局部最优。由图7可知受到小干扰后，GAFOPIDPFC能最快达到稳定，不仅体现出GA算法相比于其他智能算法的优越性，更展现了FOPIDPFC控制策略良好的控制效果。表1给出了三种方法优化分数阶PID预测函数的性能指标。

通过对比分析，GA算法优化FOPIDPFC不仅比传统意义上的FOPID和PFC具有更好的动态性能，而且同比另外两种主流智能算法，遗传算法具有更强的寻优能力。

表1　FOPIDPFC控制器性能指标

图7　励磁系统抗扰动对比曲线

4　结束语

本文将同步电机励磁控制系统扩展为分数阶形式，提高了对系统模型的描述能力。在此基础上将分数阶PID控制与预测函数控制相结合，得到一种兼具PID控制及预测函数控制优点的新型控制算法。该算法具有五个可调参数，提高系统灵活性的同时，也大大增加了控制难度。针对这一问题进一步提出一种利用遗传算法整定FOPIDPFC参数的方法。经仿真实验表明，该方法不仅可以使FOPIDPFC算法得到优越的控制效果，同时也比PSO算法和模糊控制拥有更强的寻优能力。具有一定的理论与实际价值。

[1] RAY P S, DUTTAGUPTA P B, BHAKTA P. Coordinate PSS design using both speed and electric power[J]. IEEE Proceedings of Generation,Transmission and Distribution,1995.142(5):503-510.

[2] M J BASLER, R C SCHAEFER. Understanding power system stability[J]. Pulp and Paper Industry Technical Conference, Conference Record of Annual.2007:24-28.

[3] GIUSEPPE F, MARIO R. Nonlinear control design for excitation controller and power system stabilizer[J]. Control Engineering Practice, 2011.19(3):243-251.

[4] 陈欢, 季海波, 王冰，等. 同步励磁发电机鲁棒自适应控制[J]. 中国科学技术大学学报, 2004,34(2): 206- 212.

[5] 李文, 欧青立,沈洪远，等. 智能控制及其应用综述[J]. 重庆邮电学院学报:自然科学版, 2006,18(3): 376-381.

[6] 赵春娜, 潘峰, 薛定宇. 分数阶H_∞控制器设计[J].东北大学学报：自然科学版，2006,27(11):1189-1192.

[7] 姚舜才,潘宏侠.粒子群优化同步电机分数阶鲁棒励磁控制器[J]. 中国电机工程学报, 2010,30(21): 91-97.

[8] 王东风,王晓燕,韩璞. 锅炉-汽轮机系统的分数阶控制器设计[J]. 中国电机工程学报, 2010,30(5): 113-119.

[9] 郭伟, 韩丹丹,徐金成，等.基于粒子群优化的分数阶PID预测函数参数整定[J]. 控制工程, 2014,21(1):70-73.

[10] 郭伟, 倪家健，李涛,等. 基于时域的分数阶PID预测函数励磁控制器[J]. 仪器仪表学报, 2011,32(11): 2461-2467.

Fractional-order Prediction Function Excitation Controller Based on the Genetically Optimized Synchronous Motor

YU Zhen-bo2, GUO Wei1,2, XIA You-liang2, CHEN Chen2

(1.Jiangsu Collaborative Innovation Center for Atmospheric Environment and Equipment Technology, Nanjing Jiangsu 210044, China;2. School of Information and Control, Nanjing University of Information Engineering, Nanjing Jiangsu 210044, China)

To improve the control performance of the excitation regulator of the synchronous motor, this paper presents a method for designing the fractional-order PID prediction function excitation controller based on the genetically optimized synchronous motor. The excitation system of the synchronous motor is linealized. Based on the theory of the fractional-order system, a fractional-order transfer function model is derived through prediction function for the excitation regulator of the synchronous motor. Then, on the basis of the acquired comprehensive index evaluation function for the system performance, genetic algorithm is used to optimize the parameters of the fractional-order PID prediction function controller. Simulation results show that the setting time is reduced and the anti-interference capability is enhanced when compared with traditional fractional-order PID control and prediction function control, and no steady-state error occurs. Furthermore, in the aspect of parameter setting, the convergence rate and optimization ability of the genetic algorithm are obviously superior to those of fuzzy control and particle swarm algorithm.

PID; predictive functional control; synchronous motor; genetic algorithm; parameter setting

江苏省高校大学生创新创业项目(201410300034Z)；国家自然科学基金(61473334)

10.3969/j.issn.1000-3886.2016.02.002

TP273

A

1000-3886(2016)02-0004-03

郁振波(1995-)：男，江苏泰州人，学士，主要从事预测控制在励磁系统系统中的应用。郭伟(1960-)：男，安徽巢湖人，教授，硕士生导师，主要从事预测控制，电机控制、励磁系统控制技术等研究工作。

定稿日期: 2015-05-18