直击点与圆的位置关系

张卫

直击点与圆的位置关系

张卫

毕达哥拉斯曾经说过：“一切立体图形中最美的是球形，一切平面图形中最美的是圆.”同学们，当你开始“圆”这一章的学习时就进入了一个神奇美丽的世界，让我们从学习点与圆的位置关系开始吧！

一、概念释疑

认真的你一定会注意到，在我们的书本上对“圆”给出了两种不同的定义：

1.把线段OP绕着端点O在平面内旋转一周，端点P运动所形成的图形叫做圆.

2.圆是到定点的距离等于定长的点的集合.

对于第一种解释大家应该很容易理解，对于第二种定义同学们可能就不太好理解了.通俗地讲集合就是由具有同一属性的对象汇总成的集体，第二种定义的意思就是：圆，只有一个圆心，圆心到圆上各点的长都相等，并且到圆心的距离等于定长的点都在这个圆上.

二、概念拓展

如果我们在平面上画一个圆，我们可以知道平面内的点与这个圆存在三种位置关系：（1）点在圆上；（2）点在圆内；（3）点在圆外.

由此我们还可以得出两个结论：

1.圆的内部可以看作是到圆心的距离小于半径的点的集合.

2.圆的外部可以看作是到圆心的距离大于半径的点的集合.

三、例题的拓展

苏科版《数学》教科书第39页尝试与交流：

如图1，线段PQ=2cm.

（1）画出下列图形：

到点P的距离等于1cm的点的集合；到点Q的距离等于1.5cm的点的集合.

（2）在所画图中，到点P的距离等于1cm，且到点Q的距离等于1.5cm的点有几个？请在图中将它们表示出来.

（3）在所画图中，到点P的距离小于或等于1cm，且到点Q的距离大于或等于1.5cm的点的集合是怎样的图形？把它画出来.

图1

【解析】（1）到点P的距离等于1cm的点的集合是以P为圆心、1cm长为半径的圆，到点Q的距离等于1.5cm的点的集合是以Q为圆心、1.5cm长为半径的圆，如图2-a；

（2）满足条件的点有两个，为（1）中两圆的交点M、N，如图2-b；

（3）由前面的概念可知这样的点既在⊙P内或⊙P上又得在⊙Q外或⊙Q上，即为如图2-c的阴影部分（包括边界）.

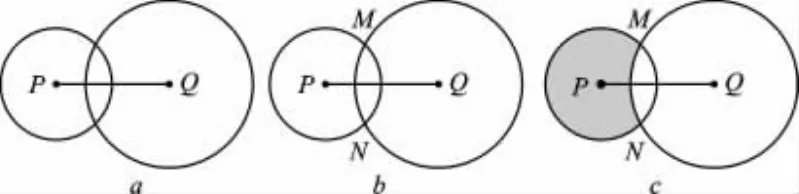
图2

变式1圆心位置、半径大小都确定

如图3，在Rt△ABC中，∠ACB=90°，BC=4，∠A=30°，E、F分别为AB、AC的中点，以B为圆心，BC为半径画圆，试判断点A、C、E、F与⊙B的位置关系.

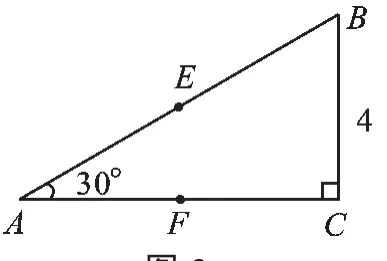
图3

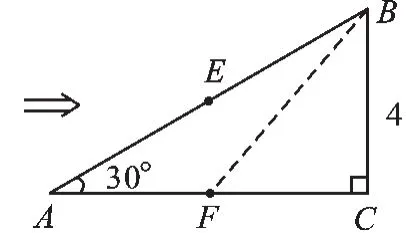
图4

【解析】在Rt△ABC中，∠A=30°，BC=4，所以AB=8>4，则点A在⊙B外；很明显，点C在⊙B上；所以点E在⊙B上；连接BF，在Rt△BCF中，BF>BC，所以点F在⊙B外.

【点评】现在要判定平面内一点与圆的位置关系，除了通过画图，还可以通过比较该点到圆心的距离与半径的大小来判定，而后者以后会用得更多些.

变式2圆心位置不变，半径改变

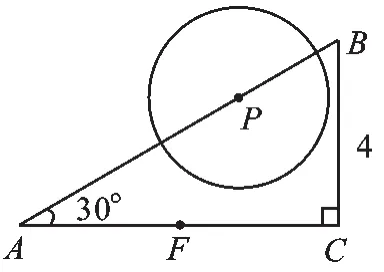
在Rt△ABC中，∠ACB=90°，∠A=30°，BC= 4.以B为圆心、r为半径画圆，当r在什么范围时，点C在⊙B内，点A在⊙B外.

【解析】要使点C在⊙B内，r>BC=4；要使点A在⊙B外，r

变式3圆心位置改变，半径不变

如图5，在Rt△ABC中，∠ACB=90°，BC=4，∠A=30°，点F为AC中点，点P为AB上一动点，以P为圆心、2为半径作⊙P，当点P由B→A以1个单位每秒的速度运动（点P到A时运动停止）过程中，点F在⊙P内有多少时间？

图5

图6

变式4圆心位置、半径大小都改变

如图7，在Rt△ABC中，∠ACB=90°，BC=4，∠A=30°，点F为AC中点，点P为AB上一动点，当点P由B→A以1个单位每秒的速度运动时（点P到A时运动停止），以P为圆心的圆的半径也由0开始以1个单位每秒的速度变大.在这个过程中，点F在⊙P内有多少时间？

图7

图8

同学们有没有发现上面的例子都是万变不离其宗——紧紧围绕着点与圆的位置关系，所以平时大家多积累一定能有更多收获！

（作者单位：江苏省常州市新北区龙虎塘中学）